航空器供油问题中完全逆序类中的多项式时间可解类
2019-02-15王丽丽崔晋川
王丽丽, 崔晋川
(中国科学院 数学与系统科学研究院,北京 100190)
0 引言


1 航空器供油问题的性质
1.1 数学模型[2]
设有n架飞机{V1,V2,…,Vn},飞机Vi(i=1,2,…,n)载油量为ai(L),耗油率为bi(L/Km),按照退出飞行的顺序σ,第i架退出飞行的飞机已经飞行的距离表示为
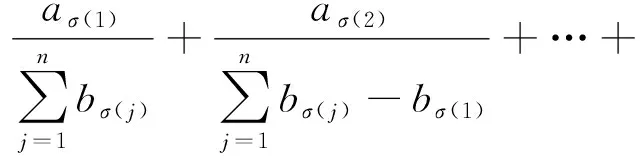
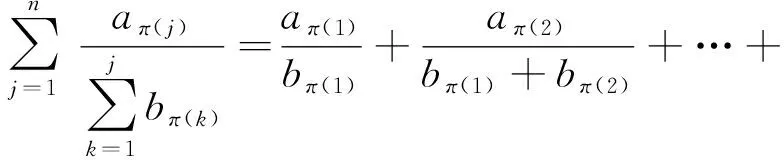
航空器供油问题的示意图如图1所示,O为出发点,Aπ(i)为飞机Vπ(i)行驶的最远点(i=1,2,…,n),同时Aπ(1)是n架飞机在该排序下行驶的最远点。其中xπ(i)表示Vπ(i)比Vπ(j+1)多行驶的距离(i=1,2,…,n-1),xπ(n)表示Vπ(n)行驶的距离。

图1 架飞机的飞行顺序及飞行距离示意图
Vásquez等[5]把该问题看做一类形如minΣωjf(Cj)的特殊的工件排序问题,因为


1.2 航空器供油问题最优解的必要条件
梁莉莉用邻位对换的方法得出了航空器供油问题的最优解的必要条件[12],描述如下:

下文提到的最优排序均指飞机飞行距离由远及近的排序。
1.3 航空器供油问题最优解的必要条件

2 航空器供油问题的唯一解类
定理1给定属于“完全逆序类”的n架飞机{V1,V2,…,Vn},其中Vi的载油量为ai(L),耗油率为bi(L/km),若满足条件:
则该航空器供油问题满足引理1的解只有一个,最优排序为π=(1,2,…,n)。

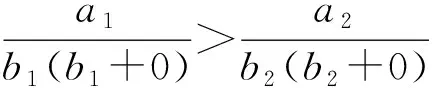
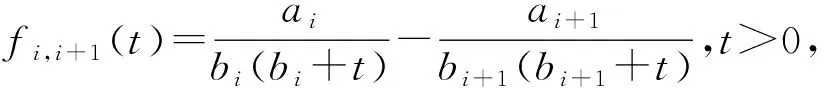
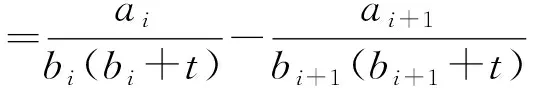




下证除排序π=(1,2,…,n)以外,其他排序都不满足引理1。
设排序θ=(θ(1),θ(2),…,θ(n))为不同于π=(1,2,…,n)的任意排序,下证相邻两架飞机不满足引理1。
由题意,排序θ中必存在i,i∈(1,2,…,n),使得θ(i)>θ(i+1),下证该相邻两架飞机不满足引理1。
考虑函数

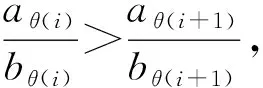
根据条件
故有gθ(i),θ(i+1)(B)<0,即排序θ不满足必要条件。
综上所述,满足必要条件的排序只有一种,即为π=(1,2,…,n)。

证明设最优排序为π=(π(1),π(2),…,π(n))。
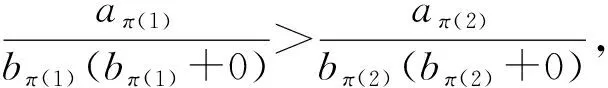
下面证明当π(1)选定以后,其余n-1架飞机的排序是唯一确定的。
令π(1)=k,(k∈N,k≠n),则π=(k,n,n-1,…,k+1,k-1,…,1)。
下证该排序满足引理1。
当i≥2时,构造函数
化简得

下证gπ(i),π(i+1)(t)>0,(i=2,3,…,n-1)成立。
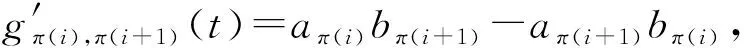
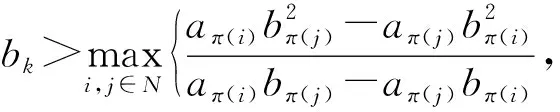
即排序π=(k,n,n-1,…,k+1,k-1,…,1)满足引理1。
设最优排序表示为π=(bk,A),k∈N,k≠n,A为排序子序列。
下证除A=(n,n-1,…,k+1,k-1,…,1)外,其他排序都不满足引理1。
假设排序θ=(θ(1),θ(2),…,θ(n))为任意不同于A的排序,下证该排序不满足引理1。
由题意,排序θ中必存在m,m∈{1,2,…,n-2},使得θ(m)<θ(m+1)>,下证该相邻两架飞机不满足引理1。
考虑函数


综上所述,该类问题的最优解,采用枚举法有n-1种情况。
故该类航空器供油问题可在多项式时间内求得最优解。
3 实例分析
例1假定机队共有10架飞机,每架飞机所携带的燃油量ai(L)与耗油量bi(L/km)如下表。求该机队的最远行驶距离。
解在该实例中,a/b递增排列,a/b2递减排列,属于“完全逆序类”,由于该实例满足本文定理的条件:
有512.3<740,所以最优排序为

1⟹2⟹3⟹4⟹5⟹6⟹7⟹8⟹9⟹10
4 结论
文中主要研究了航空器供油问题的“完全逆序类”,“完全逆序类”具有指数时间复杂度。对大部分的难问题,人们通常用最坏情况的计算复杂度来刻画其难度,“完全逆序类”是航空器供油问题中最难解的一类,当规模较大时,计算时间较长,人们往往放弃利用精确算法寻找精确解,转而利用启发式算法或近似算法,但是按照本文定理的结论,“完全逆序类”中也存在实例可以在非常短的时间内求得精确解。本文通过对其数据特征的分析,发现其中也存在着多项式时间可解的特殊结构。定理1描述一类特殊的航空器供油问题,该类问题在求解前即可判定其满足最优解必要条件的排序是唯一的。定理2所描述的一类特殊结构也可在多项式时间内求得最优解。
