遗传算法结合差分法求解某受压杆件临界荷载①
2019-02-15高守栋
吴 珂, 高守栋
(1.安徽建筑大学土木工程学院,安徽 合肥 230601;2.广州大学土木工程学院,广东 广州 510006)
0 引 言
对受压构件稳定性分析方法有:中性平衡法、微分方程法、能量法、变分法、势能驻值法、差分法、有限单元法等[1]。
差分法又称差商法,是一种用差商近似导数的方法,分为向前差商型微分公式、向后差商型微分公式和中心差商型微分公式[2]。将一端固定一端铰接的轴心受压杆件划分为n段,运用差分公式使得微分方程转化为代数方程的形式,从而将微分方程的问题简化为代数方程组的问题。但是,该方程组为含有一个未知量的代数方程组,若使用传统方法,求解代数方程组工作量大,求解一元高次多项式的根也很困难[1]。
受一篇文章的启发[3],在差分法的基础上,先使用MATLAB求出代数方程组的解,该解是含有一个未知量的高次多项式。再使用人工智能算法中的遗传算法求解一元高次多项式的最小正根,从而得到一端固定一端铰接的轴心受压杆件的临界荷载Pcr。差分法结合遗传算法求Pcr,求解思路清晰,过程简单。
1 代数方程组的求解[1]
1.1 n=2时,代数方程组的求解
函数y=f(x)的图形见图1,纵坐标y(i-2h)、y(i-h)、y(i)、y(i+h)、y(i+2h)分别表示 函数f(x)在i-2h、i-h、i、i+h、i+2h处的函数值,h为各相邻点间的距离,于是有二阶导数的差分公式
(1)
四阶导数的差分公式为
(2)
下端固定、上端铰接的轴心受压杆件图见图2,其四阶微分方程为
(3)
将公式(2)和(3)代入(1)得到任一点i的差分方程为
ui+2h-4ui+h+6ui-4ui-h+ui-2h+
(4)
将杆件分为两段,其图形见图3,此时n=2,i=1,h=L/n=L/2,由公式(4)和边界条件可得方程组
u0=0
u2=0
u-1-u1=0
u1+u3=0
(5)
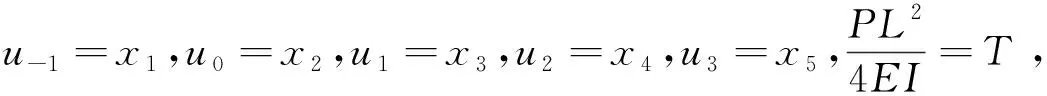
(6)
令Ax=b,其中
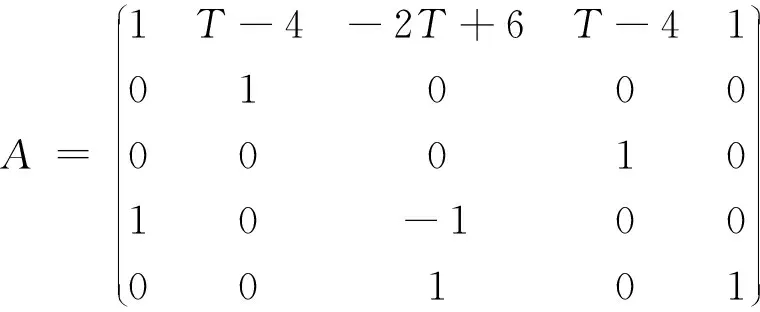
A是一个5阶方阵,且含有未知量T。为了使得Ax=b有非零解,则必有A的行列式为0,det(A)=0 ⟹6-2T=0。
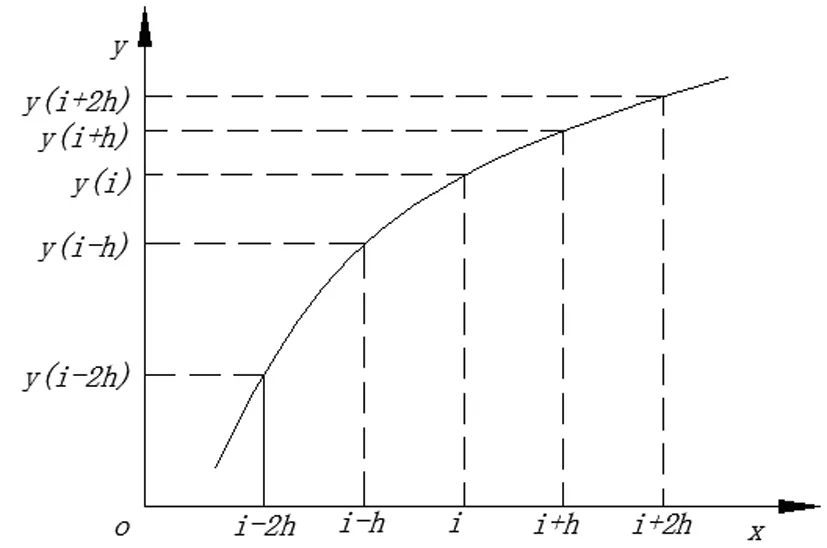
图1
1.2 n>2时,代数方程组的求解
当n>2,表示杆件划分的段数≥3,此时矩阵A的阶数≥6,如果采用手算则计算量很大,且容易出错。采用MATLAB中的函数det(A)[6],会返回A的行列式的值,能够快速准确的计算A的行列式。调用的代码为f=det(A),即将函数det(A)返回的值赋予f。n=3时,方程组Ax=b的形式为:
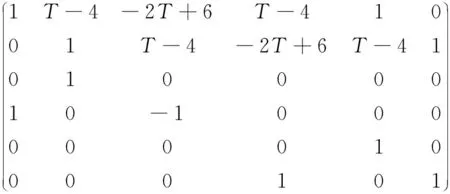
(7)
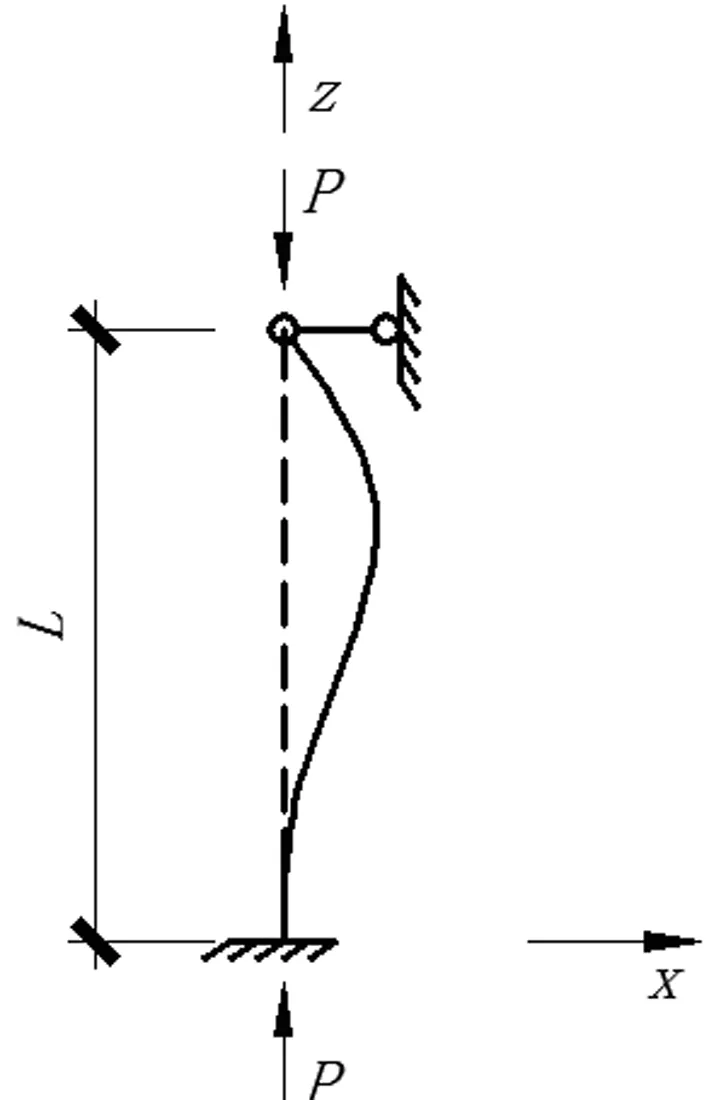
图2
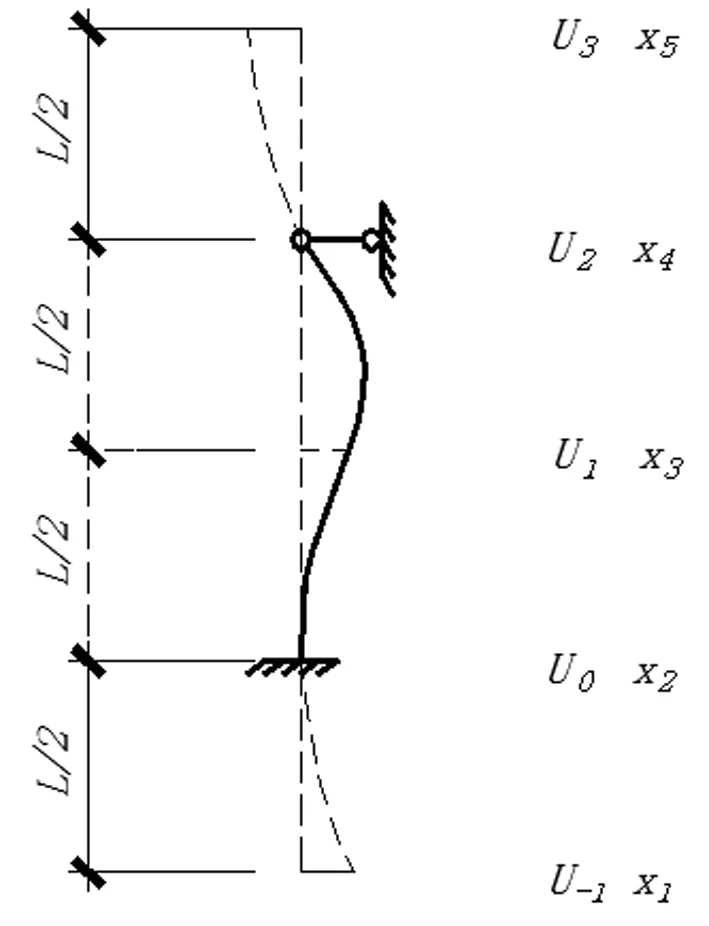
图3

表1 矩阵A行列式的值
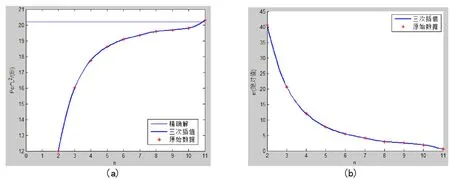
图4
2 遗传算法求解一元高次多项式的根
2.1 遗传算法简介
1975年,Michigan大学的J. H. Holland对遗传算法进行了系统的研究,并发表论文[7]阐述了遗传算法的基本理论和基本方法。De Jong是Holland的学生,他在其老师研究的基础上,使用计算机做了大量数值实验并得出具有指导意义的结论[8]。在计算机技术快速进步的80年代,遗传算法在工程优化领域、经济预测领域、机器学习等领域得以成功应用。90年代至今,遗传算法已经形成一套完整的体系,并随着人工智能技术的发展不断完善。
2.2 运用遗传算法求T[9]
通过GUI使用MATLAB遗传算法工具箱[10],版本为2014A,对表1中关于T的多项式进行求解。
当n=2时,f(T)=6-2T。由于ga函数只解决最小值的问题,所以直接使用f(T)=6-2T作为目标函数求T是不可取的,必须要对f(T)作适当变换。这里采用加绝对值的方法,将求解f(T)=6-2T=0的根的问题转化为求g(T)=|f(T|)=|6-2T|的最小值的问题,求得T的值为3。
当n=3时,f(T)=-3T2+16T-19,g(T)=|-3T2+16T-19|。函数f(T)有两个根,使用ga函数能够把所有的根求出。随着n的增大,f(T)的根会越来越多,要求的是f(T)的最小正根,因此需要对ga函数施加约束。约束条件为T2,求解的结果T=1.78。需要注意的是,n不同则约束条件也不同,这里用g(T)的函数图像来修正约束条件。n=2,3,…,10时T的值见表2。
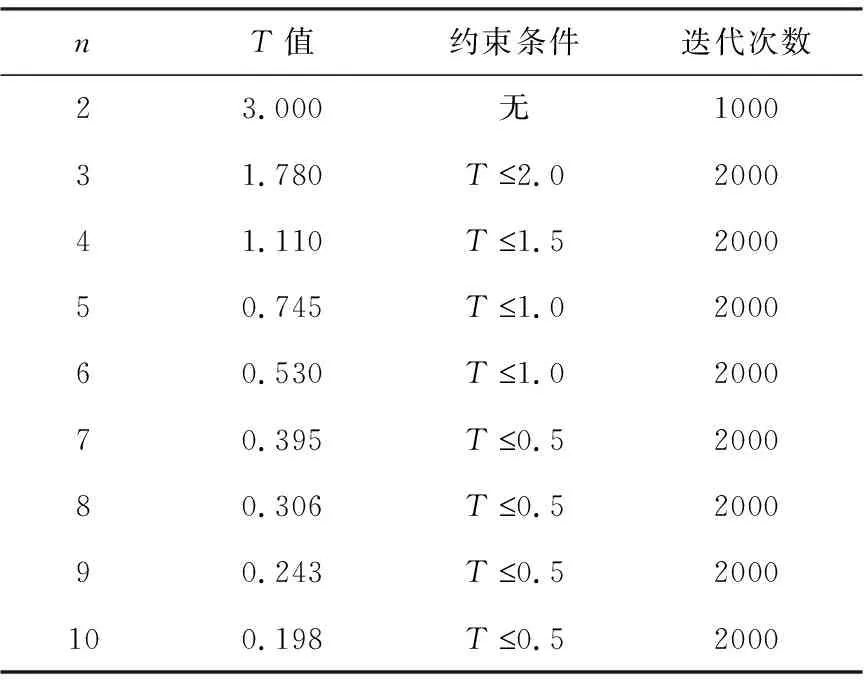
表2 T值
3 临界荷载Pcr及误差计算[2]
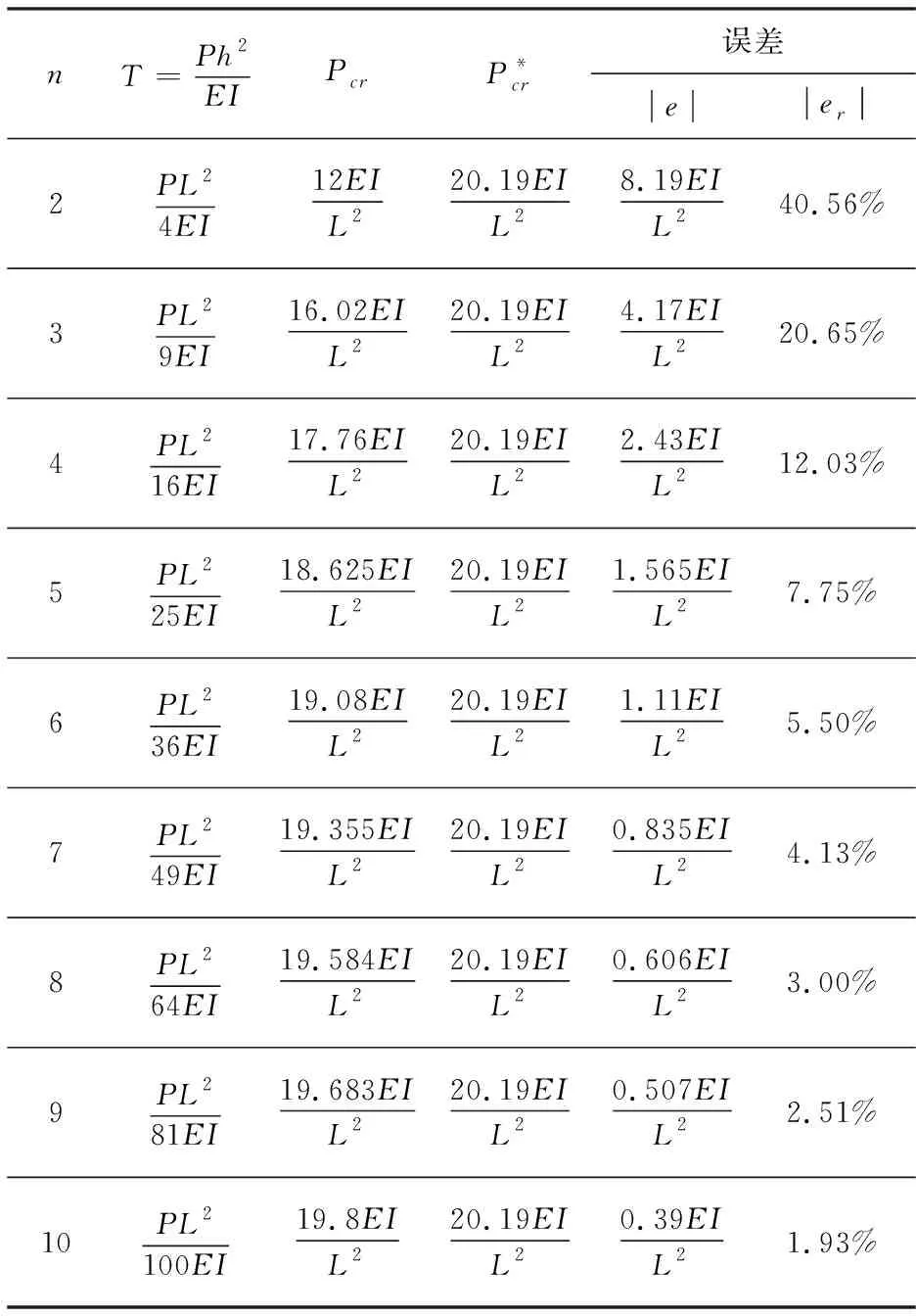
表3 Pcr值及误差值
4 里查森外推法[1]
分析表3可知,当n大于5时,|er|的收敛速度显著降低,出现工作量增加但效果不佳的情况。为了减少计算工作量的同时快速减小误差,使用里查森外推法来计算Pcr。里查森外推公式为
(8)
式中n1为第一次的分段数,所得到的近似解为β1,n2为第二次的分段数,近似解为β2。使用里查森外推公式需要用到两次计算得到的近似解,这部分工作已经在前面做好了。
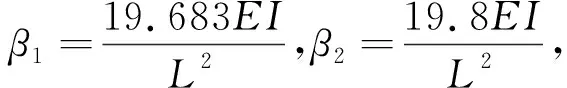
综合数据和图4可知:(1)误差由1.93%降低到0.540%,说明里查森外推法在减少计算工作量的同时能够快速减小误差。(2)两条曲线的斜率在n=10处均发生了突变,说明里查森外推法加快了求解的收敛速度。
5 结 论
(1)将差分法同遗传算法相结合应用于求解轴心受压杆件的临界荷载是一次全新的尝试,计算了n=2,…,10时的临界荷载值,使用里查森进行了一次外推,并将计算结果与精确解进行比较分析,分析的结果表明这种新的尝试得到的结果是可靠的。
(2)使用遗传算法在求解方程根的过程中需要对目标函数施加约束条件,且约束条件是随着方程的改变而变化的,这给求解过程带来了较大障碍。如何更好的解决这个问题,将是下一步研究的工作。
