基于PMSM的无传感器控制技术的研究①

2019-02-15李淑贤

佳木斯大学学报（自然科学版） 2019年1期

胡霞, 李淑贤

(安徽理工大学电气与信息工程学院，安徽淮南 232001)

0 引言

在矢量控制闭环速度调节系统中，若要落实PMSM的高性能追踪，则电机转子所处的地点和速度的回馈必须有更高的准确度。目前，最常用的监测方式是安装传感器，来及时发现转子所处的地点并算出电机的转动速度后回馈给整个操作的闭环回路里。但是这会有一系列的缺点，这将使电机的总体构造更加繁复，机械强度降低，因此需要采用软件的方法替代传统的传感器。为解决零速低速到高速的范畴内的无传感器问题，采用了复合控制的方法，可以更好的跟踪转子所处地点信息和转动速度，使其与实际值更加靠近，得到更好的操作性能。

1 永磁同步电动机的数学模型

了解PMSM的普遍方式是建造d、q轴数学模型。他不仅可以解释电机平稳特性，还可以解释电机的暂态特性。PMSM的d、q轴数学模型对转子所处地点的预测算法的解释与推演起着关键效果。处于转子参考坐标轴dr-qr的PMSM位于定子侧的电压方程为：

(1)

在公式(1)中，vdsr和vqsr、idsr和iqsr、ψdsr和ψqsr依次是处于转子侧参考坐标轴下的定子dr、qr轴电压、电流与磁链；rs是定子电阻；ωr是转子旋转角速度；p是微分算子。

电机定子磁链方程为：

(2)

图1 基于脉振高频注入法的PMSM无传感器控制框图

上式中，Ld、Lq依次为定子dr、qr轴电感；ψpm为转子永磁体产生的磁链。在dr-qr坐标轴中，qr轴磁链ψqsr通过qr轴电流iqsr进而产生的，dr轴磁链ψdsr通过dr轴电流idsr和永磁体磁链ψpm一起作用下存在的。当给定定子绕线电阻的更高频率的电压频率比电机转子的旋转角频率ωr更大时，dr轴与qr轴是彼此解耦的。因此，dr轴上改变的磁链没有使得qr轴上的电流产生变化。同时，思考到如果在qr通入给定的高频电压信号，可能会产生会生出大的转矩脉动。所以，从由更高频率电流引发的转矩脉动和生成的不必要的损耗方面来说，向dr轴上通入更高频率的电压信号能够得到最佳效用。

2 高频注入法原理

根据通入波形的种类可将高频注入法分类：旋转和脉振高频注入法。因为使用的永PMSM是表贴式的，选择了脉振注入来控制。

其工作机理是向预计的d′-q′坐标的d′轴流入高频率的正弦波电压激励，使φ-i特性曲线进入饱和区，直轴电感降低，电机产生磁饱和效应，出现了饱和凸极性的现象，然后利用电机磁饱和凸极性造成的两轴电感不一致，使q′电流中含有转子地点和转动速度消息。q′轴电流经过BPF后，再与一个和流入信号一致频率的高频电压信号相乘，之后使用LPF去掉高频信号，得到直流分量，即得到转子位置估计误差信号。利用某种控制方法使得误差为0，即可得到准确值。

操作方式使用的是传统的I*d=0转子定向闭环操作方式，使用PI来调控相应的调节器，选取合适的积分比例参数，可以使驱动系统整体都能够达到优异的动态和静态特性。

当使用脉振注入法来观察测量PMSM的转子所处位置和其速度时，如果dr、qr轴有不一致的高频率Z，即Zrdh≠Zrqh，Ldh≠Lqh，则半差高频率阻抗Zdiff≠0，在相应的高频率电流中存在有关于△θr的消息。因此，脉振注入法主要用于有着显著凸极效应的内置式PMSM。而对于表贴式PMSM而言，它由隐极型转子所构成，位于定子绕组上的直交轴电感Ld=Lq。所以，如果使用脉振注入法来检测有着不显眼特征的表贴式PMSM的转子所处位置和其速度，必须使得处于高频激励下的dr、qr轴的高频率电感不一致。然而，在面贴式PMSM的d轴永磁体的作用下，当流入定子绕组中的高频电流高到某种极限值时，高频阻抗展现了显眼的凸极性，即饱和凸极性。因此，脉振注入法不但能够用在拥有显著凸极性的内埋式PMSM，而且还可以用在拥有饱和凸极性的表贴式PMSM的转子所处位置和其速度检测上，只是必须要加大流入更高频率电压激励的频率和幅值。

图2 高频注入法仿真结果图

3 脉振高频注入法控制系统及仿真

图1中，I*d=0 为静止坐标系中三相至二相的坐标变换矩阵；I*d=0为二相由静止至旋转坐标系的坐标变换矩阵和逆矩阵；SVPWM为正弦波空间矢量脉宽调制器所用的是电压源激励的逆变器；LPF是一种被用作过滤的低通滤波器，其作用是去掉电流型闭环中存在的部分高频电流；PI调节器用于估计转子的位置与速度。因此采用传统的I*d=0操作方法。电流、转速控制设备由 PI操作，选择适当的积分和比例系数，以使整个传动部分具有优良的动静态特性。根据控制系统图，建立了在Matlab的Simulink平台上的系统模型。选中的 PMSM 的开关频率为 5kHz，高频电压的频率是1kHz，LPF通带边缘频率为150Hz，BPF低通带边缘频率为987Hz，高通带边缘频率为1.018kHz。为了所搭建仿真模型得出正确结果，参考转速设定为100r/min，仿真结果如图2：

从图2的仿真可以得出，当电机从零速上升到参考值100r/min时，转速估计误差在速度上升阶段有比较高的值，但是当速度开始继续上升并且能够稳定下来时转速估计误差会变得越来越小。由此可以说明，如果挑选的控制器参数和高频信号恰当，基于位置跟踪观测器的脉振高频注入的无传感器控制技术能够满足实际电机的操作要求。

图3 改进型滑模观测器估算转速以及转速误差变化曲线

图4 改进型滑模观测器估算转子位置与位置误差仿真波形

4 基于滑模观测器的无位置传感器控制

滑模变结构控制是VSC中的比较特殊的操作方式。这种控制策略与常规操作方法的最重要的不同之处在于这种控制存在不连续的特点，它能够使得系统的结构随着时间流逝发生变动。这种控制方式实现的关键在于滑模面函数的选择以及滑模增益的选取，既要保证收敛速度，也要使得由于滑模增益过大而引起的电机运行出现较大的震动问题难以产生。由于滑模控制对系统模型精度的要求不高，并且可以适应参数变化以及外部干扰，所以滑模控制是一种鲁棒性很强的控制方法。在三相 PMSM控制系统中，滑膜观测器是基于给定与反馈电流之间的误差原理产生的，并由所测得的误差来重新估算PMSM的反电动势，进而估算转子的速度。

图5 复合区转子位置估计值与实际值变化曲线

图6 复合区转子位置估计误差变化曲线

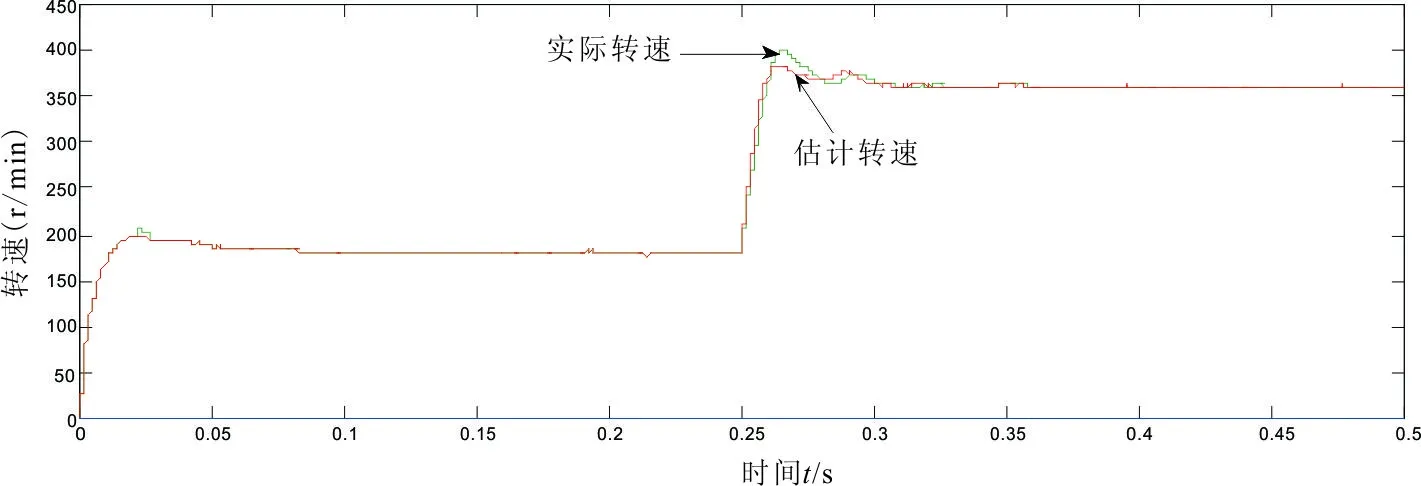
图7 复合区段的转速变化曲线

实际的控制系统，它会受到系统惯性的影响，再加上滑模观测器中的开关函数对系统带来的时间及空间上的滞后，将直接导致滑模变结构上出现抖振现象，造成反电势估算值中出现估算误差，而系统转子的速度和位置精度受到了抖振的影响，所以为了提高估算精度，必须要削弱抖振。传统的方法采用截止频率固定的低通滤波器，就会造成滑模电流观测器误差较大，用这种方法估算的转子转速和位置信息不准确。

针对上述问题，改善了滑模电流观测器，将开关函数用饱和函数进行替代，达到了降低高频抖振的效果；使用的LPF频率可随转速的改变而变化，即使转子位置得到了补偿，并且对转子位置和电机转速能达到更精确的估算，因此对滑模观测器的改进，有效的提高了系统的鲁棒性，并且改进型滑模控制拥有对系统参数不灵敏的特点。

为了更直观的反映理论的正确性，当电机速度突变时，研究系统的仿真情况，电机在启动前，维持住的轻载转矩，电机运行一段时间后，在0.08s改变电机的速度，速度由600rpm突变成1000rpm，对其转速、转矩、误差信息进行分析，仿真结果如图3、图4。

从图中可以看出，0.08s时转速由600rpm上升到1000rpm，在0时刻电机启动时以及0.08s转速突变时误差较大，随着转速的突变，转速误差在瞬间也有一定的波动，响应速度快，在很短时间内达到新的平衡。转子所处于的位置角波形周期随转速增加相应地变短，这表明预计的转子位置更准确。表明速度增加时，观测器对实际转子位置的预测更加准确，角度估计精度更准确。改进的滑模控制使用的是锁相环和优化后的反电势联合起来，对转子位置估算更加的优化，很好的控制了滑模中的抖振现象。

5 复合控制

前面分别对滑模观测器以及高频信号注入法的基本原理和性能作了详细的分析，当电机运行在中高速区段时，利用滑模观测器来预测PMSM的转子所处位置和其转动速度信息，这种操作策略在中高速域具有较高的精度，当电机运转的速度较低时，估算出反电势的峰值很小，信噪比很低，此时的滑模算法并不能精确的估算出反电动势值。就不能精确的转动速度以及位置消息。而高频注入法恰好相反，电机运行在零低速区域内，具有较好的估算精度，随着转速的升高，估算精度也变差，所以说在中高速阶段并不适用。若要实现在全速区域内无传感器控制，就要综合高频注入法以及滑模观测器算法在各自速度区间的优势，达到复合控制的效果，实现电机的全速域操作。把这两种方法进行加权复合，得出了电流与转速的双闭环操作方法。

永磁同步电机参数给定：电机启动转矩TL=2N·m，额定转速为n=1200rpm，注入频率fh=1000Hz。通过分析电机参数设定切换点上下限转速为额定转速的15%以及30%，即ωel=180，ωe2=360。在0.25s，速度由180rpm突变成360rpm，通过仿真结果观测到电机转子侧所处位置信息以及转速估计值与实际值之间的偏差，搭建复合操作的PMSM无传感器的仿真模型，并验证其成果。复合控制系统仿真波形如图5，图6，图7所示。