基于反常扩散模型的页岩气藏压裂水平井产能研究

李勇明，吴 磊，陈 希

（西南石油大学油气藏地质及开发工程国家重点实验室，四川成都610500）

随着我国油气资源形势的日益严峻，页岩气等非常规天然气资源的开发成为热点，而我国海相页岩气储层分布范围广、可采储量大，已成为我国天然气工业增储上产的关键[1-4]。但页岩储层具有低孔、基质渗透率低、致密等物性特征，生产过程中往往伴随着吸附解吸、扩散以及多尺度介质中的流动[5-6]，常规的产能模拟方法不能准确模拟页岩气藏生产时压力、流量的变化动态。国内外学者针对这个问题展开了大量研究，Al—Ahmadi等[7]建立了三重孔隙双裂缝模型，模拟天然裂缝性页岩气藏的瞬时压力、流量变化，但并没有研究扩散作用对产能的贡献；Ezulike等[8]建立了基质向天然裂缝和水力裂缝同时供气的多级压裂页岩气井产能模型，但忽略了气体的解吸和扩散的影响；Tian等[9]完善了Ezulike等建立的产能模型，考虑了基质中气体解吸和扩散作用，但只描述了天然微裂缝和水力裂缝间的扩散机理，没有考虑天然微裂缝在整个生产过程中的影响；Thorstenson等[10]研究了关于Fick 扩散定律描述多孔介质中的气体扩散行为；田冷等[11]考虑页岩气解吸、扩散等渗流机理，建立了页岩气藏多级压裂水平井产能模型。由于页岩储层超低孔、低渗特征，并且天然裂缝多发育，实际生产多采用水平井分段压裂及体积压裂技术，达到沟通天然微裂缝及增加缝网复杂度的目的[12-13]，这使得天然裂缝性页岩气藏表现出多种非均质性，使孔隙形状、结构表面、渗流路径具有分形的特征，渗流行为复杂反常，而分形结构复杂介质中的流体渗流不再符合经典的达西规律[14-17]，常规多孔介质流动模型不再适合天然裂缝性页岩气藏。因此，将分数阶导数反常扩散方程模型引入到页岩气压裂水平井三孔隙三线性流模型，推导出更加符合多级压裂页岩气藏渗流特征的复合模型，通过拉普拉斯变换求出模型的解，再通过Stehfest 数值反演得到了多级压裂页岩气水平井无因次产量，根据产量递减曲线特征划分了储层流动阶段，并研究了页岩气产能的影响因素。

1 反常扩散模型

相比于常规储层，页岩气藏在气体赋存状态、渗流孔隙及机理等方面具有较大差异，往往表现出多种非均质性，如具有人工裂缝、天然微裂缝、宏观孔隙、微纳米孔隙以及有机质体等，致使均匀介质假说在一般条件下是不成立的，而且由于孔隙尺度的突变和基质与裂缝性质的显著差异，使页岩气藏中速度场表现出急剧的不连续性和无规则性，这些非均匀的速度场不能用达西定律表征，因而采用反常扩散模型来表征[18]。

基于分形多孔介质中时间分数阶反常扩散方程模型，利用时间分数阶达西方程描述裂缝性页岩气藏中流体渗流[19-21]：

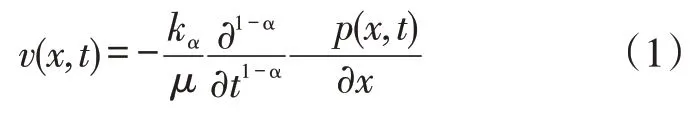
式中：α 为反常扩散指数，且0 ≤α ≤1。

当α=1时，式（1）变为经典的达西方程：

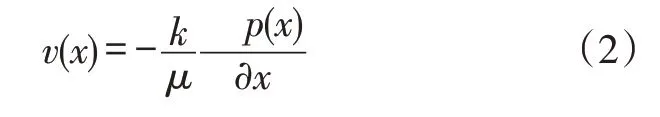
根据Caputo等人[22]的研究，时间分数阶导数的计算利用下式进行：

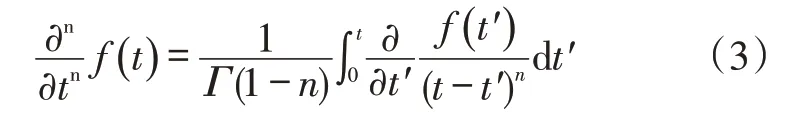
式中：n表示时间阶数。

2 页岩气藏压裂水平井产能模型

2.1 物理模型及假设条件

假设有一封闭矩形页岩气藏，气藏厚度为h，气藏宽度为2wF，气藏长度与水平井段长度相同且都为L，一水平井位于矩形气藏中心位置且定压生产。图1所示为多级压裂页岩气水平井物理模型，模型考虑了三种介质：人工裂缝、天然裂缝和基质，人工裂缝的间距为LF，天然裂缝的间距为Lf。为了便于求解，对模型做出如下的假设：①气体流动是三线性流，首先从基质流向天然裂缝，再由天然裂缝流向人工裂缝，最后由人工裂缝流向水平井筒直至被采出；②页岩基质中同时存在自由气与吸附气，气体的解吸用Langmuir 等温吸附方程描述；③气体流动过程中不考虑滑脱效应；④水平井压裂后水力裂缝方向与水平井筒垂直，且等间距、等长度分布。

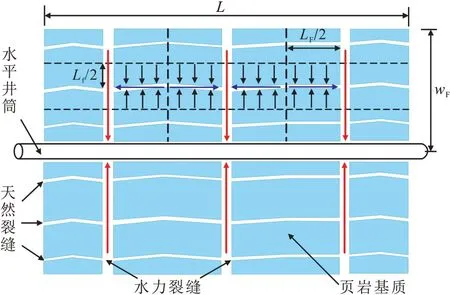
图1 页岩气藏压裂水平井物理模型Fig.1 Physical model of fractured horizontal well in shale gas reservoir

2.2 产能公式推导

为了方便推导和获得无因次产量，定义各无因次变量如下：

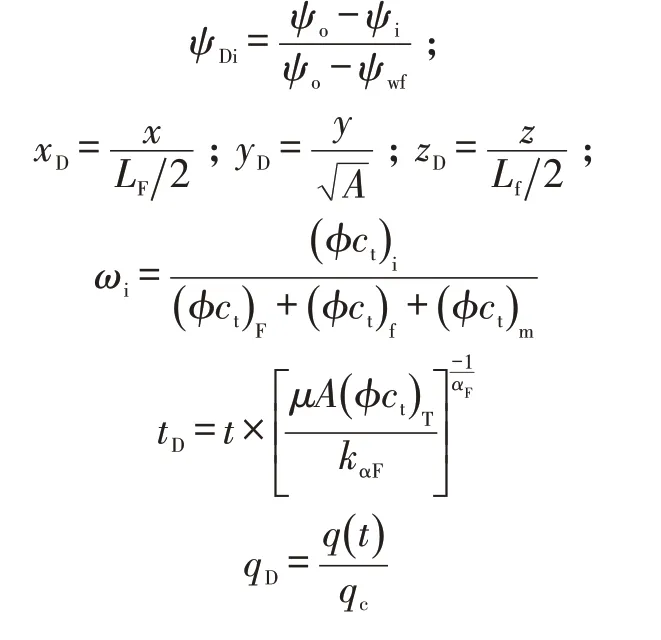
2.2.1 基质渗流数学模型

在基质区利用时间分数阶扩散方程表征页岩气的产出，气体解吸附采用Langmuir 等温吸附方程表征，并考虑页岩基质的压缩性，根据上述特征，建立页岩基质渗流微分方程如下所示：

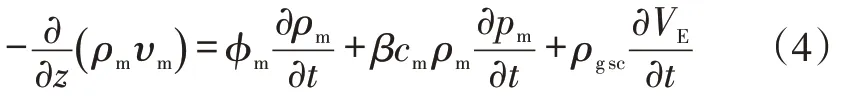
定义气体拟压力：

式（6）中：

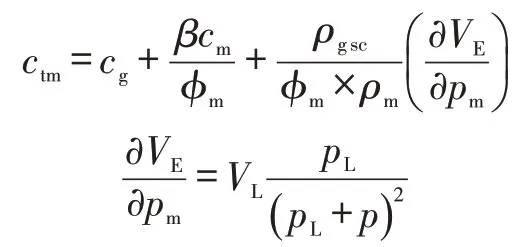
将基本微分方程、初始条件和边界条件无因次化，然后进行拉普拉斯变换得：

式（7）中：

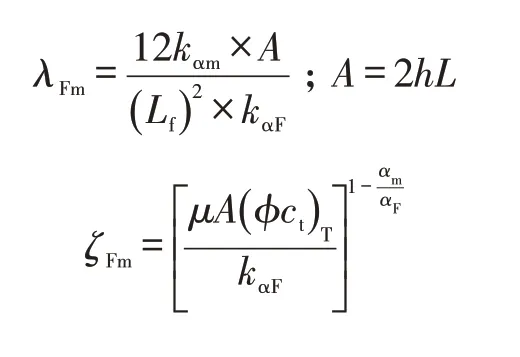
2.2.2 天然裂缝渗流数学模型

假设在相邻两条水力主裂缝中间存在着一个不渗透边界，天然裂缝中的气体渗流用时间分数阶达西方程表征，则建立天然裂缝中流动连续性方程为：

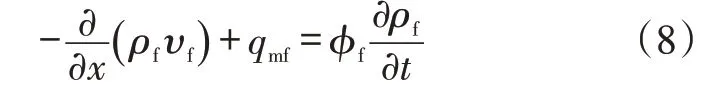
式中：qmf是页岩基质向天然裂缝系统的窜流量，且

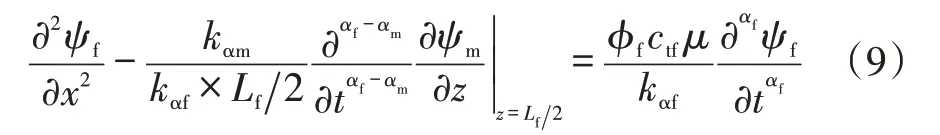
再将基本微分方程、初始条件和边界条件无因次化，然后进行拉普拉斯变换得：

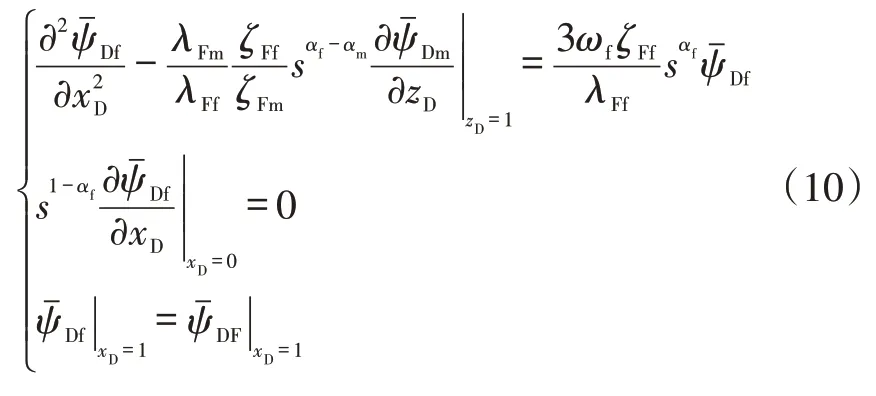
式中：

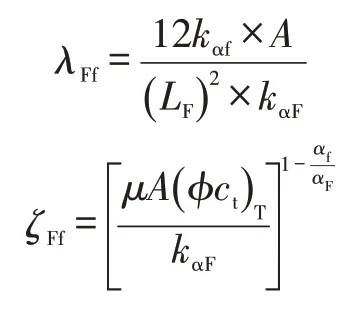
2.2.3 人工裂缝渗流模型

人工裂缝中气体渗流用时间分数阶渗流方程表征，建立连续性微分方程为：

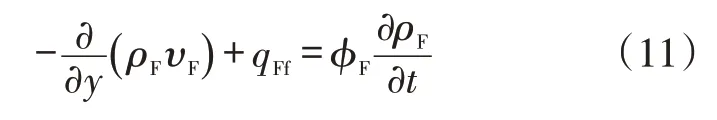
式中：qFf是天然裂缝向人工裂缝系统的窜流量，且

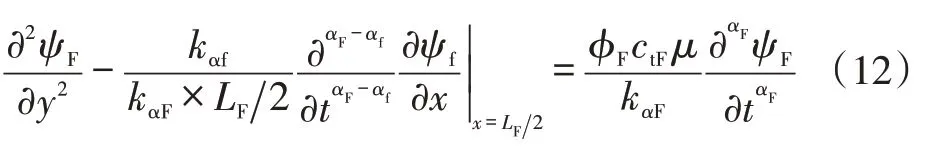
再将拟压力形式基本微分方程、初始条件和边界条件无因次化，然后进行拉普拉斯变换得：

2.3 产能模型求解

首先，由页岩基质的微分方程和边界、初始条件进行求解，可得页岩基质拟压力拉氏空间解：

然后，由天然裂缝的渗流微分方程和边界、初始条件，结合式（14），求出天然裂缝拟压力拉氏空间解：

式中：

最后再将天然裂缝的拟压力拉氏空间解代入到人工裂缝的渗流方程中，结合初始、边界条件，得到人工裂缝拟压力拉氏空间解为：

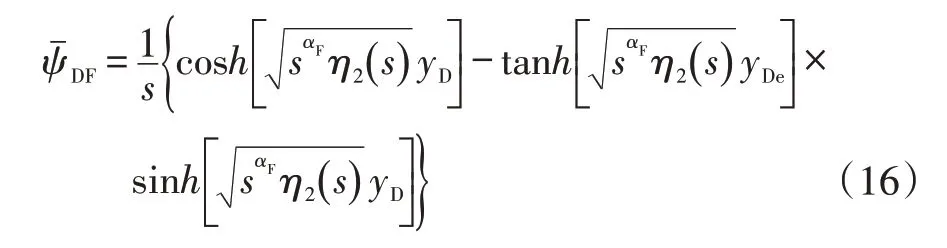
式中：

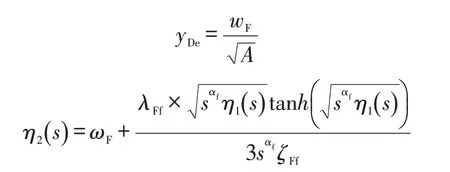
基于时间分数阶的达西方程，可得到井筒流量为：

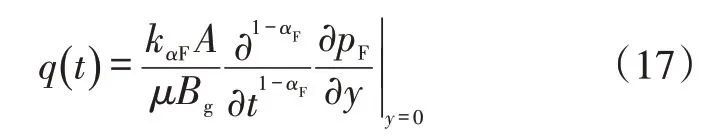
将上式进行无因次化得：

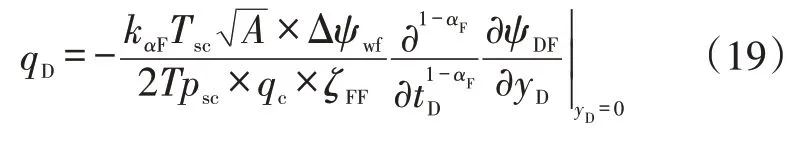
式中：

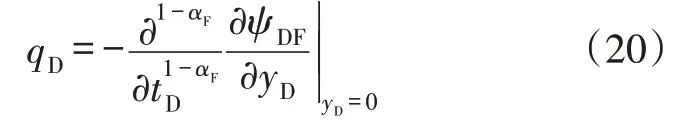
再将无因次化的井筒流量变换到拉普拉斯空间，并结合人工裂缝拟压力拉氏空间的解，得到井筒流量在拉普拉斯空间的解为：

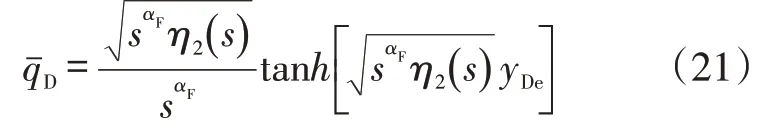
将拉氏空间的井筒流量转换为指数形式为：

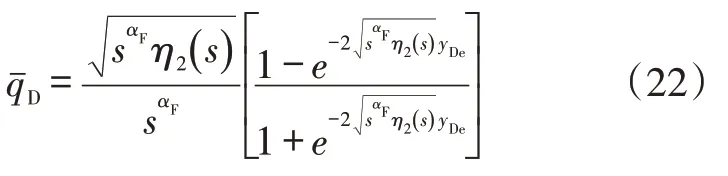
根据式（22）计算可以得到拉氏空间中的井筒无因次流量，然后再通过Stehfest 数值反演[23-24]，得到实时域空间的无因次产量。

3 实例计算与分析

某页岩气藏的基本参数如表1所示，应用建立的产能模型进行求解，得到无因次产量和无因次时间双对数特征曲线（图2）。

根据表1 参数计算并绘制出多级压裂页岩气藏的无因次产能特征曲线，如图2所示。

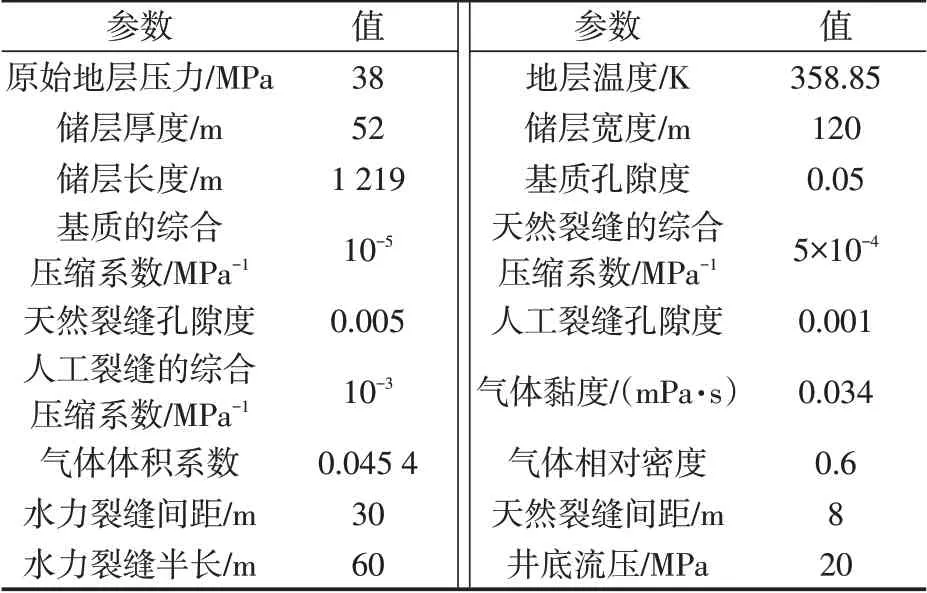
表1 某页岩气藏基本参数Table 1 Parameters of shale gas reservoir

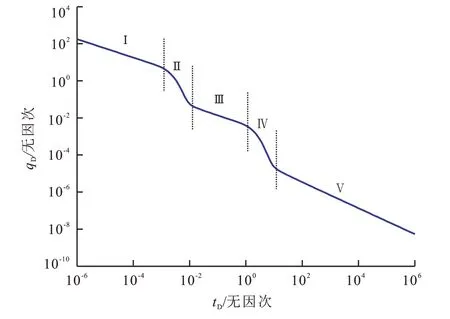
图2 页岩气藏压裂水平井无因次产能曲线及流动阶段划分Fig.2 Dimensionless gas productivity curve of fractured horizontal well in shale gas reservoir and different flow phases

从图2可得出，根据不同时段对产能占主导地位的储层渗流特征，页岩气藏压裂水平井无因次产能曲线可以划分为五个阶段：

Ⅰ：第一阶段主要为人工水力裂缝的线性流阶段，持续时间较长；

Ⅱ：第二阶段主要为人工裂缝和天然裂缝的双线性流阶段，天然裂缝开始向水力裂缝供气，出现天然裂缝向水力裂缝的窜流作用；

Ⅲ：第三阶段主要为天然裂缝的线性流阶段，持续时间较短；

Ⅳ：第四阶段为天然裂缝和基质的双线性流阶段，页岩基质开始向天然裂缝供气，出现基质向天然裂缝的窜流作用；

Ⅴ：第五阶段主要为页岩基质的线性流阶段，持续时间最长，对气藏生产后期的贡献很大。

3.1 反常扩散指数的影响

对页岩基质的反常扩散指数αm分别取0.3，0.6，1，得到如图3 所示的多级压裂页岩气藏无因次产能特征曲线。

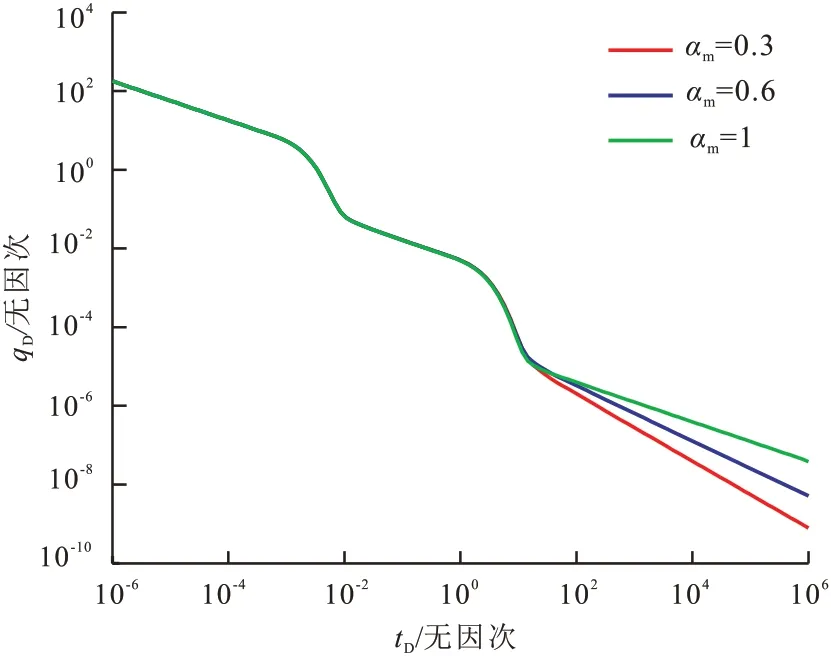
图3 页岩基质的扩散指数对产能的影响Fig.3 Effect of shale matrix diffusion exponent on the gas productivity

从图3 可得出：页岩基质的反常扩散指数αm对产能曲线有显著的影响，主要影响基质的线性流阶段，扩散指数越大，曲线的斜率越小，页岩气藏的产能降低幅度显著减小。这是由于αm=1 时，储层渗流为达西流动，当αm＜1 时，页岩基质非均质性越强，流体渗流不连续性和不规则性越强，流体流动越偏离达西流动，导致气藏产量递减显著。

3.2 拟渗透率的影响

当反常扩散指数值都为0.9时，分别取天然裂缝的拟渗透率kαf为0.01×10-3μm2·d0.1、0.1×10-3μm2·d0.1、1×10-3μm2·d0.1；人工裂缝的拟渗透率kαF为50×10-3μm2·d0.1、500×10-3μm2·d0.1、5 000×10-3μm2·d0.1，得到如图4、图5所示的页岩气藏无因次产能曲线。

从图4 可得出：天然裂缝的拟渗透率kαf主要影响天然裂缝线性流时期和基质与天然裂缝双线性流时期的产能，kαf越大，天然裂缝线性流持续时间显著减少，基质向天然裂缝供气阶段会提前发生，而且基质线性流持续时间增加；由此可见，天然裂缝对页岩产能有显著的贡献。

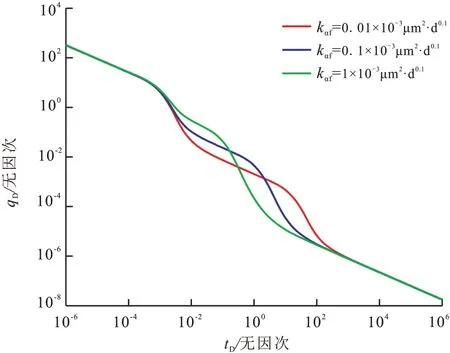
图4 天然裂缝的拟渗透率对产能的影响Fig.4 Effect of natural fracture pseudo-permeability on the gas productivity

从图5可得出：人工裂缝拟渗透率kαF主要影响产能曲线的中后期，其中对天然裂缝线性流期和基质线性流期影响较大，当kαF较小，在人工裂缝和天然裂缝双线性流时期，页岩气藏产能降低幅度减小，且天然裂缝线性流持续时间显著减少，基质向天然裂缝供气提前发生，而且后期页岩基质能够维持较长时间的线性流阶段。人工裂缝的拟渗透率对多级压裂页岩气藏的产能具有重要的作用。

3.3 储容比的影响

图5 人工裂缝的拟渗透率对产能的影响Fig.5 Effect of hydraulic fracture pseudo-permeability on the gas productivity

模型中考虑了人工水力裂缝、天然裂缝，为了能够直观分析两种介质的弹性储容比对产能的影响，分别对水力裂缝的弹性储容比ωF取0.01，0.03，0.07；天然裂缝的弹性储容比ωF取0.01，0.03，0.07，得到如图6a、图6b所示页岩气储层无因次产能特征曲线。

从图6a可以看出：水力裂缝弹性储容比ωF主要影响页岩气藏生产过程的早期，且储容比越大，页岩气藏的无因次产量越高，早期水力裂缝的线性流时间也越长，天然裂缝向水力裂缝窜流到来的时间也越晚；但水力裂缝的弹性储容比增大到一定程度时，页岩气藏产量增加幅度减小。

从图6b可以看出：天然裂缝的弹性储容比ωf主要影响页岩气藏生产过程的中期，即天然裂缝线性流期和页岩基质向天然裂缝的窜流期，当天然裂缝的弹性储容比ωf较大时，气藏的产量越高，天然裂缝线性流持续的时间也越长，基质向天然裂缝窜流发生的时间也越晚，这说明了页岩气藏压裂过程中应该形成复杂的裂缝系统，打开天然裂缝，增加天然裂缝的储容比，提高天然裂缝线性流时间，增加页岩气井的产量。

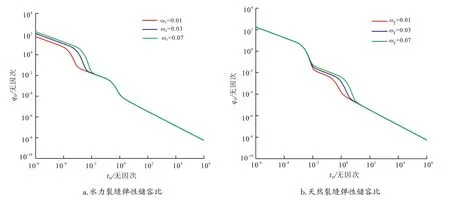
图6 储容比对产能的影响Fig.6 Effect of storability ratio on the gas productivity

3.4 窜流作用的影响

气藏在生产过程中会发生气体从天然裂缝向人工裂缝的窜流阶段，为了分析窜流作用对产能的影响，取天然裂缝向人工裂缝的窜流系数λFf为0.1，1，10；得到图7所示的页岩气无因次产能特征曲线。

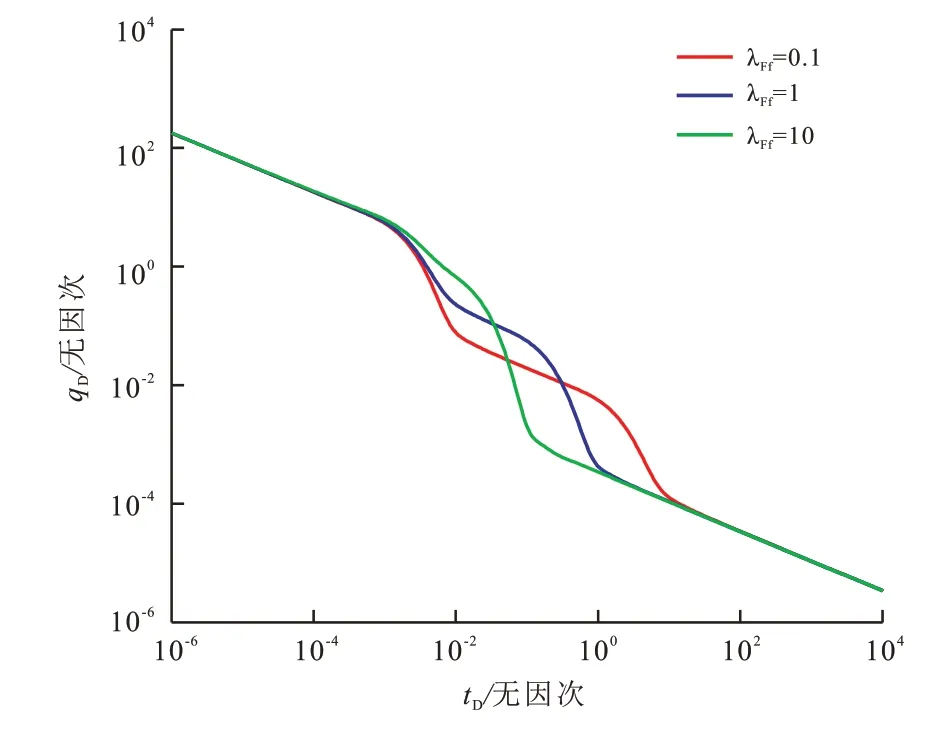
图7 天然裂缝—人工裂缝窜流对产能的影响Fig.7 Effect of fluid channeling between natural fracture and hydraulic fracture on the gas productivity

从图7可得出：天然裂缝向人工裂缝窜流作用的影响主要集中在人工裂缝和天然裂缝双线性流时期和天然裂缝线性流时期，当窜流系数较大时，无明显双线性流期，直接过渡到天然裂缝线性流时期，且天然裂缝线性流期持续时间显著减少，基质向天然裂缝窜流阶段会明显提前，这说明页岩储层中天然微裂缝通过沟通基质与水力裂缝对产能产生很大影响。

3.5 裂缝间距的影响

为了判断裂缝间距的大小对压裂井产量的影响，分别选取15 m，30 m，45 m 三种间距进行计算。计算结果如下图8所示。

从图8可以得出：水力裂缝间距主要影响生产的中期，在水平井筒长度一定时，裂缝间距越小，对应的裂缝条数越多，产能也越大；但随着压力的传播，裂缝间距越小，缝间发生压力干扰越早，产量递减也越早。所以进行增产改造时，应该优化裂缝间距，使储层最有效的开发。

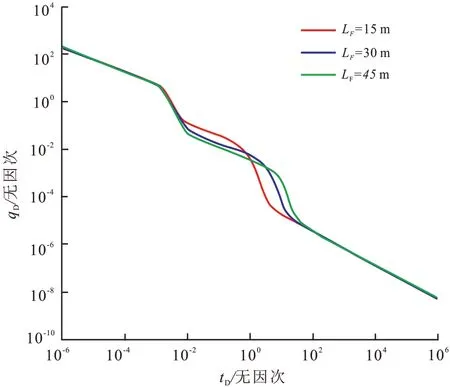
图8 裂缝间距对产能的影响Fig.8 Effect of fracture spacing on the gas productivity

4 结论

1）运用分形多孔介质的反常扩散模型，推导了考虑天然裂缝存在的页岩气藏压裂水平井产能模型，并利用拉氏变换和Stehfest 数值反演方法对产能模型进行了求解，绘制出页岩气藏压裂水平井产能特征曲线，并进行了实例计算与分析。

2）根据无因次产能特征曲线，划分页岩气藏压裂水平井的流动阶段，结果表明：考虑反常扩散模型时，储层有人工裂缝线性流、天然裂缝和人工裂缝双线性流、天然裂缝线性流、基质和天然裂缝双线性流、基质线性流五个流动阶段。

3）反常扩散指数越小，页岩基质非均质性越强，渗流越偏离达西流动，产量递减幅度越大；天然裂缝拟渗透率通过缩短天然裂缝线性流期持续时间，使基质向天然裂缝供气提前发生，对气藏产能产生较大影响；人工裂缝拟渗透率越大，天然裂缝线性流持续时间显著增加，基质向天然裂缝供气发生时间越晚。

4）人工裂缝、天然裂缝的弹性储容比分别影响产能曲线的早期、中期，且储容比越大，产能的增幅显著；窜流系数越大，天然裂缝线性流期持续的时间越短，基质向天然裂缝供气阶段越早出现；水力裂缝间距主要影响生产的中期，裂缝间距越小，水力裂缝间干扰越早出现，中期产量递减越快。

符号说明

υi为气体渗流速度，m/s；αi为反常扩散指数；kαi为拟渗透率，10-3μm2·s1-α；μ为页岩气黏度，mPa·s；s为拉氏变量，无因次；pi为储层压力，MPa；t 表示时间，s；Γ 为伽马函数；ρi为气体密度，kg/m3；ρgsc为标准状况下气体密度，kg/m3；ci为压缩系数，MPa-1；n 为时间阶数；β 为有效压缩系数，无因次；VE为气体解吸量，m3/kg；ϕi为孔隙度；ψi为气体拟压力，MPa/s；Z 为气体的压缩因子，无因次；M 为页岩气摩尔质量，kg/mol；R 为理想气体常数，8.314 J/（mol·K）；T为储层温度，K；pL为Langmuir压力，MPa；VL为Langmuir体积，m3/kg；ωi为弹性储容比；ϕT为储层总孔隙度；λ 为窜流系数；A为井筒泄流面积，m2；Lf为天然裂缝间距，m；cti为综合压缩系数，MPa-1；cg为气体压缩系数，MPa-1；为拉氏空间无因次拟压力；h为储层厚度，m；L为水平井筒长度，m；cT为储层总压缩系数，MPa-1；tD为无因次时间；qmf为基质向天然裂缝的窜流量，kg/（m3·s）；LF为水力裂缝间距，m；qFf为天然裂缝向水力裂缝的窜流量，kg/（m3·s）；y 为垂直于水平井筒方向的流动距离，m；wF为储层半宽度，m；xD,yD,zD为无因次距离；Bg为气体体积系数；psc为标准状况下气体压力，MPa；Tsc为标准状况下气体温度，K；q为井筒流量，m3/s；ψwf为井底拟压力，MPa/s；qD为无因次井筒流量；为拉氏空间的无因次井筒流量。

下角标：m代表页岩基质；f代表天然裂缝；F代表水力裂缝；o代表原始条件；D代表无因次属性。