压裂水平井水电模拟实验边界修正方法
2019-02-15李琳琳
李琳琳
(中国石化石油勘探开发研究院,北京100083)
水平井压裂造缝技术是一项十分有效的增产措施,特别在开发页岩气藏和致密气藏等方面具有无可比拟的优越性。裂缝的存在使得水平井周围渗流特征发生了显著变化,有效地扩大了渗流体积[1-4]。因此,有许多油藏工作者针对压裂水平井的生产渗流情况采用实验手段进行了研究。其中,水电模拟实验是研究裂缝特征参数以及裂缝位置对生产影响的有效方法[5-12]。但是该方法仍存在着较大的缺陷,当水电模拟实验的外边界被设定为定压边界时,在进行裂缝距离(或水平井筒长度)对单井产量影响的研究时,裂缝到边界距离变化对产量的影响往往很大,当裂缝距边界越近,它的产能提高的就越显著,从而所得出的裂缝间距与产量的关系,实际上是裂缝间距与裂缝到边界距离共同作用的产量变化关系。因此,提出了一种新的方法来消除边界的影响,实现真实的裂缝间距与产量的变化关系,为水平井压裂设计提供有效指导。
1 水电模拟原理
水电相似原理指控制均质流体通过多孔介质流动的微分方程与控制电荷通过导体材料流动的微分方程之间具有相似性。即用导电介质模拟地层,在介质上施加一定电势差产生的电场来模拟地层中的稳定渗流场。
多孔介质中流体的流动遵守达西定律:
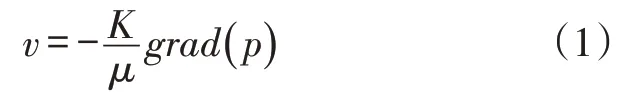
式中:v 为流动速度,cm/s;K 为渗透率,μm2;μ 为黏度,mPa·s;p为压力,10-1MPa。
通过导体的电流遵守欧姆定律:

式中:I为电流,A;ρ为电导率,S;U为电压,V。
不可压缩流体通过刚性多孔介质稳定流动的连续性方程:
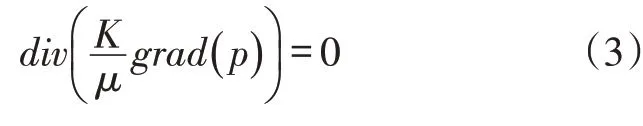
导体中稳定电流,其电压满足方程:
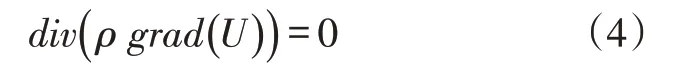
对比式(1)~式(4),可以看出,在电压作用下电流的流动规律与油层压差作用下油层流体的渗流规律完全相同,二者之间存在相似关系。因此,在满足几何相似、性质相似、物理相似、时间相似以及初始边界条件相似等五个相似条件后,不可压缩流体的稳定渗流问题可用稳定电流的流动进行模拟。
2 油藏模型与实验装置
2.1 油藏模型
假设存在某均质油藏,上、下边界封闭,供给外边界为圆形定压边界。在油藏中存在一口压裂水平井位于油层中心,水平井筒不生产,有三条与水平井筒方向垂直的裂缝,地层流体由裂缝流入井筒,裂缝在垂向上贯穿油藏。压裂水平井生产压差为2 MPa;圆形定压边界半径500 m 或1 500 m;油层渗透率为3.0×10-3μm2;地层原油黏度为1.415 mPa·s。
2.2 相似准则
要使油藏模型与实验模型相似,必须满足几何相似、压力相似、阻力相似、运动相似以及流量相似五个条件。在水电模拟实验中,渗流场和电流场对应关系如表1 所示,二者在几何上满足相似条件,其中电极电位对应于井或边界的压力,电解液的电阻对应于地层流体的渗流阻力,电流对应于地层中流体的流量,电解液的电导率对应于地层中流体的流动系数。模型满足相似准则以后,根据所测电流值就可计算出井的产量,这样就可以把水电模拟实验和实际油藏模型联系起来。

表1 渗流场和电流场的模拟关系对应Table 1 Correspondence of seepage field and current field
2.3 水电模拟实验装置
水电模拟实验装置由油藏模拟系统、低压电路系统和测量系统三部分组成(图1)。以适当浓度的CuSO4溶液模拟储层,以紫铜带模拟供给边界,以紫铜片模拟裂缝,以康铜丝模拟井筒。铜丝与电解液不接触的地方用胶皮密封来模拟封闭水平段(水平井筒不生产,仅靠裂缝导流)。低压电路系统将220 V的交流电降到对人体安全的电压以下(36 V),供给边界接高电位[11]。
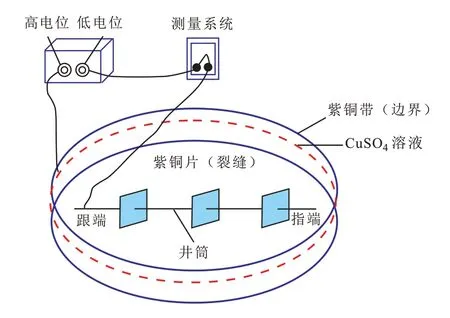
图1 水电模拟实验装置示意图Fig.1 Experimental device of water and electricity
3 实验流程及结果分析
3.1 多条裂缝位置与产能关系
假设地层中存在多条相互平行的垂直裂缝,如图2模拟了圆形定压油藏中三条裂缝生产的情形,通过改变裂缝的间距,分析裂缝间距对产能的影响。这种方法所得出的裂缝间距与产量的关系实际上是受到裂缝间距与裂缝到边界距离共同作用的结果,模拟结果如图3所示,压裂水平井产量(三条裂缝的总产量)随裂缝间距的增大而增大,且增大的幅度越来越大。此即为常规水电模拟实验方法中通常得出的结论。

图2 裂缝间距与产能关系实验(以三个位置为例)Fig.2 Fracture spacing and productivity(take three position as examples)

图3 裂缝间距与总产能关系曲线Fig.3 Relation between fracture spacing and productivity
3.2 消除边界影响的流程
为了消除边界影响,设计了一种新的方法,具体流程如下:
1)以三条缝为例,当三条缝分别置于图2a 时,分别测量每条单缝单独存在时的产量,记为m1i(i=1,2,3);然后将三条缝同时放入,测量每条缝的产量记为n1i(i=1,2,3),该值为存在缝干扰后的单缝产量;将这两组值作差,即求出图2a的缝间干扰值。
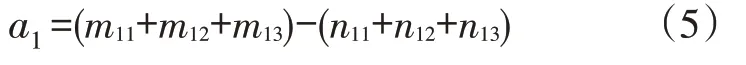
2)在图2b时,分别测量每条单缝单独存在时的产量,记为m2i(i=1,2,3);然后将三条缝同时放入,测量每条缝的产量记为n2i(i =1,2,3),同样求出图2b的缝间干扰值a2。
3)由图2a变化到图2b时,缝间干扰变强,其变化值为a1~a2,其中a1>a2。
4)求出由图2a变化到图2b造成的产量变化值b,该值是由缝间干扰变强以及裂缝到边界距离变大同时作用的结果:

因此,可将缝间干扰的因素从b 中剥离出来,即b-(a1-a2)。
5)由图2a变化到图2b时,记Q1=n11+n12+n13为图2a 的总产量,即可得到图2b的不受边界距离变化影响的总产量为:
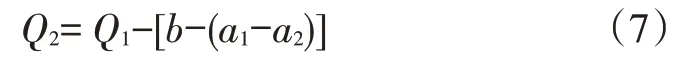
6)按相同的方法,在图2b 基础上,可求出图2c的产量,由此类推,即可得到不同位置处,单纯的裂缝间距与产量的关系曲线。
3.3 实验结论的验证
图4 为地层半径为500 m,存在与去除边界影响时水平井产量的对比。可以看出,消除边界影响后,在相同裂缝间距下总产量要比存在边界影响的产量小,且裂缝间距越大,两组数值差异越大。

图4 消除边界影响前后裂缝间距与总产能关系曲线Fig.4 Relation between fracture spacing and productivity before and after eliminating the boundary effects
为了验证以上方法的正确性,做了如下分析:假设圆形地层的半径为1 500 m,仍采用三条裂缝模拟。由于这时地层边界距离裂缝较远,边界对裂缝产量的影响可忽略不计,由此得出的水平井产量可近似为没有边界干扰,只存在缝间干扰作用(如图5中蓝色曲线)。将地层半径为1 500 m的水平井产量与去除边界影响后(地层半径为500 m)的水平井产能进行对比发现,两条曲线基本平行。由于边界大小不同,所提供的地层能量不同,因此产量大小存在差异,但是由于去除了边界的影响,在只受缝间干扰影响的情况下,两条曲线基本平行,这进一步验证了所提方法的正确性。
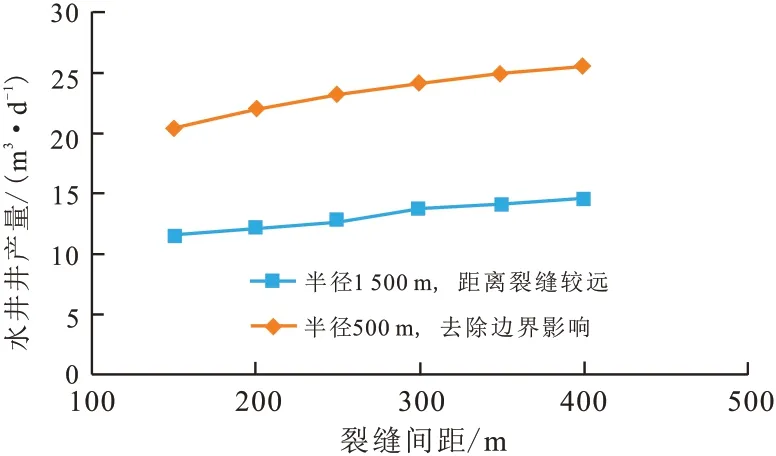
图5 裂缝间距与裂缝产能关系曲线Fig.5 Relation between fracture spacing and crack productivity
4 结论
1)常规的水电模拟裂缝间距对产能影响的结论:压裂水平井产量随裂缝间距的增大而增大,且增大的幅度越来越大,该结论很大程度上受到裂缝到边界距离变化的影响,因而与实际具有较大的差异。
2)通过消除裂缝到边界距离的影响,可以得到裂缝距离变化对水平井产能的影响;通过模拟供给面积很大的油藏,与去除边界影响的水平井产能与裂缝距离曲线对比,两曲线基本平行,证明方法正确可行。
