应力敏感性差异对天然裂缝储层直井产能的影响

曹 军，唐 海，吕栋梁，吴锦伟

（1.西南石油大学石油与天然气工程学院，四川 成都 610500；2.中国石化华北油气分公司勘探开发研究院，河南郑州062550）

低渗透油藏在投入开发以后随着流体产出，地层压力下降，使得储集层岩石发生变形，孔隙、喉道更加细小，导致渗透率和孔隙度变差的特征成为岩石的应力敏感性特征[1-7]。近年来，大量的学者对低渗透油藏应力敏感性进行了大量研究，研究中大多运用应力敏感系数表征岩石应力敏感强弱[8]。对低渗储层是否存在应力敏感存在较大分歧：一种认为低渗致密储层存在强应力敏感，另一种认为其存在弱应力敏感。齐亚东[9]等人在特低渗透砂岩储层应力敏感性实验中发现储层中微裂缝的闭合对产能影响很大。焦春燕[10]等人在超低渗透油藏应力敏感性实验研究中发现，岩心应力敏感分为两个阶段：微裂缝闭合阶段和基质受压阶段，应将其分别考虑。

目前低渗透油藏产能研究[11-13]大多局限于传统的经典渗流理论，通常忽略了基质与裂缝应力敏感差异的影响。天然裂缝是低渗透油田开发需要考虑的重要因素。实际储层中的天然裂缝发育极为复杂，必须对裂缝系统进行简化。有人建立了基于等效裂缝渗流模型的天然裂缝产能预测模型[14]，但未考虑应力敏感、启动压力梯度对渗透率影响；有人建立了考虑应力敏感和启动压力梯度的低渗透油藏直井产能公式[15]，但忽略了基质与裂缝应力敏感差异[16]对产能的影响。笔者基于前人研究，建立一种考虑基质与裂缝应力敏感性差异的天然裂缝产能预测模型求解方程。以长庆低渗油田基础数据为例，研究裂缝参数、基质应力敏感、裂缝应力敏感对产能的影响。

1 天然裂缝产能预测模型

1.1 模型假设

假定一个水平均质各向同性圆形等厚无限大地层中心存在一口完善井（图1、图2）。模型内圈为天然裂缝发育区，渗流分为裂缝内的线性流和基质的径向流，外圈为基质区域，渗流为平面径向流。

天然裂缝发育区域裂缝均匀分布，方向一致，均为垂直裂缝，裂缝在裂缝集中区储层平面上和纵向上完全贯通。相关假设条件：①天然裂缝内流动满足裂缝平板流模型，方向平行于流动方向；②流体为单相均质牛顿流体稳定流，符合达西渗流规律；③天然裂缝发育区域不考虑裂缝与基质间的微观渗流；④不考虑地层与裂缝的污染，忽略重力、毛管力的影响；⑤分别考虑基质、裂缝的应力敏感对渗透率的影响；⑥考虑启动压力梯度。

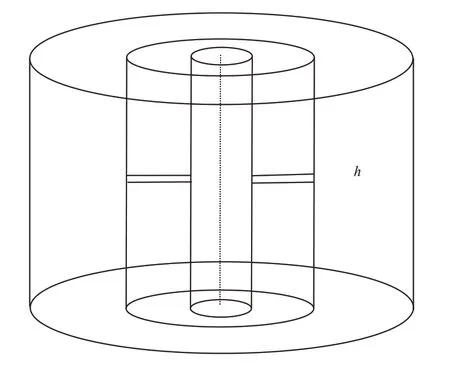
图1 天然裂缝产能预测模型示意图Fig.1 Prediction model of natural fracture productivity

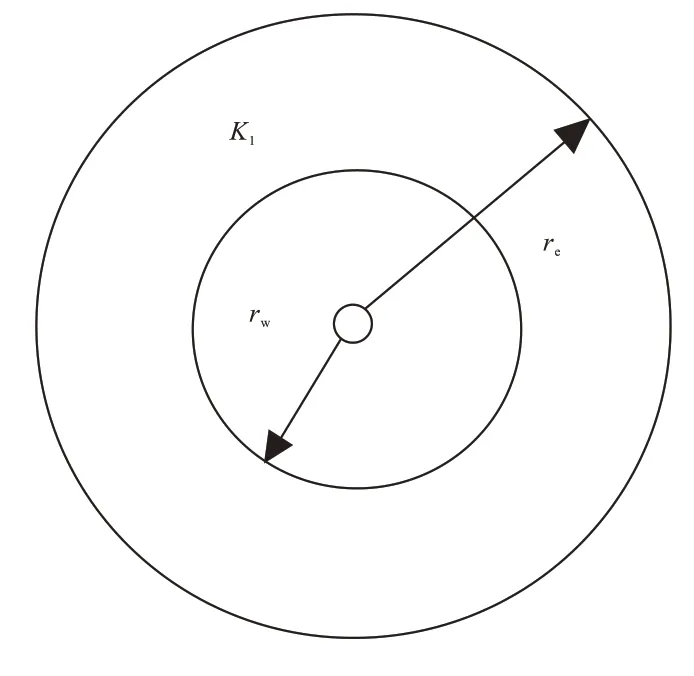
图2 模型的平面示意图Fig.2 Model plan

模型中需要的参数：油藏厚度为h，m；基岩渗透率 为K1，10-3μm2；天 然 裂 缝 初 始 渗 透 率 为Kf0，10-3μm2；天然裂缝渗透率为Kf，10-3μm2；油藏供给压力为pe，MPa；井底流压为pwf，MPa；内外区域交界处压力为p1，MPa；供给液半径为re，m；生产井半径为rw，m；裂缝发育集中区半径r2，m。裂缝宽度为Wf，m；裂缝条数为n 条；无裂缝区的流量q1，m3/d；裂缝集中区的流量q2，m3/d；基质区域的应力敏感指数α1，MPa-1；裂缝的应力敏感指数α2，MPa-1；启动压力梯度G ，MPa/m；原油体积系数Bo。

1.2 方程的推导

目前，大多数有关应力敏感性研究都是基于岩心渗透率与压差之间的关系研究[16]：

式中：K 为岩心渗透率，10-3μm2；Ki为原始渗透率，10-3μm2；a 为应力敏感系数，MPa-1；p 为地层压力，MPa-1；pe为re处的原始地层压力，MPa。

通过裂缝岩心与基质岩心的应力敏感性实验测试，分别拟合出裂缝应力敏感系数、基质应力敏感系数，为模型计算做好参数准备。

董利飞[17]等人在对不同渗透率岩心应力敏感性研究中发现，裂缝的存在会加强储层的应力敏感性，得出基质应力敏感性弱于含裂缝岩心，弱于人工裂缝岩心（即天然裂缝应力敏感系数a2大于基质应力敏感系数a1）。

整个渗流过程分为两个阶段：外圈的基质渗流和天然裂缝发育区裂缝和基质的流动。

外圈基质区域渗流，在（r2，re）的区间内为平面径向流，考虑启动压力梯度，基质岩心的应力敏感存在，对应的渗流微分方程为：

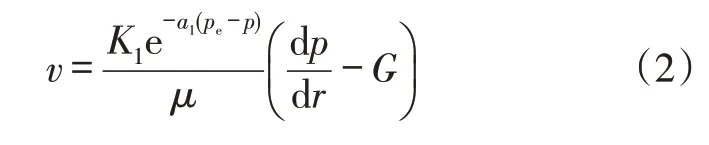
假设基于单相牛顿流体稳定流前提下，上式进一步化简：

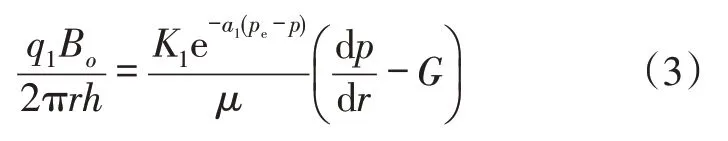
上式在（r2，re），（p1，pe）内积分，得：

天然裂缝发育区内的渗流等效为裂缝内的线性流和基质内的径向流动，流量分别qf和qr。

裂缝内的线性流动，考虑裂缝的应力敏感的存在：

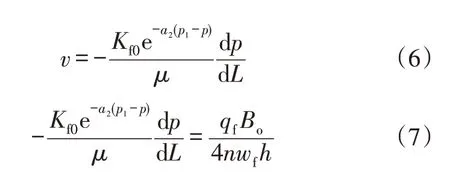
考虑裂缝宽度随渗透率的变化，参考油层物理[18]：

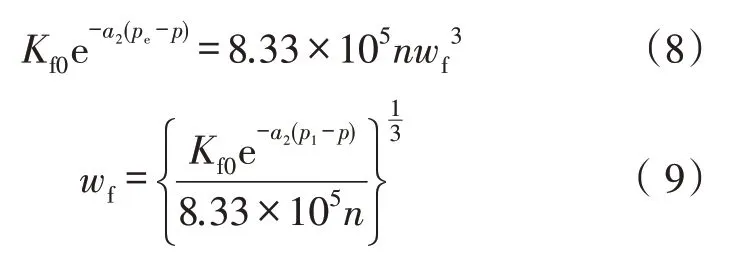
将式（9）参数代入式（7）在（rW，r2），（pwf，p1）内积分可得出裂缝内线性流流量qf：

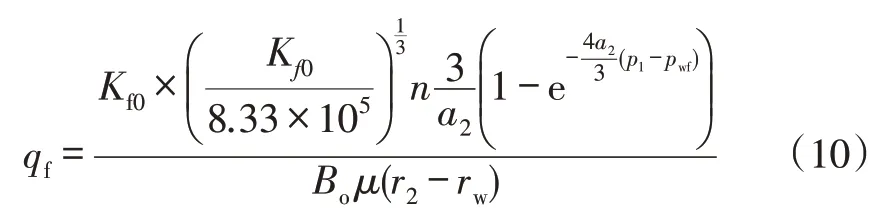
基质内的平面径向流，考虑基质应力敏感的存在，得：

则天然裂缝发育区的流量q2为：

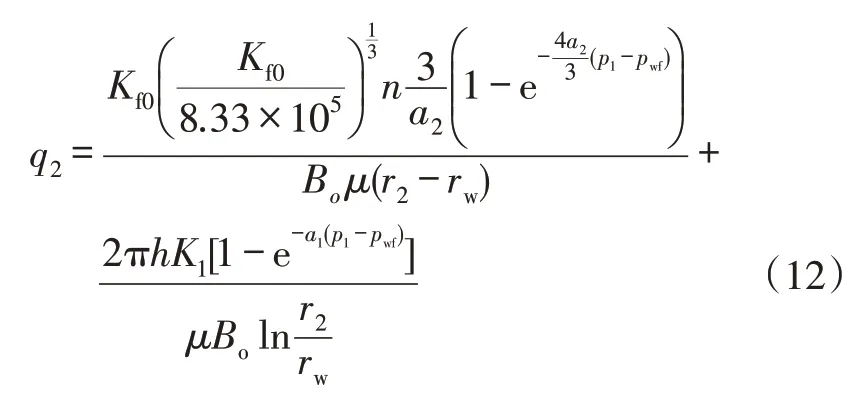
根据稳定流连续性关系，交界面处压力相等，流量相等，即q=q1=q2。利用二分法[19-20]的原理，给定不同的p1值（裂缝集中区与基质区交界处压力），使得q1、q2大致相等（达到相应的精度eps）。计算流程图见图3。

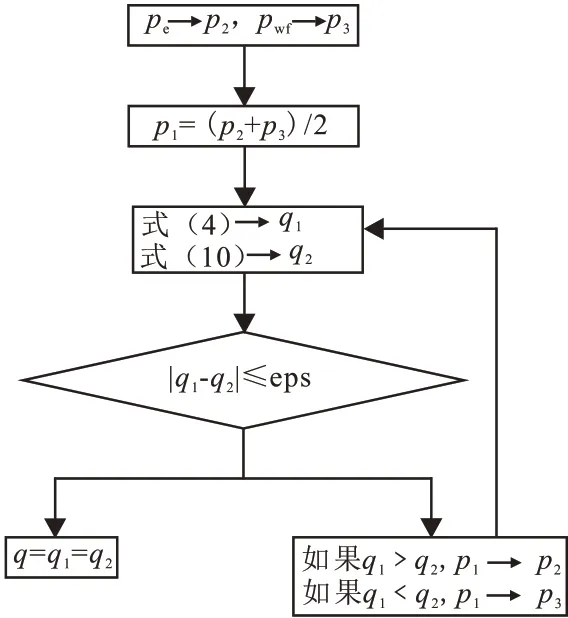
图3 模型计算流程图Fig.3 Calculation flow of model

结合（4）、（5）、（12）得出考虑应力敏感、启动压力梯度的天然裂缝储层产能方程。该方程考虑到启动压力梯度对产能的影响，以及裂缝岩心与基质岩心应力敏感性的差异对产能的影响，较前人的模型更加全面，因此，能更加准确地对天然裂缝发育低渗储层的产能进行评价。

2 实例分析

以长庆油田X 区块低渗透油藏为例，研究应力敏感差异、裂缝参数对天然裂缝储层产能的影响。计算所需基础参数与地质参数：裂缝渗透率1 000×10-3μm2，油层渗透率2×10-3μm2，裂缝长度3 m，裂缝条数3条，供给边界距离600 m，井半径0.1 m，油层厚度20 m，供给压力36 MPa，井底流压14 MPa，原油黏度为0.529 mPa·s，裂缝的 应力敏感系数为0.1 MPa-1，基质的应力敏感系数为0.01 MPa-1，启动压力梯度0.01 MPa/m，原油体积系数1.029 5。

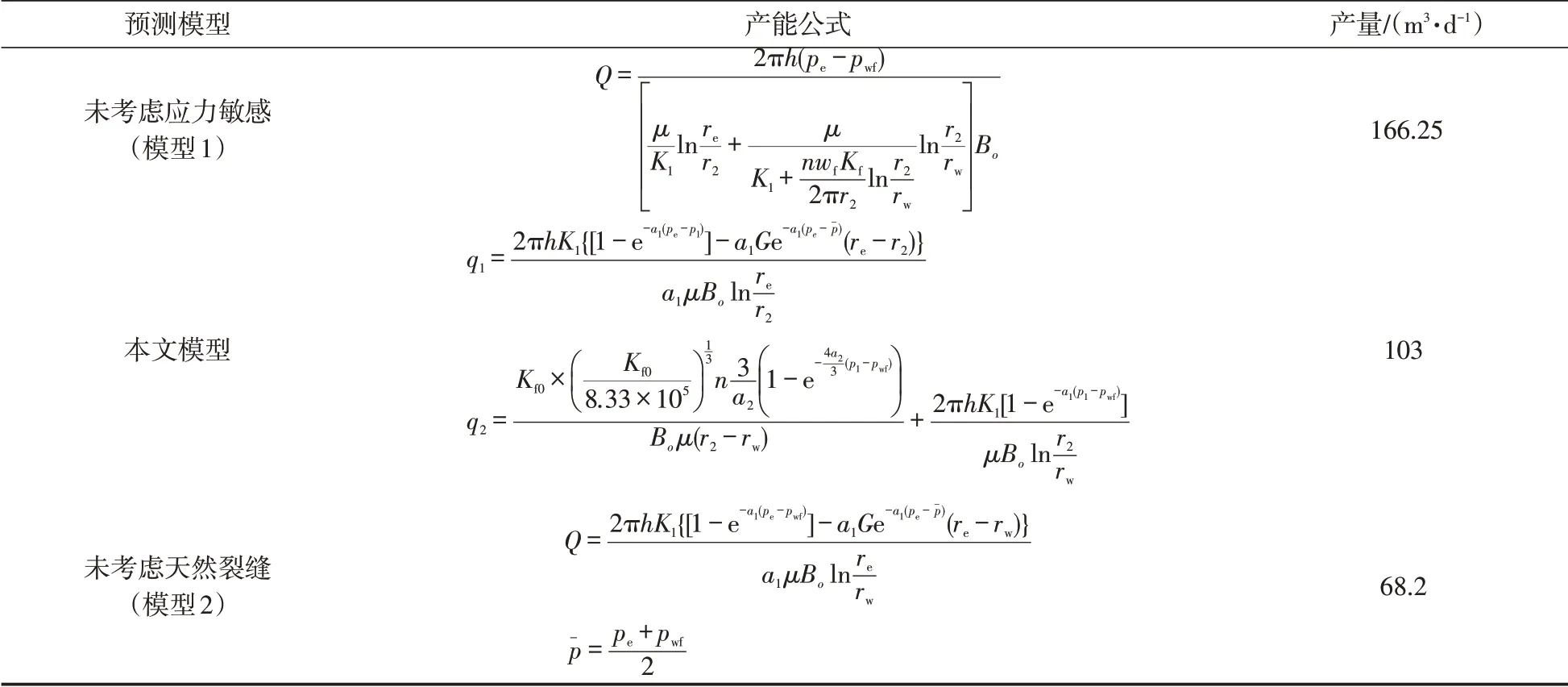
表1 不同模型的产能对比Table 1 Comparison of different models of production capacity

从计算结果表1可以看出，模型1计算出的产能偏高，产量比模型2 高出58 %，比本文模型高出38%，更加证实了应力敏感对低渗油藏产能的影响不容忽视。本文模型产量比模型2 高出33.8 %，可见，垂直于井筒的裂缝的存在对增产效果明显。

针对天然裂缝发育的低渗透油藏，以下从裂缝长度、初始裂缝渗透率、基质应力敏感系数、裂缝应力敏系数四个方面计算分析对产能的影响。

2.1 裂缝长度对产能的影响

保持其他数据不变，改变裂缝长度，取裂缝长度为0.5 m，1 m，1.5 m，2 m，3 m，5 m，10 m，15 m，用本文模型、模型1 分别计算每一个点产油量，得到裂缝长度与产油量的关系见图4。由图4可知，当裂缝长度每增加5 m，产油量后者比前者依次增加38.3%，8.3%，2.5%，可见裂缝长度小于5 m时，产油量增速明显；裂缝长度大于5 m 时，产油量增速放缓。未考虑应力敏感模型比考虑应力敏感模型产油量增速快，说明了天然裂缝发育储层不能忽视应力敏感性的存在。

图4 裂缝长度与产油量关系Fig.4 Relation between crack length and oil production

2.2 初始裂缝渗透率对产能的影响

本文裂缝渗透率基于裂缝平板流理论模型，初始裂缝渗透率越大，初始裂缝宽度越大。取初始裂缝渗透率0，250×10-3μm2，500×10-3μm2，750×10-3μm2，1 000×10-3μm2，2 000×10-3μm2，3 000×10-3μm2，4 000×10-3μm2，利用本文模型、模型1得出不同模型下产油量与初始裂缝渗透率之间的关系见图5。由图5 可知，当初始裂缝渗透率小于250×10-3μm2时（裂缝宽度较小），随着初始渗透率的增加，产油量增加明显，且本文模型的产量增速大于模型1；当初始裂缝渗透率大于250×10-3μm2时，产油量变化不大。这说明，井底裂缝初始渗透率（即裂缝宽度）达到一定值时，渗透率的增加对产油量影响不大；虽然裂缝宽度受到应力敏感的影响，但在裂缝宽度在一定范围内，裂缝宽度越大，对油井增产有利。

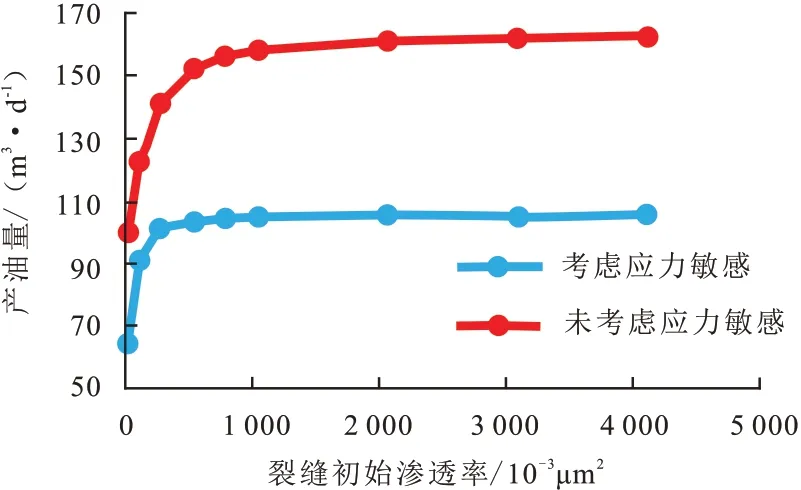
图5 初始裂缝渗透率与产油量关系Fig.5 Relation between initial fracture permeability and oil production

2.3 基质应力敏感系数对产能的影响

在裂缝长度分别为3 m，5 m，10 m，15 m 的情况下，保持基础数据不变，改变基质应力敏感系数α1，分别取0.01 MPa-1，0.03 MPa-1，0.05 MPa-1，0.07 MPa-1，0.09 MPa-1，利用本模型、模型2计算每一个点对应的产油量，得到两种模型基质应力敏感系数与产油量之间的关系见图6。由图6可知，随着基质应力敏感系数的增加，产油量逐渐降低。这说明，基质应力敏感越强，对低渗油藏的增产有不利影响。基质内天然微裂缝发育，基质的应力敏感性越强[21]。天然裂缝作为低渗油藏重要的渗流通道，其闭合对油井产量有重要的影响。

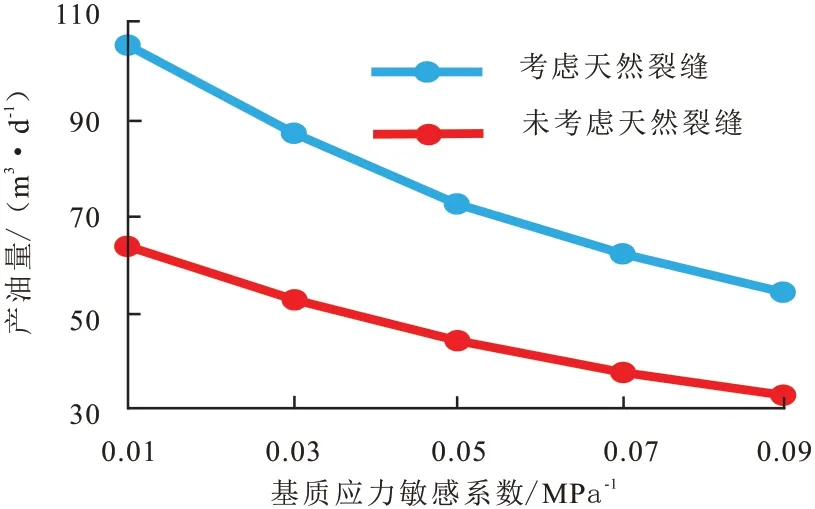
图6 基质应力敏感系数与产油量关系Fig.6 Relation between matrix stress sensitivity coefficient and oil production

2.4 裂缝应力敏感系数对产能的影响

初始裂缝渗透率分别为200×10-3μm2，300×10-3μm2，400×10-3μm2，500×10-3μm2的情况下，其他基础数据不变。改变裂缝的应力敏感系数，分别为0.1 MPa-1，0.15 MPa-1，0.2 MPa-1，0.25 MPa-1，0.3 MPa-1，利用本模型计算每一个点的产油量，得到不同初始裂缝渗透率下，裂缝应力敏感系数与产油量的关系见图7。由图7 可知，随着初始裂缝渗透率的增加，裂缝应力敏感系数对产油量的影响逐渐减弱。当裂缝初始渗透率较小时，随着应力敏感系数的增加，产油量下降明显，产油量依次下降12.9%、4.2%、1.7%、1%。由此说明，当裂缝宽度较小时，裂缝应力敏感系数对产油量的影响显著；当其超过该范围后，裂缝应力敏感系数对产油量的影响可以忽略，可见微裂缝对产能影响很大。

图7 不同初始裂缝渗透率下裂缝应力敏感系数与产油量关系Fig.7 Relation between fracture stress sensitivity coefficient and oil production under different initial fracture permeability

综上所述，裂缝初始渗透率在较低时，裂缝应力敏感强对产油量影响较大；当裂缝渗透率达到某一值时，初始造缝裂缝宽度对产量影响不大。裂缝长度对产油量增加明显，天然裂缝发育储层不能忽视应力敏感的影响。当对井底附近储层进行改造时，在裂缝宽度达到某一值后，再通过提高裂缝长度增加产油量。

3 结论

1）在前人的基础上，综合考虑基质、裂缝的应力敏感系数和启动压力梯度，建立了天然裂缝储层的产能预测方程。

2）分析了影响天然裂缝发育的低渗透油藏产能的主要因素，通过对裂缝参数、基质应力敏感系数、裂缝应力敏感系数的单因素、多因素关系的对比可知，基质应力敏感性越强，产能越低；裂缝宽度越小，裂缝应力敏感性对产能影响越大。

3）在对天然裂缝进行储层改造时，在裂缝渗透率和宽度达到一定值时，增加裂缝长度来提高产能。