共点力的平衡问题一二三
2019-02-15许文
许 文
(湖北省武汉市华中科技大学附属中学 430074)
物体在共点力作用下的平衡问题,是历年高考中重点考查内容之一,在近几年的全国卷与各地方卷中都有所体现,且考查非常灵活.高考命题热点有:(1)受力分析与共点力平衡问题;(2)动态平衡问题;(3)平衡中的临界与极值问题.本文通过解析一个条件、分析两种方法、讨论三类问题,帮助同学们有效地复习力的平衡考点内容.
一、一个条件
平衡状态是指物体处于静止或做匀速直线运动状态.平衡条件是物体受到的合力为零,即:F合= 0 .此条件应理解为沿任何一个方向上的合力均为零.若建立一个直角坐标系,则沿x、y方向的合力均为零,即:Fx=0,Fy=0.
二、两种方法
分析力的平衡问题有两种方法:(1)解析法:一般把力进行正交分解,分别在x、y方向上列出力的平衡方程,从而进行求解与分析;(2)图解法:当几个力的合力为零时,依次平移这几个力的矢量,可以组成一个首尾相接的封闭多边形,再通过此矢量图形进行分析与求解.
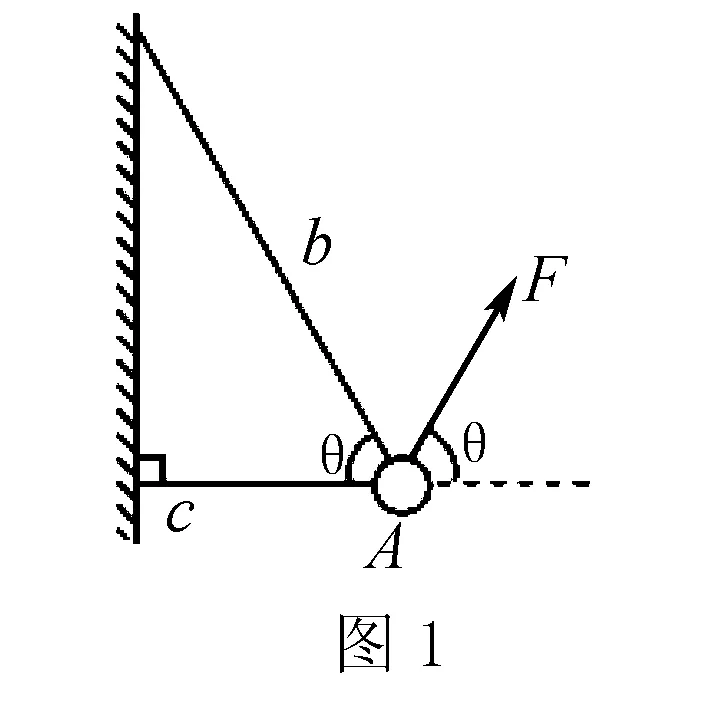
例1 如图1所示,物体A的质量m=2kg,两根轻细绳b和c的一端连接于竖直墙上,另一端系于物体A上,两绳的夹角θ=60°.在物体A上另施加一个与水平线也成θ角的拉力F,若要使两绳都能伸直,求拉力F的取值范围.(g取10 m/s2)
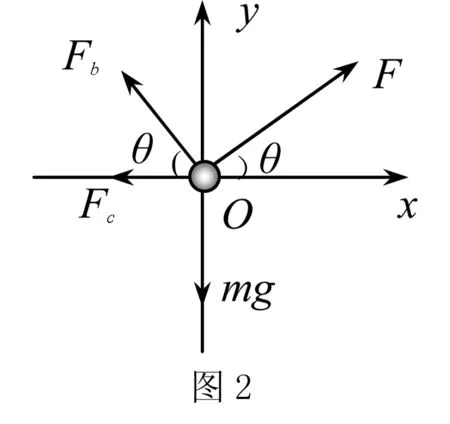
解法1 以小球为坐标原点建立如图2所示的直角坐标系,设b、c两绳上的张力大小分别为Fb、Fc,小球的受力如图2所示.
由力的平衡条件得:
(1)Fsinθ+Fbsinθ-mg=0
(2)Fcosθ-Fbcosθ-Fc=0
由(1)式知:当b绳刚好伸直即Fb= 0时,拉力F有最大值,
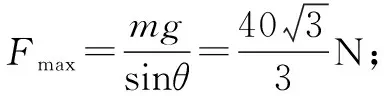
由(1)(2)式得:
(3)2Fcosθsinθ=mgcosθ+Fcsinθ
由(3)式知:当c绳刚好伸直即Fc=0时,拉力F有最小值,
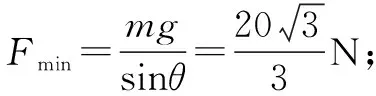
故拉力F的取值范围是:
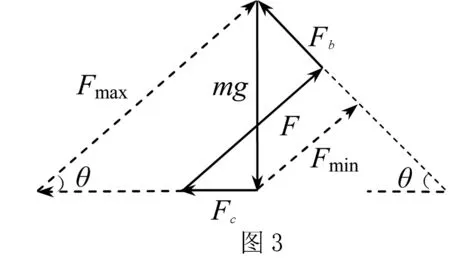

点评本题属于力的平衡中临界与极值问题.解法1用到了解析法,利用力的平衡条件列出相关变量的表达式,通过表达式来寻找问题的临界状态与极值,这是一种利用数学函数求物理极值问题的方法;解法2用到了图解法,通过力的矢量图形可以较简洁的找到问题的临界状态与极值,这种解法更体现了问题的物理本质.在定性分析动态平衡平衡问题时,图解法往往比解析法显得更直观、更简洁、更有效.
三、三类问题
1.静摩擦力、弹簧弹力作用下的平衡问题
平衡状态下的物体受到的静摩擦力可能存在两个相反的方向.弹簧对物体的弹力可以是拉力,也可以是压力,即弹簧对物体的弹力也可能存在两个相反的方向.因此在静摩擦力与弹簧弹力作用下物体的平衡,可能存在多种可能性,考虑到静摩擦力与弹簧弹力可能存在的方向,进行分类讨论.
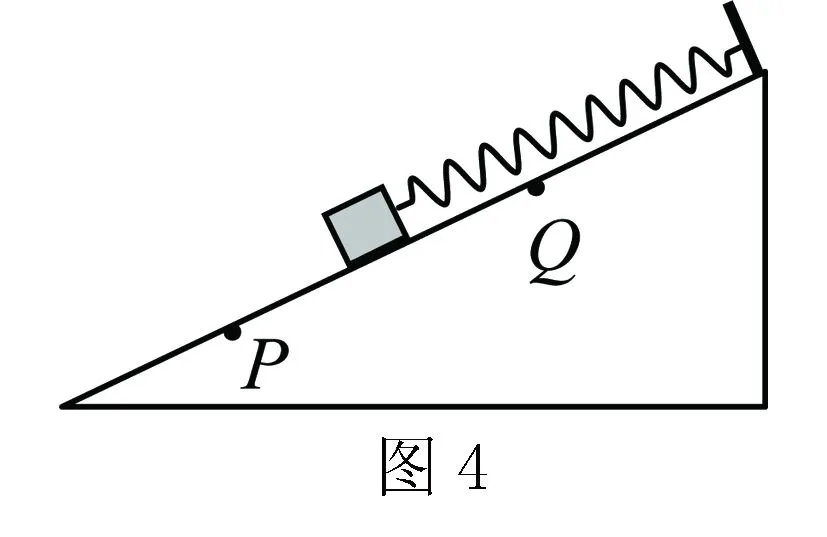
例2 如图4所示,劲度系数k=100N/m的轻弹簧上端固定在斜面顶端,下端挂一个小物体放在斜面上,弹簧的轴线与斜面平行.物体只能在斜面上的P、Q两点间的任何位置才能处于静止状态,已知物体与斜面间的最大静摩擦力Ffm=6N.则以下说法正确的是( ).
A.物体放在P点时,弹簧可能伸长,也可能压缩
B.物体放在Q点时,弹簧可能伸长,也可能压缩
C.P、Q两点间的距离x=0.12 m
D.斜面的倾角θ= 30°
解析由于物体只能放在斜面上的P、Q两点才能处于静止平衡状态,因此物体在在P、Q两点受的斜面的静摩擦力应为最大值Ffm,且在P点受到的最大静摩擦力方向沿斜面向下,因此在P点弹簧只能处于伸长状态;在Q点受到的最大静摩擦力方向沿斜面向上,因此在Q点弹簧可能处于伸长状态,也可能处于压缩状态;设物体质量为m,在P点弹簧伸长x1,由力的平衡条件有:kx1=mgsinθ+Ffm(1)
在Q点弹簧伸长x2,由力的平衡条件有:kx2=mgsinθ-Ffm(2)
P、Q两点间的距离x=x1-x2(3)
联立(1)(2)(3)式,代入数值解得:x=0.12 m;
若在Q点弹簧压缩x2,由力的平衡条件有:kx2+mgsinθ=Ffm(4)
P、Q两点间的距离x=x1+x2(5)
联立(1)(4)(5)式,代入数值解得:x=0.12m;
通过以上求解知,本题不能确定斜面倾角的值.
答案 BC
点评本题中力的平衡问题将斜面、静摩擦力与弹簧弹力相结合,物体在斜面上平衡时受到斜面的静摩擦力的方向可能沿斜面向上或向下,弹簧对物体的弹力的方向也有可能沿斜面向上或向下.由于物体在P点平衡时弹簧最长,这时弹簧一定处于拉伸状态;容易误认为在Q点平衡时弹簧最短,这时弹簧一定处于压缩状态;其实物体在Q点平衡时弹簧是拉伸还是压缩,应取决于物体和斜面间的最大静摩力Ffm与物体沿斜面方向重力分力mgsinθ的大小,因此需要进行分类讨论.
2.三力平衡问题
在求解三个共点力平衡问题中,若能灵活地运用拉密定理与三力汇交定理,可使问题的求解变得简洁.
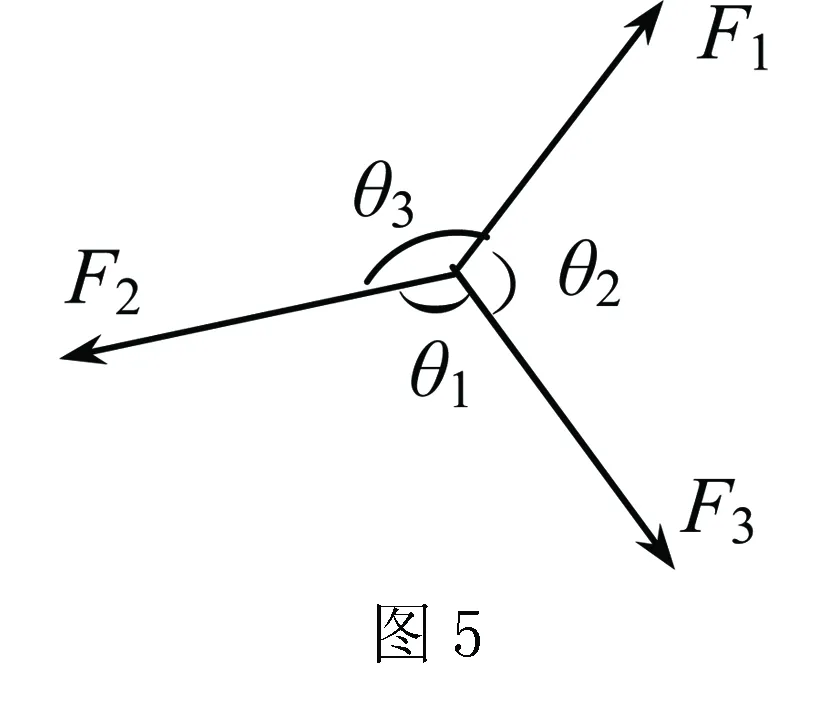
(1)拉密定理.如图5所示,当三个共点力处于平衡时,则每一个力和其它两力间夹角的正弦成正比,即:
(2)三力汇交定理.如果一个物体在三个力作用下处于平衡,若这三个力不平行,则这三个力的作用线(或延长线)必相交于一点.
例3 长为a的细线系于质量为m边长为a的正方体一条棱的中点,线的另一端固定在光滑竖直墙壁上(如图6),求线上的拉力FT及墙壁对正方体的支持力FN的大小.
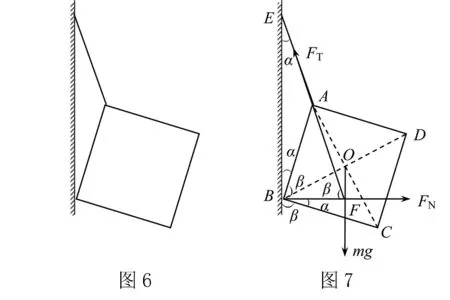
解析正方体受三个力作用处于于平衡,这个力分别是重力mg、绳子拉力FT、墙壁的支持力FN,显然这三个不平行,则这三个力的作用线必共点(如图7所示).在△BOF中,有:
在ΔABF中,BF=2acos(90°-α)=2asinα;则有:

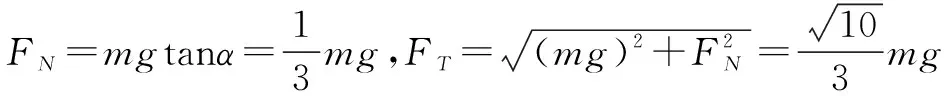
点评此题分析求解的关键是根据三力汇交定理作出图7所示的物体受力图,利用解析法结合相关的数学知识进行求解.
如果物体在多于三个共点力的作用下处于平衡,有时可以将其中的某些力先进行合成,可将物体等效为受三个力作用,从而能利用上述两个定理对问题进行分析与求解.
3.动态平衡问题
通过控制某些物理量,使物体的状态发生缓慢地变化,物体在这一变化过程中始终处于一系列的平衡状态中,这种平衡称为动态平衡.求解动态平衡问题的基本思路是化“动”为“静”,“静”中求“动”.
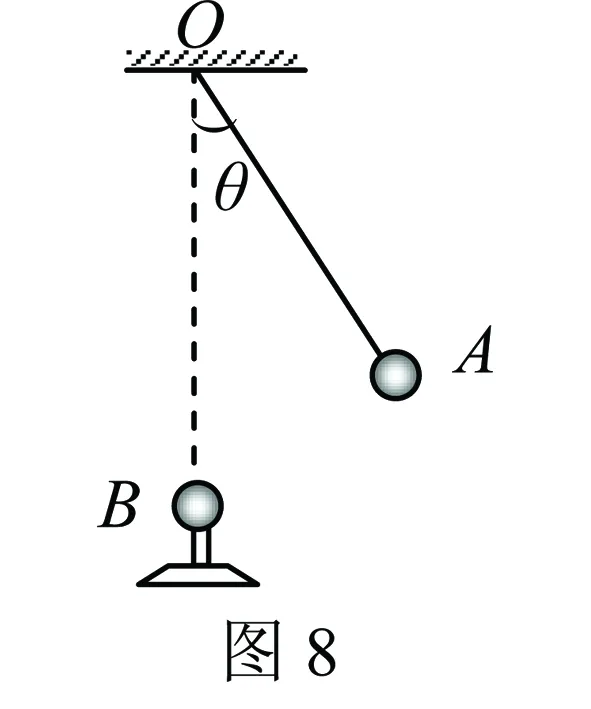
例4 如图8所示,一绝缘细线OA下端系一质量为m的带电的小球A,悬点O正下方有一带电小球B固定在绝缘底座上.开始时A球静止在图中位置,此时细线OA与竖直方向的夹角为θ.现将B球沿竖直方向缓慢上移一小段距离,在此过程中,下列说法正确的是( ).
A.细线OA与竖直方向的夹角θ保持不变
B.B球所受的库仑力一直变大
C.细线OA的拉力一直变大
D.A球与B球间的距离一直变大
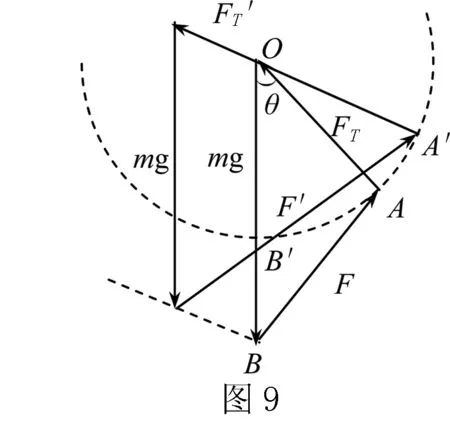
解析A球受到B球的库仑力F、绳子的拉力FT、重力mg,其合力为零,平移三个力矢量组成一个封闭的三角形.注意到mg不变,FT的方向总是过O点,F与FT的交点在以O点为圆心的圆周上移动,画出初态、末态的三个力矢量三角形(如图9所示).可知:F变大、FT变大、θ角变大.答案 BC
点评缓慢上移B球时A球会沿圆周缓慢上升,θ角变大;当B球移到与A球(改变后的位置)等高时,两球间的库仑力最大;若再继续上移B球时两球间的库仑力会减小,A球则会沿圆周缓慢下降,θ角就会变小(有可能减小到比开始的还小).