对一道高考数学卷压轴题的研究与反思

汤 斌

(广东省湛江第一中学 524038)

高考数学压轴题，是试卷中比较有代表性的题.大多数同学都认为压轴题是“拔高题”.压轴题不仅仅考查的是学生的数学学习能力以及应用能力，更考查的是学生的逻辑判断能力以及逻辑分析能力.在不同层次上的理性思维，也对学生的创新解题思维进行综合考查，给予优秀生一个展示能力的空间.

一、试题展现

题目已知函数f(x)=ae2x+(a-2)ex-x.

(1)讨论f(x)的单调性；

(2)若f(x)有两个零点，求a的取值范围.

本道题目是2017年数学高考全国一卷的二十一题，本题考查的知识点是函数单调性以及零点理论知识.这个知识点学生在平常练习中经常会遇到，解题思路大部分学生都能掌握，关键点在于思路的转换和计算能力.

二、试题分析

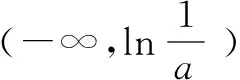
第(1)问中的解答的重点在于转化导数形式和分类讨论参数a，如果将函数进行因式分解，分类讨论参数a的问题将会迎刃而解，以大部分学生的解题能力，二次函数的因式分解不是本题的难点.一般高考压轴题的设定都是以课本为基础又高于课本，根据对历年高考压轴题的分析来看，函数的单调性是必考题，无论题型怎样变化，考查学生复杂函数的运算能力，进而对函数的单调性进行判断，所以运算能力是学生的必须掌握的一种能力.

(2)问的答题方法有两种，方法一是画出函数图形判断零点；方法二是进行函数转化.

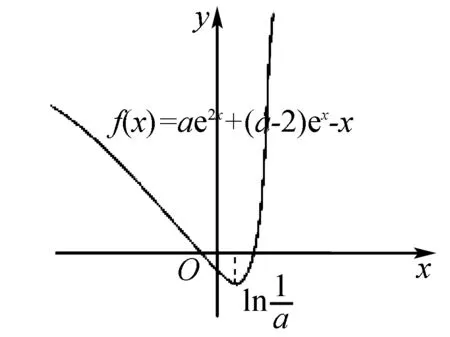
图1

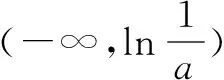
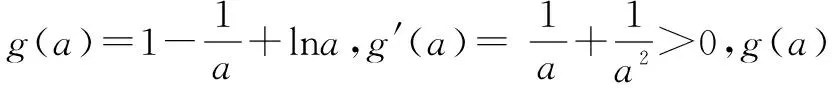
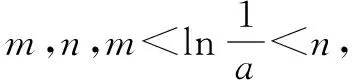
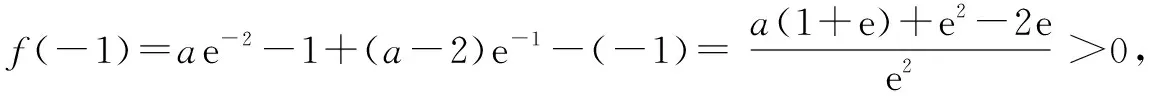
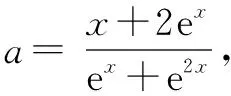
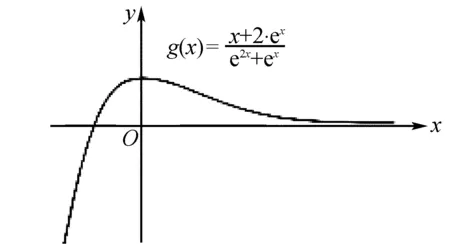
图2

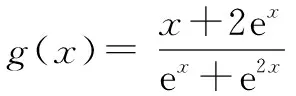
根据图象可得出0

压轴题是高考数学的难点也是得高分的关键，其中包含了重要的基础知识和数学思想，是高考考查中不可或缺的内容，其呈现方式灵活多变.思想方法考查在高考数学中至关重要，对思想方法的考查就是变相考查数学知识的扎实程度，思想方法的掌握程度决定了学生的分值范围.所以在剖析压轴题的过程中，要对学生渗透思想方法，对其中的知识进行归纳和总结，从而提升学生的数学水平和应试能力.