导数综合题中的切线研究
2019-02-15张弛
张 弛
(浙江省诸暨市海亮高级中学302班 311800)
在解决函数与导数相结合的综合题中,利用函数的图象来分析题目的结论,尤其是利用直线与曲线相切相关的一些结论,往往会使问题变得直观易懂,那么下面举例说明.
先来看2018年浙江省数学高考题压轴题:
(1)若f(x)在x=x1,x=x2(x1≠x2)处导数相等,证明:f(x1)+f(x2)>8-8ln2;
(2)若a≤3-4ln2,证明:对任意的k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.

曲线上的点(x0,f(x0))处从左到右的切线斜率的变化情况:-

由图象可知,当a≤3-4ln2时,直线y=kx+a与曲线有唯一交点.

从上面的分析可以看到,此题的命制完全是由曲线与直线相切而来.
从图象来看,下面的改编题中可以看得更清晰一点:
已知f(x)=-x3+9x2-26x+27.
已知对任意的k>0,直线y=kx+a与曲线y=f(x)有唯一公共点,求a的取值范围.
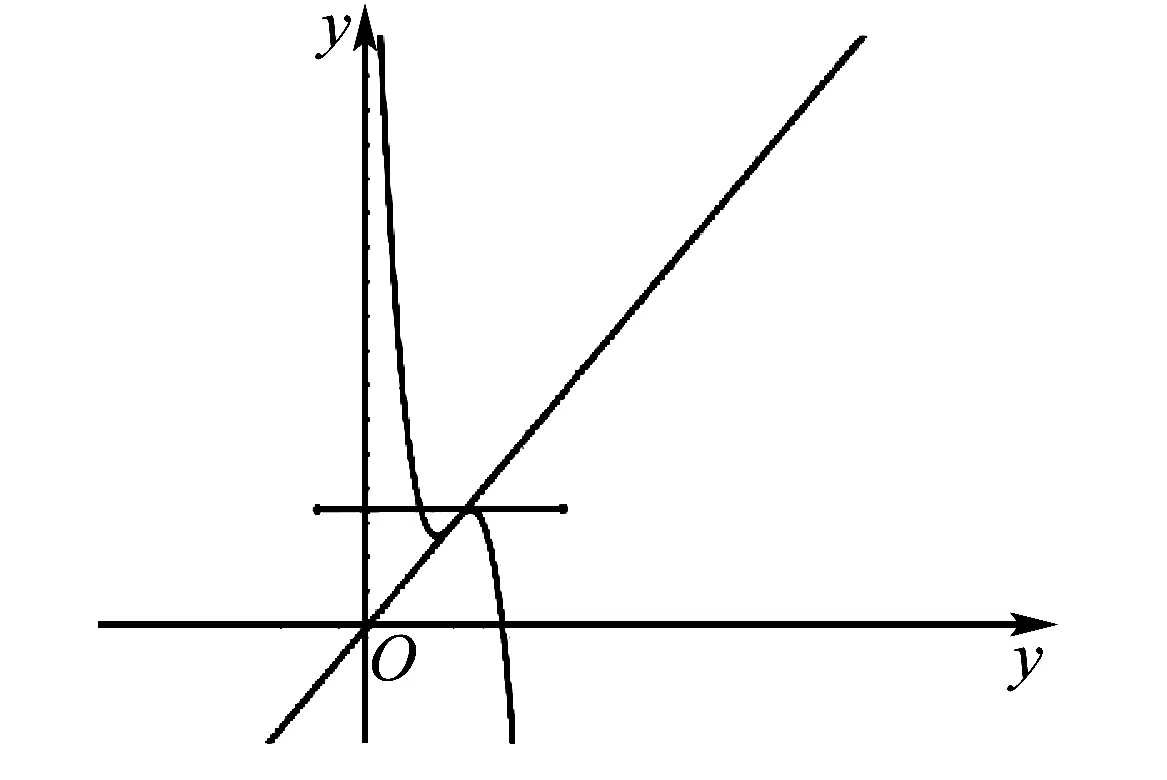

从此题可以看出,充分利用函数图象的切线,可以化繁为简,让问题变得直观明了,下面针对这种如何利用函数图象切线的问题做一个总结.
一、直接利用曲线与直线相切来设计的不等式恒成立问题
我们最常用的曲线的切线有指数函数的切线、对数函数的切线:
用不等式来表示即是:ex≥x+1;ex≥ex;lnx≤x-1.
例1 (2017·全国卷Ⅱ) 已知函数f(x)=ax2-ax-xlnx,且f(x)≥0.
(1)求a;
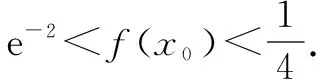
分析第(1)小题的要求可以等价地转化为a(x-1)-lnx≥0,即lnx≤a(x-1),我们发现就是研究曲线y=lnx的切线而已,因为lnx≤x-1,所以a=1.
(2006年全国Ⅱ理20)设函数f(x)=(x+1)ln(x+1),若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.
分析先根据导数画出原函数草图

因为曲线f(x)=(x+1)ln(x+1)在原点处的切线方程为y=x,所以结合图象及原点处的切线可知:实数a的取值范围为a≤1.
甚至可以借用切线来构造以下这样一个题目:
求证:ex≥2+lnx.
分析因为ex≥x+1,lnx≤x-1⟺x≥1+lnx,所以得证.
二、利用直线与曲线的位置关系来研究函数的零点或函数的极值点的存在性问题



当然以上问题的设计意图都比较明显,而且题中给出的函数一般不需要加以改造与变形,让我们比较容易想到利用函数图象结合切线的相关结论,但也有些问题需要先构造合适的函数,再利用切线的结论来解决问题,因此在解题分析过程中,观察表达式的特点及图象特点有助于分析问题能力的提升.

分析按常规方法分析,我们会遇到困难,因为其导数太奇怪了!





再看下例,充分利用了问题设计中的铺垫来引导我们利用曲线的切线来解决问题.
例4 (2015天津)已知f(x)=4x-x4.
(1)求f(x)的单调区间;
(2)设曲线y=f(x)与x轴正半轴的交点为P,曲线y=f(x)在点P处的切线方程为y=g(x),求证:f(x)≤g(x);


分析把该函数的图象在题中相关点的切线都求出来:
先求出导函数f′(x)=4-4x3.

从以上的例题可以看出,对于函数与导数相结合的综合题,如果充分利用函数的图象,尤其是利用函数图象的切线相关结论,可以使得问题的解决简单易懂,所以在以后的解题中要加以重视.