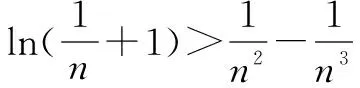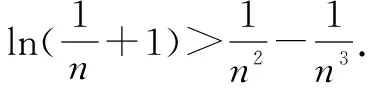构造函数证明不等式或命题
2019-02-15王中华
王中华
(山东省枣庄市第二中学 277400)
构造函数是解决导数问题的基本方法,在导数问题中, 常常需要根据条件构造函数,再根据条件得出所构造函数的单调性,应用单调性及最值等知识解决问题,该类题目具有一定的难度.有时简单的构造函数对问题求解带来很大麻烦甚至是解决不了问题的,那么怎样合理地构造函数就是问题的关键.这里我们来一起探讨一下这方面问题.
一、就函数解析式的部分因子构造函数
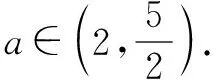

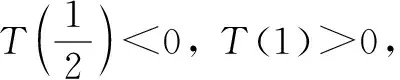
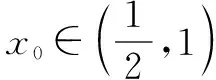
所以当x∈(0,x0)时,t′(x)<0,t(x)单调递减;
所以当x∈(x0,+∞)时,t′(x)>0,t(x)单调递增.
所以t(x)的最小值为t(x0)=ex0-lnx0-a=0.
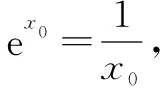
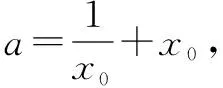
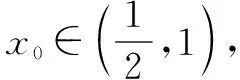
小结本题构造函数,求导,对导函数的分子再构造函数.研究曲线切线、函数图象的交点等解析几何问题,可以利用函数的值域或最值,结合函数的单调性、草图确定其中参数范围.从图象的最高点、最低点,分析函数的最值、极值;从图象的对称性,分析函数的奇偶性;从图象的走向趋势,分析函数的单调性、周期性等.利用数形结合的思想去分析问题,使问题的求解有一个清晰直观的整体体现.
二、构造差函数
例2 (2017内蒙呼和浩特一模)已知函数f(x)=ex-x2-1,x∈R.当x∈R时,求证:f(x)≥-x2+x.
分析构造差函数:g(x)=f(x)+x2-x,再利用导数求其最小值g(x)min=g(0)=0,即得证.
证明令g(x)=f(x)+x2-x=ex-x-1,
令g′(x)=ex-1=0,得x=0.
∴当x∈(-∞,0)时,g′(x)<0,g(x)单调递减;
当x∈(0,+∞)时,g′(x)>0,g(x)单调递增.
∴g(x)min=g(0)=0,从而f(x)≥-x2+x.
小结对于函数在某区间内函数值恒成立问题,可以用求函数最值的方法, 一般通过变量分离,将不等式恒成立问题转化为求函数的最值问题,然后再构造辅助函数f(x),利用f(x)>m恒成立⟺f(x)min>m;f(x) 证明对g(x)=xlnx求导,则g′(x)=lnx+1. 当0 当x>a时,F′(x)>0,因此F(x)在(a,+∞)上为增函数. 从而当x=a时,F(x) 有极小值F(a). 当x>0时,G′(x)<0,因此G(x)在(0,+∞)上为减函数. 小结对于本题绝大部分的学生都会望而生畏.学生的盲点也主要就在对所给函数用不上.如果能挖掘一下所给函数与所证不等式间的联系,想一想大小关系又与函数的单调性密切相关,由此就可过渡到根据所要证的不等式构造恰当的函数,利用导数研究函数的单调性,借助单调性比较函数值的大小,以期达到证明不等式的目的. 所以函数h(x)在(0,+∞)上单调递增,∴x∈(0,+∞)时,恒有h(x)>h(0)=0, 即x3-x2+ln(x+1)>0,∴ln(x+1)>x2-x3. 小结我们知道,当F(x)在[a,b]上单调递增,则x>a时,有F(x)>F(a).如果f(a)=φ(a),要证明当x>a时,f(x)>φ(x),那么,只要令F(x)=f(x)-φ(x),就可以利用F(x)的单调递增性来推导.也就是说,在F(x)可导的前提下,只要证明F′(x)>0即可.三、主元法构造函数



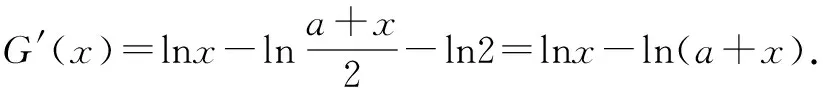
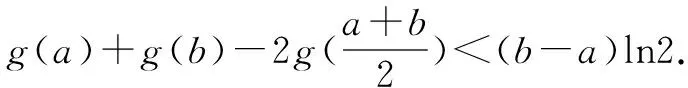
四、换元法构造函数