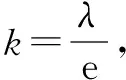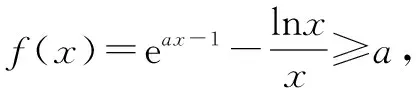一种新思路下的导数题妙解

陈浩良

(福建省福安一中 355000)

例1 已知f(x)=x-1-lnx，g(x)=ex-ex.若在[1,+∞)上恒有g(x)≥λf(x)成立，试求λ的取值范围.

这里先给出此题的常规解法.

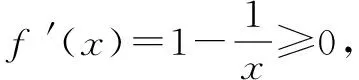
故f(x)≥f(1)=0，当且仅当x=1时取等号.

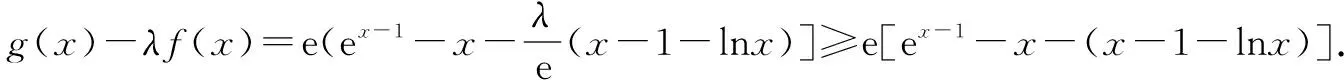
显然在[1,+∞)上h″(x)≥h″(1)=0，故在[1,+∞)上h′(x)单调递增,所以h′(x)≥h′(1)=0，故在[1,+∞)上h(x)单调递增，故h(x)≥h(1)=0，所以有g(x)-λf(x)=eh(x)≥0，即g(x)≥λf(x)在[1,+∞)上恒成立.

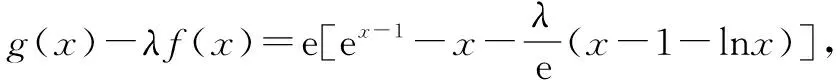
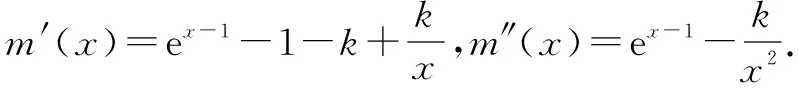
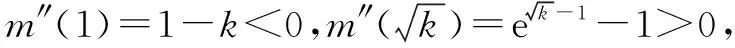
则m(x)在(1,x2)上单调递减，在(x2,+∞)上单调递增.因为m(1)=0所以m(x2)

所以x=x2时g(x2)-λf(x2)=em(x2)<0不合题意.

综上所述，λ的取值范围为(-∞,e].

从上述解法中，我们可以看出，e这个分类讨论的分隔点出现的很突兀，而且在第ii)分类是由于求了二阶导数，解题过程十分繁杂，而且要说清楚较为困难.在此本文根据一个很基本的常识x=elnx给出在新思路下的解法

则g(x)≥λf(x)⟺ex-1-k(x-1)≥elnx-klnx⟺n(x-1)≥n(lnx).

若k≤0则n′(x)=ex-k>0，故n(x)在[1,+∞)上单调递增.

即x-1≥lnx，所以n(x-1)≥n(lnx).

若k>0，令n′(x)=0，得x=lnk，

所以n(x)在(-∞,lnk)上单调递减，在(lnk,+∞)上单调递增.

1)若0

2)若k>1,令x0-1=lnk，此时x0≠1因为x-1≥lnx当且仅当x=1时取等,

故此时x0-1=lnk≠lnx0，所以n(x0-1)=n(lnk)=n(x)min

综上所述，k的取值范围为(-∞,1]，故λ的取值范围为(-∞,e].

比较上述两种解法，显然在新思路下的解法更为简明，分类标准更为清晰，说明过程也显得不啰嗦.哪种解法更为高明？答案显而易见.

例1中不用新思路解题其实也能完成解答，但是倘若碰到一些常规解法没有办法解决的题目，又该如何呢.下面我们再看另一题新思路速解.

倘若按照一般思路对f(x)进行求导，那么你会发现

看，只通过一个基本结论就将问题简化至这样，新思维的优越又一次体现.故，在解题中运用常见结论，简化问题便是新思维新思考的本质所在.当然，新思路自然不止这一种，更多的新思路有待解题过程中你们自己去发掘，记住，别被惯性思维限制.