关于向量与三角形“四心”一类问题的研究

庞嘉鹏

(辽宁省铁岭市高级中学三年25班 112000)

根据向量的数形特性,我们可以将三角形数量化,并通过运算化简来解决与三角形“四心”有关的轨迹等问题.本文研究一些有关向量与三角形的“四心”知识交汇的相关问题，以帮助同学们更好地体会向量的独特魅力.

一、向量在三角形“重心”中的应用

三角形重心是三角形三条中线的交点，并且重心到顶点的距离与重心到对边中点的距离之比为2∶1.在三角形重心的研究中，我们可以结合向量的中线形式或平行四边形法则，用向量共线来研究动点轨迹过三角形重心的问题.

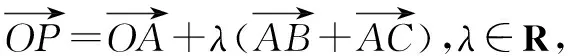
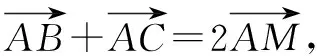
点评本题主要是通过运用三角形法则和平行四边形法则以达到向量共线的目的，再结合三角形重心定义，得出正确的结论.

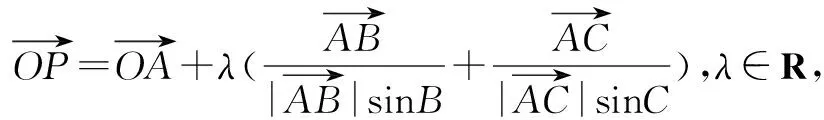
点评本题巧妙地运用了正弦定理，使该题等价变形为例1的形式，从而解决问题，所以熟悉例1的题型是解决这类问题的基础.

二、向量在三角形“内心”中的应用

三角形的内心是指三角形的三个内角平分线的交点，即三角形内切圆的圆心.本类问题主要是通过单位向量和向量的平行四边形法则构造一个菱形，再利用菱形对角线就是角平分线和向量共线的性质，从而解决了动点轨迹过三角形内心的问题.

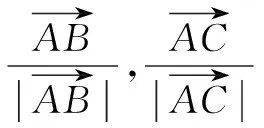
点评本题的关键是熟悉单位向量的形式，通过向量的平行四边形法则构造出一个菱形，再结合向量共线、内心定义，从而解决这类知识的交汇问题.

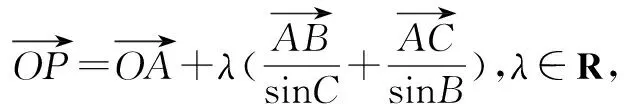
点评本题结合了正弦定理，使该问题实现了等价转化，从而变成了例2的形式，问题得以解决.所以熟练掌握例2的题型是解决这类的关键.

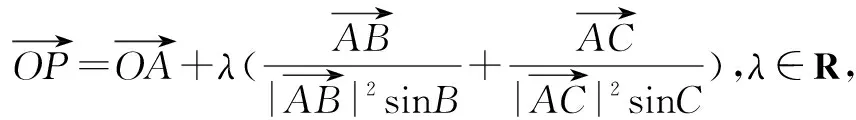
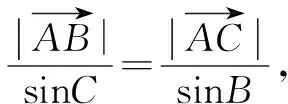
点评本题形式比较复杂，不容易找到解决问题的突破口，解决此类问题还是要等价转化，这里两次运用了正弦定理，先后转化为上述变式1例2的题型.

三、向量在三角形“垂心”中的应用

三角形的垂心是三角形的三条高或其延长线的交点.利用向量研究直线或线段的垂直问题是比较方便的，关于直线垂直问题就可以转化为向量的数量积为零的问题，此时向量的优越性就非常明显地体现出来.两个向量垂直的充要条件可以把“垂直”的内在含义淋漓尽致地体现在一个等式中，有效地回避了解析几何中错综复杂的位置关系的演化，而变为纯粹的化简运算，通过这种思想来解决动点轨迹过三角形垂心的问题还是比较方便的.

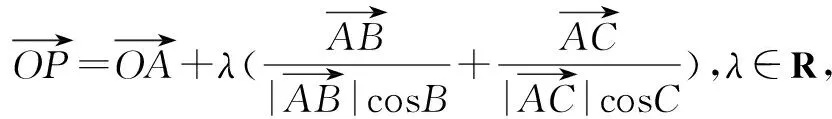
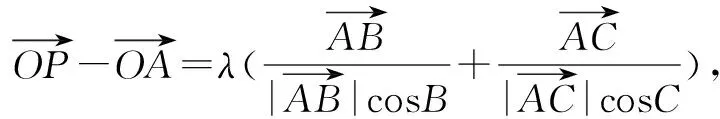
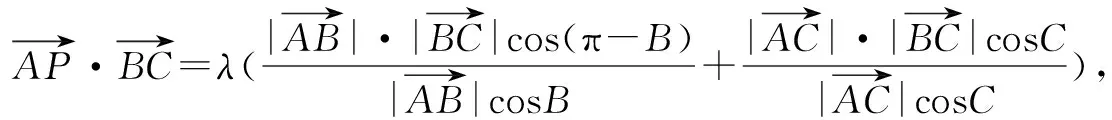
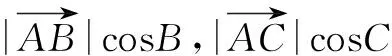
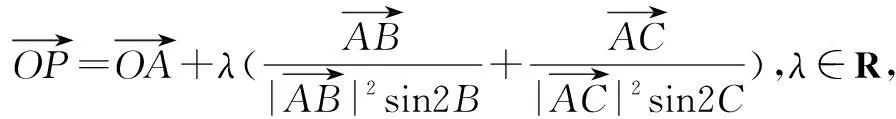
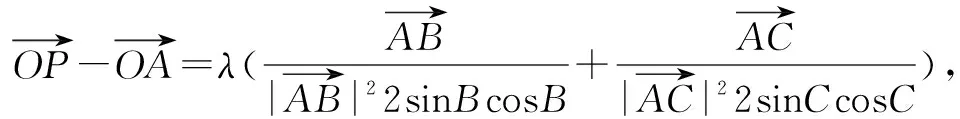
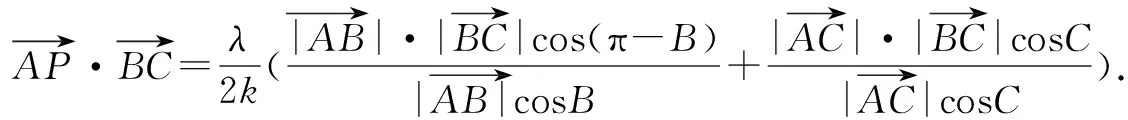
再由三角形垂心的定义可得动点P所在的轨迹一定经过△ABC的垂心.

点评本题的切入点不易发现，首先运用了倍角公式变形，发现一部分条件属于正弦定理问题，通过应用正弦定理，使该题型转化成例3的题型，所以掌握例3是解决过垂心的问题的关键.

四、向量在三角形“外心”中的应用

三角形的外心就是三角形三边垂直平分线的交点，三角形的三个顶点就在这个外接圆上，即三角形外接圆的圆心.用向量研究外心问题，主要还是要结合外心定义和向量垂直问题来共同解决动点轨迹过外心的问题.

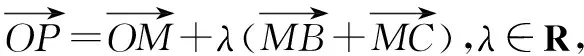
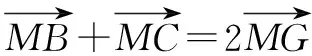
点评本题难度适中，主要考察了垂直平分线定义、外心定义，通过三角形法则、平行四边形法则达到向量共线的目的，使问题得以解决.

在以上的问题中，向量通常是几何的形式出现的， 用向量作为工具对于解决几何问题有其独到之处，将传统几何中的定性推理转化为代数运算化简的定量分析，避免了传统几何方法中繁琐的推理及论证，充分体现出数学中数与形这二元结合、相辅相成的基本内涵和本质特征，为高中数学增加了活力.