加强数学命题 证明数列不等式

刘佳雪

(河北师范大学附属中学 050011)

高考对数学归纳法的考查最常见的是用数学归纳法证明数列不等式.这虽然是一个行之有效的基本证题方法,但有时会发现有些数列不等式如果一边是常数，在证从“k”到“k+1”的过程中，递推过程将无法实现，不能证明命题P(n).此时，我们可以通过证明一个比命题P(n)更强的命题，来达到证明命题P(n)的目的.下面我们给出两个例题来说明，探究如何解决这类问题.

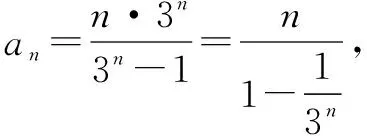
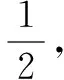
当n=1时，显然成立.

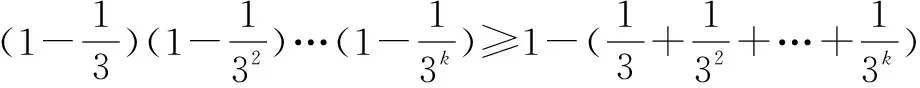
那么，当n=k+1时，

所以①式成立，从而结论得证.

当n=1时，原不等式成立.

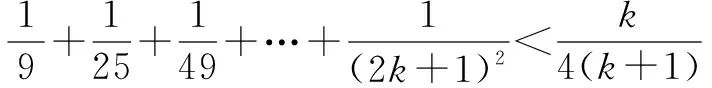
那么，当n=k+1时，

所以当n=k+1时，不等式③成立，

评注由于归纳假设也随之加强，这样强化的命题也更易于归纳法证明.

说明通过以上两个例题我们发现，解决不等式问题的关键是如何加强命题，望同学们多做一些类似的题目，体会方法.