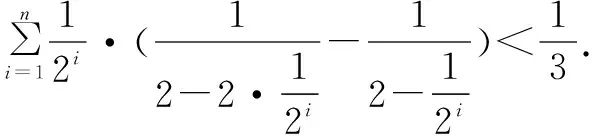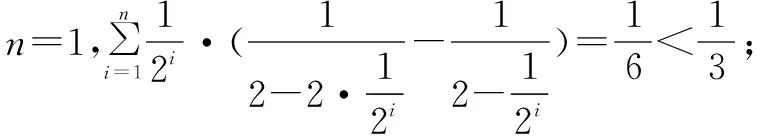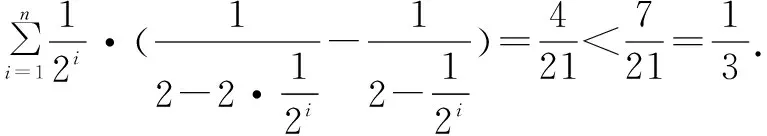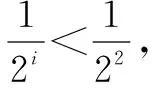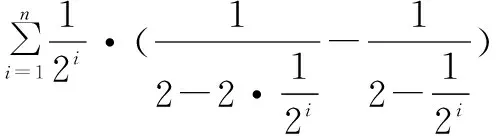探究过度放缩后的一种 “修正术”

江凤华 江国荣

(1.江苏省无锡市辅仁高级中学高三9班 214123； 2.江苏省无锡市市北高级中学 214045)

一、探究过程

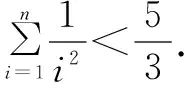
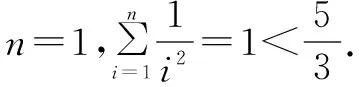
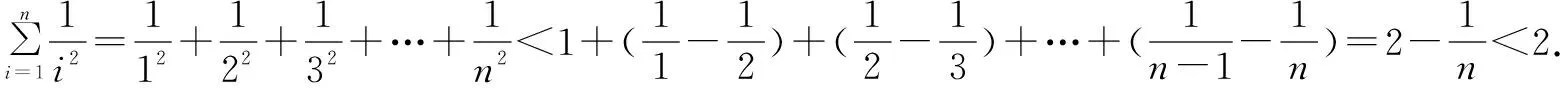
结果发现放缩过度，原因是每一步放缩的“步幅”大了，减小“步幅”后再试.

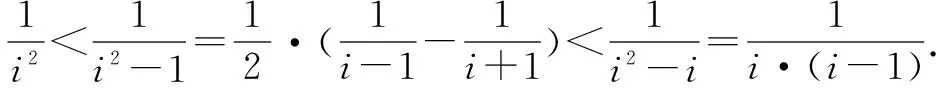
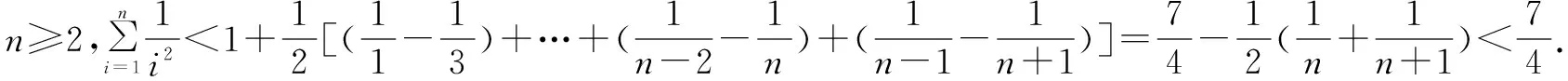
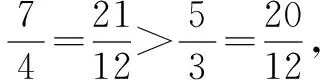
下面笔者做进一步探究：

试证3 若保留前两项不放缩(易先证明n=1,n=2满足条件)，当n≥3时，

初探感受：(试证3)中通过保留两项，减少放缩项数，起到了一定的缩小性调节作用，受此启发，对(试证1)也进行逐步留项探究： 如果保留前两项不放缩,

分别再保留前三、前四、前五项不放缩，结果依次为：

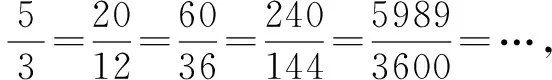
二、小结：根据傅立叶级数展开式

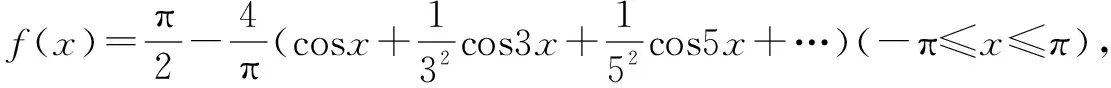
笔者认为：证明此类收敛性数列求和不等式，所证明的目标如果与无穷级数的和有一定的距离的话，若找到了一种可求数列和的放缩方法，即使发现放缩过度(包括放大过度和缩小过度)了，也可在不改变原来的方法基础上采取逐步保留前几项不放缩(相当于增加保真项)的办法减小偏差，这种探求证明过程笔者称其为顺藤留瓜，瓜不熟不摘式,留项累加后再放缩法.

三、方法应用对比举例