数学思想在数列问题中的应用举例

李一诺

(河北省邢台市第二中学2016级18班 054000)

一、利用方程思想解题

方程思想充满了数列整个章节，它是解决数列有关元素问题的基本方法，运用方程思想解题需要抓住基本量，掌握好设未知数，列方程，解方程三个环节.

例1 等差数列{an}的前m项和为30，前2m项和为100，则它的前3m项的和为( ).

A.130 B.170 C.210 D.260

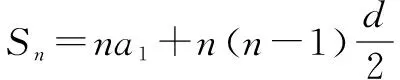
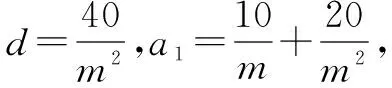
二、利用函数思想解题

数列是特殊的函数，因此，求解数列问题应根据题意注意沟通数列与函数之间的内在联系，运用函数的思想方法求解往往使解题方便快捷.

例2 在等差数列中，已知Sp=q,Sq=p(p≠q)，求Sp+q的值.

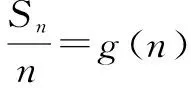
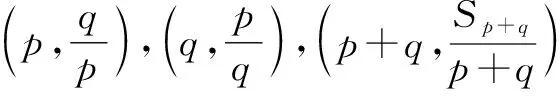
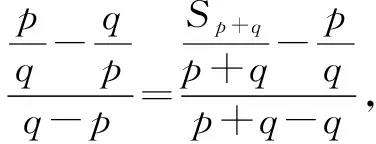
三、利用分类讨论思想解题

依据题中的条件，确定讨论对象和讨论标准，使用分类讨论思想，使解题更具有条理性，解题过程更加清晰.

例3 求和Sn=1+2x+…+nxn-1(x≠0).

解∵Sn=1+2x+3x2+…+(n-1)xn-2+nxn-1,

∴xSn=x+2x2+…+(n-1)xn-1+nxn.

两式相减得(1-x)Sn=(1+x+x2+…+xn-1)-nxn.

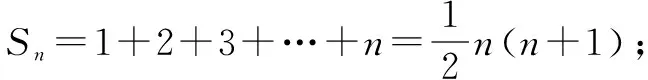
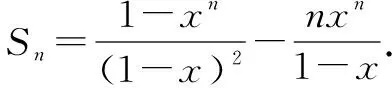
四、利用转化思想解题

根据题目所给的结构特征，寻找项之间的规律，利用转化思想解题.它集中体现在求和过程中将非特殊数列转化为等差数列或等比数列.

例4 求和Sn=1·2+2·3+3·4+…+n(n+1).

解∵k(k+1)=k2+k(k=1,2,…,n),

∴Sn=(12+1)+(22+2)+…+(n2+n)

=(12+22+…+n2)+(1+2+…+n)

五、利用数形结合思想解题

恩格斯曾经这样定义数学：“数学是研究现实世界的量的关系与空间形式的数学”.数形结合不仅是一种重要的解题方法，而且也是一种重要的思维方法.它形象、直观，有利于我们解题.

例5 设等差数列{an}的前n项和为Sn，已知a3=12,S12>0,S13<0,

(1)求公差d的取值范围;

(2)指出S1,S2,S3,…,S12中那一个值最大？并说明理由.

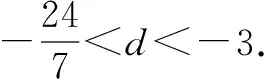
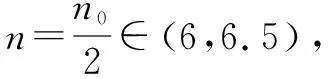
六、利用构造思想解题

构造法解题可以化繁为简，它主要体现在利用原数列构造新数列求通项的问题.

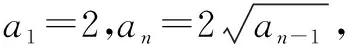
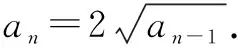
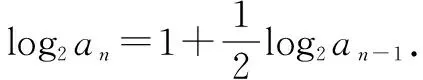
∴an=22-(1/2)n-1.