“积分变换”课程的教学改革探索
2019-02-15吴克坚赵清波徐清华梁锐华
吴克坚 赵清波 刘 烁 徐清华 梁锐华
(空军军医大学基础医学院数理教研室 西安 710032)
“积分变换”是工科相关专业一门重要的数学基础课程。对于我校生物医学工程专业来说,“积分变换”既是工程数学教学体系(“线性代数”、“概率论与数理统计”、“复变函数”与“积分变换”)中不可或缺的一环,作为解决实际问题的有力工具,也是该专业学员学习“电路理论”、“模拟电子技术”、“信号与系统”等多门后续专业课的基础,因此,学好这门课程对学员来说十分重要。但是“积分变换”具有理论晦涩难懂、知识点多、逻辑推理严密等特点,学员普遍认为该课程枯燥无趣、难学难记、学得辛苦却没什么效果;部分学员学习积极性不高,甚至产生畏难和抵触情绪。同时由于新的人才培养方案提出:工程数学要理论联系实际,提高工程应用能力等,也对“积分变换”的学时进行了压缩。针对这一矛盾,很多教师做了深入的研究和分析,提出了许多教学方法改革和教学内容优化的意见和建议[1~3]。借鉴这些教学改革的成果,结合我们学校的实际情况和近5年的教学实践,下面从几个方面谈谈我们的具体做法和思考,希望与广大教师一起探讨,目的是让学员对“积分变换”课程产生兴趣并在有限的时间内高效地学好这门课程,最终提升教学质量。
1 巧妙设计引入,调动学员的学习兴趣


引入单位脉冲函数δ(t)时,我们首先通过实例:“在原电流为0的电路中,某一时刻进入一单位电量的脉冲,如何确定该电路中的电流”以及如何描述力学中瞬间作用的冲击力、数字通信中的抽样脉冲等。因为之前学过的函数类中找不到一个函数能够描述这些集中于一点或一瞬时的物理量,因此需要引入一个新的函数,这个新的函数就是英国理论物理学家狄拉克(P.A.M. Dirac)提出的单位脉冲函数δ(t);其次强调由于许多常用函数如常数函数、幂函数、三角函数及指数函数等在区间(-,)上不满足绝对可积的条件,不能用Fourier积分公式直接求Fourier变换,因此数学上需要引入单位脉冲函数δ(t)解决常用函数Fourier变换的问题。这样设计的引入既强调了单位脉冲函数的重要性和意义,还降低了从数学概念上理解的难度。

2 强调内容的应用性,加强与后续专业课的联系
通过积分变换的学习,学员不仅应该掌握该课程的基本概念和基本理论,而且应该掌握积分变换在后续专业课程中的应用,因此我们选取了专业教学中的部分工程应用案例,结合工程背景把Fourier变换的性质、卷积等内容与这些实际案例融合在一起,对其中的概念、性质及理论的运用从工程化的角度进行分析和阐述,减少概念及理论的抽象性,解决数学理论和专业课相脱节的问题,提高学员的积分变换工程应用能力。
例如在讲解Fourier变换的卷积时,我们增加了“卷积的物理意义”这部分内容。选取的实际案例是:如何从收到的实际信号中分离出想要的某个频带内的信号或者如何从收到的信号中消除在传输过程中加入的高频干扰噪声。该案例转化成统一的问题就是:设信号函数f(t),如何对其进行理想低通滤波,即把该信号的低频成份完全保留,高频成份完全去掉。


“卷积的物理意义”这部分内容既复习了Fourier变换的物理意义,加深了卷积定理的理解,又突出了理想低通绿宝的积分变换原理,而且不用增加太多的课时就能让教学变得生动,让学员看到学以致用的魅力,起到事半功倍的效果。

3 及时总结归纳,有针对地处理难点
“积分变换”课程内容中常常出现一些学员不太容易理解和把握的知识点,如果没有及时总结讲解剖析,则容易在一定程度上造成学员学习积极性的降低和学习兴趣的下降,学习效果就会大打折扣。比如Laplace变换的频域微分性质、延迟性质等,必须花较多的学时深入讲解,多举例题,使得学员深刻理解。
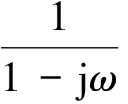

总之,根据“积分变换”课程特点与我校生物医学工程专业的需求,我们按照上述做法,在实际的教学过程中改进了教学方法、优化了教学内容,在现有的有限课时内不需要降低定理和理论证明方面的课时分配,也能够加强实践教学与理论教学的结合,提高了学员的学习兴趣,提升了“积分变换”课程的教学质量,得到了专业教师的认可,达到了预期的教学目标。
