关联关系粒化结构的矩阵计算与应用

2019-02-15毛华,武秀

小型微型计算机系统 2019年2期

毛华,武秀

(河北大学数学与信息科学学院,河北保定 071002)

1 引言

随着时代的发展,信息更新速度不断地加快.数据处理已成为问题解决的前提.因此,如何更好地进行数据的处理以解决实际问题已经成为颇受关注的问题.目前,计算机网络系统与工具体系不断发展完善,为了节省数据处理所需人力物力,可将数据处理问题转化成计算机可处理的问题.在知识发现研究领域中,图论[1,4]与粒计算[2,3,5]均为数据分析处理的有效方法.基于图论知识中图与矩阵产生的一一对应关系,可将以图为模型所讨论的问题转化为矩阵进行处理,从而将所处理问题归结为计算机方式解决,加快了问题的解决;粒计算是由Zadeh于1979年提出的概念[2].基于粒计算理论,可将数据集划分为粒,每个粒则可作为一个整体进行分析.在将关联关系作为考虑对象的情况下,每个关联关系则可看作单独的粒.因此,关联关系的合并可借鉴粒计算中粒处理的思想.

在数据合并问题的研究中,刘云生、李博[6]在时态数据库中二维数据的合并问题中提出一种时态数据模型及基于此模型的消除时态数据冗余的算法;并且在用图论模型与粒计算相结合的研究中,闫林、刘涛等[7]探究了基于无向图及其关联矩阵的数据合并问题,给出了关联组合结构与粒化结构的矩阵表示及其两矩阵的转化方法;闫林、高伟等[8]探究了基于有向图及其关联矩阵的数据合并问题,给出了加权粒化结构的矩阵表示与关联组合结构相应矩阵向其转化的方法.

然而上述文献均是考虑对数据的合并问题,在实际问题中,有许多情况是需要考虑关系的合并问题.例如:某城市考虑对公路资源分配给各调度站点的问题,如何解决路线的合并对各调度站点设置及资源分配的影响是一个具有现实意义的问题,该问题即为对于关联关系的合并而引发的问题的考虑.

对应的模型为:构造以每个调度站点作为顶点,各调度站点间存在的路线作为边的无向图,在某几条路线进行合并后,需要考虑调度站点如何调整、调度资源如何分配.

上述问题对应的数学模型为:以某城市为例,u1,u2,…,um分别表示该市内m个调度站点,两个站点间有公路可达时用一条线将其连接,记为ei,例如ei=(ui,uj)表示调度站点ui与调度站点uj间存在路线ei,记调度站点间存在的所有路线为e1,e2,…,ek.因此,调度站点与路线即构成以调度站点为顶点,站点间路线为边的无向图,并将调度站点的全体记为U,站点间公路路线的全体记为S.现在,市政府打算对路线进行规划,部分路线将被合并,即S被划分为E1,E2,…,En等n个部分,探究在路线进行合并调整后,调度站点如何调整、调度资源如何分配.该问题同样存在于航线及铁路路线合并问题中.路线就是两顶点之间的关联关系,也就是说,这类问题事实上是考虑关联关系的合并问题.

为了解决此类问题,本文对关联关系的合并对数据集的影响问题进行了分析.

本文结构如下:第2节给出一些基础知识;在第3节首先给出与关联关系划分相关理论的分析,其次,给出关联组合结构与粒化结构的矩阵表示与联系,之后,总结关联关系合并问题模型的处理过程,最后通过实例说明方法的正确性;第4节为结束语.

2 基础理论

定义1[1].设F为一个无向图,B(F)=(bij)ν×ε称为F的关联矩阵,其中v=|V(F)|,ε=|E(F)|,

(1)

V(F)={v1,v2,…,vν},
E(F)=(e1,e2,…,eε).

定义2[7].设P=(U,S,G)是关联组合结构,令S*={(Gi,Gj)|Gi,Gj∈G,Gi≠Gj且存在u∈Gi,及v∈Gj,使得(u,v)∈S},称S*为粒化关系,此时S*是G上的关系,即S*⊆G×G,并将G和S*组成的结构记作P*=(G,S*),称P*=(G,S*)为P=(U,S,G)的粒化结构.

定义3[9].设A,B为集合,用A中的元素x作为第一元素,B中的元素y作为第二元素,构成有序对,所有这样的有序对组成的集合,叫做A与B的笛卡尔积,记作A×B.即A×B={|x∈A,y∈B}.

当R⊆A×B时,则称R为从A到B的二元关系.

定义4[10].设U为数据集,C={X1,X2,…,Xn}(n≥1),其中Xi⊆U,Xi≠φ,Xi∩Xj=φ,其中i≠j,i,j=1,…,n,且∪Xi=U,则称C是数据集U的划分.

定义5[11,12].设U为数据集,S是U上的反自反关系,G={G1,G2,…,Gn}是对U的划分,则:

1)由U和S组成的整体称为关联结构,记作T=(U,S),并称S为关联关系.

2)由U、S和G组成的整体称为关联组合结构,记作P=(U,S,G),且仍称S为关联关系.

3 关联关系划分结构的探究

本节首先给出与关联关系划分相关理论的分析,其次,给出关联组合结构与粒化结构的矩阵表示与联系,之后,总结关联关系合并问题模型的处理过程,最后,利用上述理论探究了路线合并引起的调度站点调整问题.

3.1 关联关系组合结构及粒化结构的定义

本节采用数据合并的处理思想,将关联结构与关联组合结构引入关联关系的合并问题中.为此,先给出基于关联关系的两种结构的定义.

定义6.设U为数据集,S是U上的关系,E={E1,E2,…,En}是S的划分,则:

1)由S和U组成的整体称为关联结构,记作T=(S,U),并称U为关联数据集.

2)由S、U和E组成的整体称为关联组合结构,记作P=(S,U,E),且仍称U为关联数据集.

定义7.设P=(S,U,E)是关联组合结构,令U*={(Ei,Ej)|Ei,Ej∈E,Ei≠Ej且存在ei∈Ei,ej∈Ej,使得ei∩ej∈U},称U*为粒化关系,此时U*是E上的数据集,即U*⊆E×E,并将E和U*组成的结构记作P*=(E,U*),称P*=(E,U*)为P=(S,U,E)的粒化结构.

根据上述定义可知,E为关系S的划分,ei∩ej∈U表示边ei与ej有公共顶点,且该顶点属于U.

对于粒化数据集U*与数据集U来说,当ei∈Ei,ej∈Ej,Ei∩Ej∈U*当且仅当存在ei∩ej∈U,其中ei∈Ei,ej∈Ej.粒化数据集U*的产生是由于对关联关系S进行了划分,对于划分E={E1,E2,…,En}来说,每一个Ei被看作一个整体,是对关联关系S的一个合并;从关联组合结构P=(S,U,E)到粒化结构P*=(E,U*),则产生了由数据集U到粒化数据集U*的过程,实际上是对数据集U的重组过程.当关联关系间存在公共顶点时,则对于所属划分间同样能得到公共点,且该公共点属于粒化数据集U*.

与上面给出的数学模型相对应,其中调度站点的全体即为数据集U,路线的全体即为关联关系S,路线的合并情况则构成了路线的划分情况E.因此,基于S、U、E即可得到相应的关联结构T=(S,U)与关联组合结构P=(S,U,E).当路线的划分Ei与Ej中的边之间具有公共顶点(即与同一调度站点相关联),则可将满足该条件的所有站点进行重组,得到对数据集的粒化U*.路线的划分与调度站点的粒化组成了关联组合结构的粒化结构.

从粒计算角度考虑,关联关系的合并产生了关联关系的划分粒,粒化结构中U*是对原有数据集U的粒化.基于粒计算理论,从关联组合结构P=(S,U,E)到粒化结构P*=(E,U*),即通过关联关系的合并得到了数据集的重组以及划分粒与数据集粒间的关系.

例1.设P=(S,U,E)是关联组合结构,其中:U={1,2,3,4},S={(1,2),(2,3),(2,4),(3,4)},E={{(1,2)},{(2,3),(3,4)},{(2,4)}},我们记S={e1,e2,e3,e4},e1=(1,2),e2=(2,3),e3=(2,4),e4=(3,4),则E={{e1},{e2,e4},{e3}}.首先,因为边e2,e4进行了合并,所以数据集U*中则不再包含顶点3.其次,由于e3与e2具有公共顶点2,则在粒化结构中,{e3}与{e2,e4}具有公共顶点2;由于e3与e4具有公共顶点4,则在粒化结构中,{e2,e4}与e3具有公共顶点4;并且由于e3=(2,4),所以,{e2,e4}与e3均与顶点2和顶点4相关联.因此,{e2,e4}与e3称为平行边.e1与顶点1和顶点2相关联,{e2,e4}与顶点2和顶点4相关联,所以,{e2,e4}与e1具有公共顶点2.最后,可得粒化结构P*=(E,U*),其中E={{(1,2)},{(2,3),(3,4)},{(2,4)}},U*={{1},{2},{4}}.

3.2 关联组合结构与粒化结构的矩阵表示

以调度站点为顶点,调度站点间的路线为边,可构成图.并且从图论知识可知,图与矩阵产生对应关系,由一个图的关联矩阵可画出该图;同样地,通过一个图,相应的关联矩阵也可写出.因此,本节给出关联组合结构与粒化结构的关联矩阵定义,将结构分析转化为矩阵分析,加快问题的解决.

定义8.设P=(S,U,E)为关联组合结构,其中S={e1,e2,…,ek},U={u1,u2,…,um},E={E1,E2,…,En},且关联关系S根据划分E顺序排列.构造矩阵M(P),其中矩阵的行是关联关系S中任一边,列为数据集U中数据点.即:M(P)=(bij)k×m为关联组合结构P=(S,U,E)的关联矩阵,其中:

(2)

由于每一边与两个端点相关联,因此在矩阵M(P)中每一行中只含两个1.

对于例1中的例子来说,相应的关联组合结构P=(S,U,E)对应的关联矩阵为

(3)

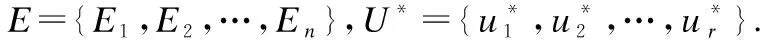
(4)

由于关联组合结构与粒化结构相对应,因此基于关联组合结构对应的关联矩阵M(P)可依据运算得到粒化结构相对应的关联矩阵M(P)*.

由于一个端点可与多条边相关联,因此对于矩阵M(P)的每一列可包含多个1,但每一行有且只有两个1.因此,对矩阵M(P)的前η行行向量(b11,b12,…,b1m),(b21,b22,…,b2m),……,(bη1,bη2,…,bηm)来说,若其合并,则其粒化结构中相应划分对应的行向量为((b11+b21+…+bη1)mod(η),(b12+b22+…+bη2)mod(η),…,(b1m+b2m+…+bηm)mod(η),其中amod(b)表示a除以b所得余数.为考虑节省存储空间,对于列零向量连与其对应的数据集进行删除,合并列向量相同的数据点.因此对于例1中相应粒化结构的矩阵表示为

(5)

3.3 路线合并问题模型的处理过程

本节将依据上述理论,给出路线合并问题模型的分析过程.

调度站点的全体即数据集U={u1,u2,…,um},调度站点间路线的全体即全体关联关系S={e1,e2,…,ek},根据政府的路线规划情况可得对路线(即关联关系)的划分E={E1,E2,…,En}.首先,依据关联组合结构的关联矩阵的定义,利用调度站点与路线间的关联关系情况得出以各路线为行,各调度站点为列的k×m矩阵M(P);其次,计算每一划分Ei(i=1,2,…,n)对应的行向量:若Ei={e1,e2,…,eη},各边对应行向量为(b11,b12,…,b1m),(b21,b22,…,b2m),…,(bη1,bη2,…,bηm),则划分Ei(i=1,2,…,n)对应的行向量为:((b11+b21+…+bη1)mod(η),(b12+b22+…+bη2)mod(η),…,(b1m+b2m+…+bηm)mod(η));之后,对全体Ei(i=1,2,…,n)的行向量组成的矩阵进行处理:删除列零向量及其对应的数据(即站点),合并列向量相等的数据点.最后,即得粒化结构的关联矩阵M(P)*,对M(P)*进行分析即可得到调度站点的调整情况以及调度中心的选择.

3.4 应用

为解决引言中所述模型问题,本节我们利用上述理论考虑公路路线的合并对调度站点设置的影响问题.在路线进行合并后如何调整调度站点,更好地实现对路线上各种问题的管理.并且依据分析,对调度中心的确立也能有较好地体现.

问题:将某城市的调度站点间公路路线集合记为S={e1,,e2,…,ek},调度站点的集合记为U={u1,u2,…,um},对于ei∩ej=uk∈U表示路线ei与ej有公共顶点(调度站点)uk,基于调度站uk可直接对路线ei与ej进行调度管理.例如:设施分配、应急救援等.关联组合结构表示了路线与站点间的关联关系.现在,在城市规划过程中,打算将部分路段进行合并,对于该规划,考虑调度站点如何进行调整.另外,调度中心为对各站点进行快捷供给的站点,那么,在路线合并后,考虑调度中心如何选择.

分析:基于上述理论可知,E为对关联关系S的划分,表示公路路线间的合并,那么对于粒化数据集U*来说,即为公交线路合并后调度站的更新重组情况.关联组合结构的关联矩阵可通过运算得到粒化结构的相关矩阵,数据集的粒化以及与关联关系划分之间的相关性可依据此矩阵看出.

解决:记该城市6个站点间的线路集合S={(1,2),(1,4),(3,4),(2,5),(2,6),(3,6)},U={1,2,3,4,5,6},其中U为6个调度站的集合,S为调度站间公路路线的集合,例如:(1,2)表示调度站点1与调度站点2之间存在路线,e1=(1,2),e2=(1,4),e3=(3,4),e4=(2,5),e5=(2,6),e6=(3,6).依据实际问题现将公路路线作以下划分,划分E={{e1,e2},{e3},{e4},{e5,e6}},其中{e1,e2}表示将路线e1与e2合并,{e5,e6}表示将路线e5与e6合并,其他路线不作变动.探究如何调整调度站点以适应线路的合并问题.

构造关联组合结构P=(S,U,E)的关联矩阵M(P),依据上述已知情况可得:

(6)

通过运算得粒化结构P*=(E,U*)的关联矩阵

(7)

分析:由粒化结构的关联矩阵可知,可将调度站1、6去掉,只利用2、3、4、5四个调度站即可实现对各路线的全面管理.并且,观察粒化结构的关联矩阵,可知站点2对应的列向量中包含的1数量最多,因此,与调度2号站关联的路线也最多.因此可将调度2号站作为调度中心.对路线、调度站点以及相应路线间的调整情况组成的关联组合结构的关联矩阵进行运算得到粒化结构的关联矩阵.因此,在今后的城市线路规划中,通过对此粒化结构的关联矩阵进行分析即可实现对调度站点调整和调度中心选择等问题的解决.