高维空间近邻检索的双层组合量化GPU加速算法

邓理睿，包 涵，陈 靓，全成斌，赵有健

1(清华大学 计算机科学与技术系，北京 100084) 2(中国石油勘探开发研究院，北京 100083)

1 引 言

高维空间中海量数据的高效检索问题，可以说是计算机视觉、信息检索等应用所面临的基本问题之一.主流的多媒体检索框架，都需要将音频、图像或文本等多媒体数据抽取一定特征，转化为高维向量，通过在高维空间中检索近似向量来查询所需的多媒体内容.

伴随互联网技术和多媒体技术的不断发展，网络空间内的各类数据呈现出爆炸增长的趋势.以社交网站Instagram为例，目前Instagram仅每日新增的分享图片数就接近1亿张，在线视频直播服务的兴起则更是产生了海量的音视频数据信息，对现有的图像、视频和文本内容分析技术的处理能力提出了更高的要求.随着数据规模的持续增长，结合数据本身存在的维度高、分布不确定等特点，如何对超过十亿规模、甚至更多的高维数据进行快速、有效地检索逐渐成为研究的重点和难点.

传统的树形结构检索、基于哈希的检索，在经过适当的改进后对于百万量级的高维特征库，如SIFT1M、GIST1M等，已经拥有较好的处理能力，但对于更高规模的数据，则往往只能借助大量服务器进行分布式处理[1].随着数据规模的不断提升，基于向量量化(Vector Quantization，VQ)的检索方法由于能够尽可能小的划分结果空间，在十亿量级的数据库上展现出了良好的性能，逐渐成为研究热点[2-6].尤其是如何尽可能提升计算密度，在单台计算服务器节点内进行高效检索仍然有待探索.

随着CPU的晶体管数增长速度放缓，GPU由于其SIMD模型具有计算密度高、可并行度高的特点，得到了长足发展.单张GPU的浮点运算性能目前已突破10Tflops，远远高出同等量级的CPU，在高性能计算中拥有广泛的运用.

为了充分挖掘GPU的并行运算潜力，本文基于组合量化(Composite Quantization，CQ)思想提出了一种针对GPU优化的大规模高维空间数据近似近邻检索算法，结合了组合量化算法与双层索引树结构，在建立次级量化码本时引入局部最优化思想，提高了量化精度，改善了在数据分布不规律时系统的检索性能.同时利用替代投影思想优化数据预处理过程，大幅度减少了显存占用，最终实现了高维空间海量数据的高效检索.

在拥有十亿条128维特征向量的SIFT1B测试集上，本文算法在单张GPU(NVIDIA TITAN Xp)上就取得了良好的检索效率：在与原组合量化算法的CPU版本检索精度基本不变(Recall@10=0.45，Recall@100=0.926)的情况下，平均单次检索仅需0.91ms，获得了超过50倍的加速比，性能提升显著.

2 相关研究

文献[1]总结了过去高维空间中近邻检索的相关算法，通常来说可以分为三大类：基于树型划分的方法、基于哈希的方法以及基于向量量化的检索方法.

早期的高维数据检索主要基于树形结构，例如K-D树、R树等经典算法，通过划分子空间逐层减小搜索状态，在空间维度相对比较低时(假设查询向量的维度K，数据量N，要求2K≪N)，拥有不错的查找效率；但一旦数据空间维度上升，由于算法本身的回溯特性，便会遭遇“维数灾难”，效率已经被证明甚至低于暴力枚举[7].

基于哈希的近邻检索算法核心思想是通过寻找合适的哈希方式将高维向量投影到低维空间，转化为低维空间中的相似性检索问题.其中的代表性算法如局部敏感哈希(Locality-Sensitive Hashing，LSH)[8]在百万量级的数据集上取得了很好的效率，目前已经在各类检索场景中被广泛使用[9，10].其主要缺点在于根据Johnson-Lindenstrauss定理，随着误差范围的减小，算法的空间复杂度将急剧上升.十亿量级的数据规模下LSH保持较高查询精度所需要的内存远远超出可承受的范围.

向量量化(Vector Quantization，VQ)是一种数据压缩方法.首先在目标空间中确定一组向量基，通常也称之为“码本”(codebook)，其中的每一个基称为一个“码字”，由于往往通过聚类求出向量基，因此码字通常对应一个聚类中心(centroid).通过将待处理向量近似转化为码本中码字的线性组合，实现数据的压缩，相应的组合系数也就是待处理向量量化后的编码.

在向量量化算法(表1)中，关键是码本的量化方法和数据索引存放的方法.在百万量级上进行检索，量化码本中只需要数千个码字(centroids)即可.然而随着数据量的不断提升，当面临十亿量级的数据时，为了取得较好的检索效果往往需要上百万个码字，仅仅逐一比较查询向量与码字的距离的代价就已经难以接受.

乘积量化(Product Quantization，PQ)算法[5]是Herve Jegou于2009年提出的一种具有里程碑意义的向量量化方法.假设原始向量属于D维空间RD，PQ算法将原始空间划分为M个M/D维子空间的笛卡尔积，分别在每个子空间内独立的进行向量量化，得到码本C1，C2，…，CM.若每个码本包含K个码字，则等价于在D维原始空间中拥有一个含有KM个码字的码本.对于数据集中的任一向量X，将其同样划分为M段，每一段在相应子空间内的码本上量化至最近的码字Ck(ik),k=1,2,…,M，故可以将其近似表达为：

x≈[C1(i1)，C2(i2)，…，CM(iM)]

(1)

对于查询向量q，其与数据集中任一向量X的距离可以表示为：

‖q-x‖2≈‖q-[C1(i1),C2(i2)，…，CM(iM)]‖2

(2)

其中qm表示查询向量在相应子空间内的分量.相应的，在查询时，原本需要与KM个维度为D的码字比较大幅降低为与M·K个维度为D/M的码字作比较，即复杂度由O(KM·D)降低为O(K·O).因此通过在预处理时建立合适的查找表可以极大改善检索效率.

PQ算法的改进.PQ算法在大规模数据集上表现出了突出的性能，受到乘积量化思想的启发，近年来相继提出了优化的乘积量化(Optimized Product Quantization，OPQ)[3]、局部优化的乘积量化(Locally Optimized Product Quantization，LOPQ)[4]等，通过旋转坐标系在全局或局部寻求最优划分，提升了算法的准确度.

表1 基于向量量化的算法总结Table 1 Summerize of vector quantization

由于PQ对空间的正交划分属于有损压缩，同样有许多研究试图针对这一问题做出改进：例如加法量化(Additive Quantization，AQ)[11]试图通过在原始空间多次量化，避免PQ算法中由于分段量化带来的信息损失；堆叠量化(Stacked Quantization)[6]则通过迭代量化残差的方式减小量化误差，但相应地带来了更大的计算开销.

Wieschollek等人进行了利用GPU加速乘积量化的尝试[12]，通过设立两级索引结构，减小了搜索空间，降低显存的访问次数；并且利用替代投影的预处理方式极大减少了数据量，通过良好的预处理，使得10亿条SIFT向量构建的索引库能被存放在一张GPU内.但由于乘积量化本身属于有损压缩，加上替代投影带来的信息损失，使得检索的准确度受到影响.

3 本文算法

本节将针对过往算法存在的问题，提出适应于GPU运算的基于双层索引结构的组合量化(Bilayer Composite Quantization，BCQ)的算法流程，并给出具体的说明.

3.1 算法流程与框架

基于向量量化的高维数据检索，都遵循共同的基本算法框架：

1)量化.通过算法指定的目标函数训练码本，并通过指定的量化方式，将待检索数据库中的向量一一量化至特定的码字上.

2)索引.将码字以一定的结构进行索引，方便快速查找，通常采用的是非对称倒排索引(IVFADC)或倒排多索引(Inverted Multi-Index)结构.

3)查询.对于待查询向量q，将其依照同样的步骤量化至一个特定的码字上，取出码字对应的索引列表，视为近似最近邻的候选列表.

4)重排序.将候选列表的原始向量取出，一一计算待查询向量q与其的原始距离，并根据距离排序，获得最终的近似最近邻列表.

下面我们将分步介绍BCQ算法的原理与流程.

3.2 组合量化的基本原理

组合量化(Composite Quantization，CQ)算法[13]是Wang Jingdong等人在PQ算法的基础上提出的一种新量化方式.

PQ算法存在的一个基本缺陷是，子空间的划分必须独立且相互正交，难以刻画更多数据分布.尽管诸如OPQ等算法通过旋转坐标系，能在一定程度上降低量化误差，但不能解决对于子空间划分的约束性过强的根本问题.

因此组合量化选择舍弃笛卡尔积，采用更直观的方式将向量近似量化为一组向量基的加和：

x≈C1(i1)+C2(i2)+…+CM(iM)

(3)

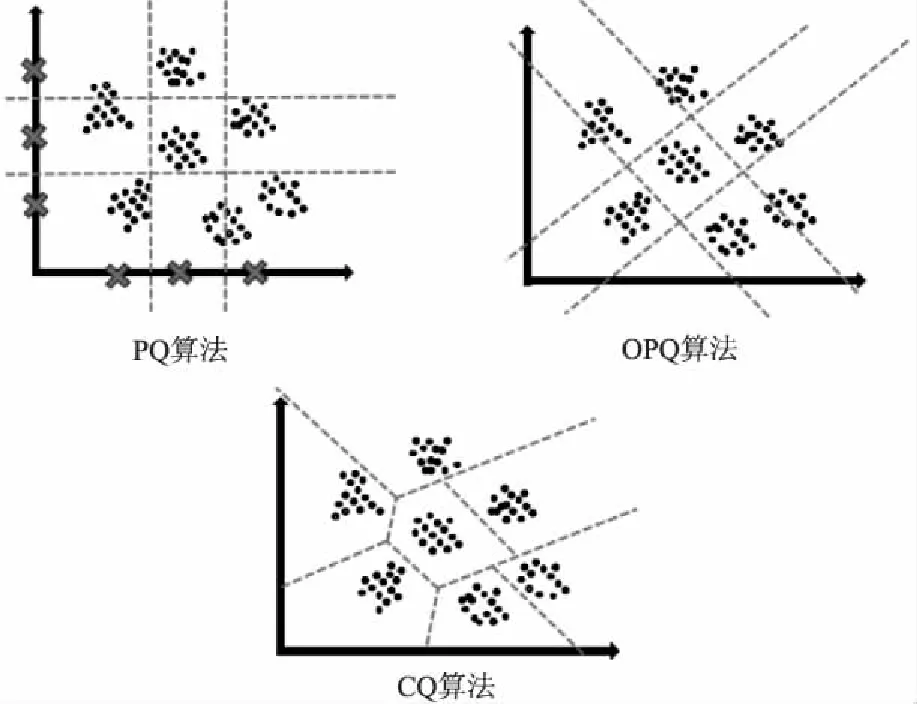
图1 不同量化算法的空间划分Fig.1 Space partition of different quantization

图1所示为不同量化算法对空间的分割情况.由图中可以看出，与PQ单纯将空间正交划分相比，通过将向量以加和的方式解析，CQ算法能够在码本大小相同的情况下，更好的拟合数据本身的分布情况，减少错误划分的数据点.

根据式(3)采用的量化方式，求查询向量q与数据集中任一向量X的距离可以表示为：

(4)

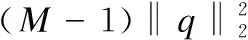
(5)

然后通过轮流最优化迭代求解.

3.3 双层索引与局部最优化

然而原始的组合量化算法同样仍面临一些未解决的问题，例如：

1)检索时间的线性增长.随着数据规模增长，子空间划分数M和每个子空间内的码本所需的码字数K都需要相应增长，否则带来的后果就是倒排索下，每个编码index对应的向量数线性增长.而所有的量化方法，在将查询向量量化后的重排序过程都需要线性扫描对应编码Index下索引的所有向量，并一一计算实际距离.在CQ算法的原始论文测试数据中也表明，在10亿向量的SIFT 1B数据库中进行单次检索所需的平均时间超过了在100万向量的SIFT 1M数据库中进行检索的100倍以上，需要秒级检索时间.

2)空间分布的非均一性.尽管CQ相较于PQ与OPQ而言，拥有更灵活的空间分割方法.然而事实上在个子空间中，数据的分布性质又可能各有不同.

为了解决这一问题，本文算法采用双层索引树结构拓展了原有的组合量化算法.

在索引树首层采用向量量化，不妨设码本中的码字数量为ω；在每个码字(Centroid)所划分的Voronoi子空间内，同样的我们考虑局部子空间内的分布最优化，再次进行组合量化，得到M个量化码本，大小为K.假设单层索引量化需要将量化粒度控制在同样粗细，则需要总空间划分数ω·KM.由于在检索时需要对最终候选列表进行重排序，因此码本扩大ω倍即检索空间缩小ω倍，即量化时间由O(K·M)增长为O(ω+K·M)，但重排序时间由O(T)缩减至O(T/ω).

由于通常情况下

(6)

因此取

(7)

时，可以获得接近ω倍的加速比.

同时，由于建立双层索引结构，在二级子索引时，可以分别在每个子空间内采取局部最优化策略.LOPQ算法正是利用这一策略取得了比OPQ算法更高的准确率[4].

与传统PQ算法一样，为了确保在子空间切分后，不会遗漏有效候选向量，我们在此处还采用“多分配策略”[5]，在索引树的多个分支中同时查找(见图2).实践表明多分配策略在量化检索中能有效的提高召回率.

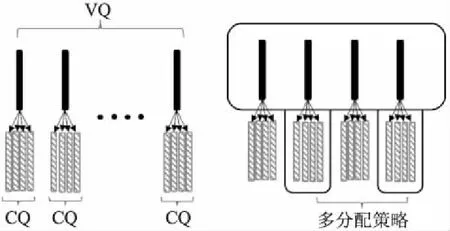
图2 双层组合量化与多分配策略Fig.2 Bilayer Composite quantization and multi assign strategy

3.4 替代投影与重排序

除了数据分布不均一外，量化查询另一信息损失过程在于查询向量到量化中心的距离，并不直接等于查询向量到候选向量的距离.传统的量化检索算法在完成对向量的量化、索引树的建立后，在最终查询时需要将完整的向量库读入内存，以便在获取量化编码后，能迅速获取对应量化编码的倒排索引列表中的所有候选向量的原始值，然后计算查询向量与候选向量的实际距离，并完成重排序.

假设倒排索引中每个候选列表的平均长度为L，

(8)

则重排序所需的复杂度为O(L·D·m)，其中m为多分配系数，D为向量维数；而空间复杂度为O(N·D).

以SIFT 1B为例，10亿条128维浮点数向量，N=1010，D=128×4 bytes，其所需内存为92GB，而通常GPU的显存在10G左右，无法在单张GPU内完成运算.因此我们还需要基于GPU的架构优化最终的检索与重排序流程.

一个直观的想法是，通过尽可能的预处理，减少所需存储的数据维数.传统的量化在寻找到向量的最近码字后，是以查询向量到码字的距离近似实际距离，Wieschollek提出可以用向量的投影点作为替代：

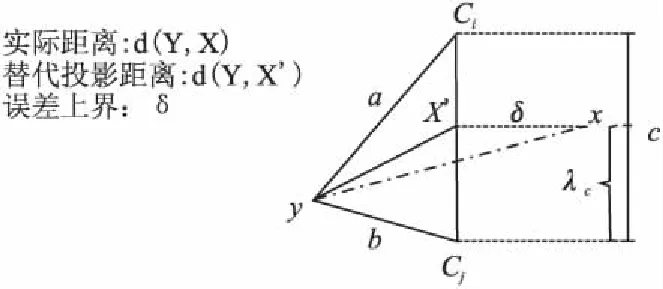
图3 替代投影示意图Fig.3 Substitute Project

如图3所示，需要计算y到x距离，以下记为d(y,x).传统上，我们在量化时以y到最近的码字(不妨设为Cj)的距离d(y,Cj)代替d(y,x)，根据三角关系其误差上界为d(Cj,x).

如果将x投影至最近的两个码字连接成的直线上得到x′，采用用d(y,x′)代替d(y,x)，由Δyxx′三边关系可知其误差上界为δ，且δ必定小于d(Cj,x).即：

d(y,x)≈d(y,x′)=b2+λ2·c2+λ(a2-b2-c2)

由于a，b，c均与查询向量无关，可以在预处理时确定，故对于每个数据点x，无论其原始维度为多少，仅需保存相应的码字编号i、j，及其投影到码字连线上的点的位置偏移λ.空间复杂度骤降至O(N·M)，M为量化子空间划分数.此时处理SIFT 1B所需显存已经降低至5G，可以在单张GPU上实现.

4 实验及数据分析

基于上一章中给出的优化后的双层索引组合量化算法，本章对相应检索系统进行了实现.通过对算法检索准确率、运行效率的测试，以及与其他相关研究的对比，分析了算法的性能.

4.1 实验环境

硬件环境：

CPU：Intel Xeon E5-2620V4 @ 2.2GHz，8核16线程

RAM：128G DDR4 2400

GPU：NVIDIA TITAN Xp，12G显存，3072个CUDA核心

测试数据集(表2)：

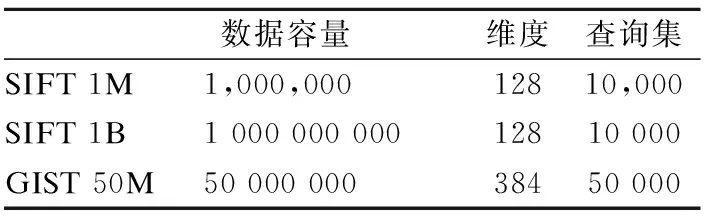
表2 测试数据集Table 2 Test Dataset

包括标准的公开数据集SIFT 1、SIFT 1B，分别含有100万条与10亿条128维SIFT特征向量，以及包含有5000万条384维GIST特征向量的GIST 50M数据集.

4.2 实验结果及分析

本节实现了上文描述的双层索引组合量化算法(以下简称BCQ)，并在数据集上测试后，与过往的CPU量化算法如OPQ、CQ以及GPU量化算法PQT进行对比分析.

为了确保测试数据的可比较性与对比的公平性，与各算法的对比测试均保持量化编码长度为128bits，重排序候选链表长度为10000，并计算10000次查询的平均检索时间.

1)算法性能测试

表3 SIFT 1M数据集测试结果Table 3 Performance on SIFT 1M

从表3中可以看出：对于SIFT 1M数据集，目前的主流算法均取得了较高的召回率.检索速度也远远超出诸如视频图像的实时检索(30 frame/s，即33.3ms/query)等应用的需求.说明百万数量级的、较低维度的特征检索对主流的量化检索算法已经不构成挑战.

表4 GIST 50M数据集测试结果Table 4 Performance on GIST 50M

从表4中可以看出，随着特征维度的升高，各类量化检索方法的准确度都有所下降，且PQT算法的降幅十分明显，其检索精度已经基本不具有可用性.此时BCQ算法的精度仍然较为良好，达到甚至超出了CPU算法的准确率.

综合表4表5不难发现，随着数据量的迅速增长，数据点在高维空间中的分布逐渐稠密，局部子空间最优化的量化方法由于对空间结构的更优分割，在检索准确度上的优势便越发明显.

表5 SIFT 1B数据集测试结果Table 5 Performance on SIFT 1B

上文已经提到，目前互联网空间中每日新增的多媒体数据都是以数亿量级增长，因此当我们将目光聚焦在十亿及以上量级中的高维数据检索时，原有的CQ算法尽管准确率高，但运行时间过长，在SIFT 1B中单次检索需要242.3 ms，远远不能满足各类多媒体检索实时应用(即>30 frame/s)的需求；PQT算法尽管检索速度取得了飞跃，但召回率往往不足80%甚至更低，难以达到实际应用的要求.

而基于GPU实现的BCQ算法由于充分挖掘了GPU的并行计算能力，即使在10亿量级的数据库上仍然取得了平均单次检索时间0.91ms的极高效率，相较于CPU算法有了大幅度的提高，与OPQ算法相比也有50倍左右的加速比，足以应对各类多媒体信息处理系统中的实时要求；同时相较于现有的GPU算法，在运算速度相近的条件下，召回率大幅提高，近似保持了CPU算法的准确度，使得算法在真实应用场景下具有更好的可用性.

2)算法稳定性测试

相应的，我们还测试了BCQ算法在不同编码长度下的表现.编码长度越短，所需要的计算时间越短，但相应的检索精度也有所下降.

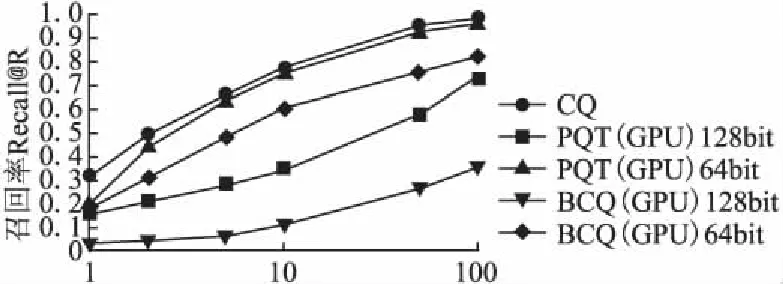
图4 在SIFT 1B数据集上的召回率曲线Fig.4 Recall curve on SIFT 1B

从图4中我们可以看出，相较于同样是基于GPU的PQT算法，BCQ算法从128bit编码到64bit编码的召回率降幅明显更小；且即使在64bit编码下，BCQ(64bit)的检索精度依然高于PQT(128bit)，可见算法的鲁棒性十分良好.

5 结 论

本文提出了一种基于GPU优化的高维空间组合量化高效检索算法.针对过往算法运行速度较低的问题，在组合量化的基础上，通过引入双层索引结构及投影量化方法，大幅提高了检索效率，在单张GPU上对10亿量级的高维数据实现了检索速度超过1000fps(单次检索0.91ms)、召回率为92.6%的高效率、高精度检索.在保持原有CPU算法经度的情况下获得了超过50倍的加速比；较已有的GPU算法在运算速度相近的情况下提升了20%的召回率，达到了0.926，大大改善了原有算法的可用性，为互联网空间海量多媒体数据的各类应用打下了良好的基础.