一种多级全固体运载火箭上升段自主制导方法
2019-02-15李新国
张 迁,许 志,李新国
(1. 西北工业大学航天学院,西安 710072;2. 陕西省空天飞行器设计技术重点实验室,西安 710072)
0 引 言
近年来小卫星由传统的搭载开始向商业购买发射服务转变,呈现个性化、定制化、众筹化的特点,而小型固体运载火箭凭借快速机动发射、可靠性高、成本低等特点业已成为发射任务的首要选择。2013年“Epsilon”火箭的成功发射,在快速响应航天运载器领域产生了很大震动,其标准型采用了三级全固体火箭方案[1]。由于免去了液体火箭在临射前加注燃料等流程,最短发射准备时间缩短至24 h以内,在自然灾害、突发事件的应急发射任务中具有显著优势,同时在商业航天领域同样有着强大的竞争力[2]。然而,相对于液体火箭发动机,固体火箭为了提高质量比及可靠性取消了推力终止机构,导致只能采取燃料耗尽关机而不能进行制导关机;此外,固体发动机具有工作时间短、推力大等特点,必须采用“助推-滑行-助推”飞行模式才能保证对不同发射任务的适应性。上述特点给全固体火箭的制导技术带来了新的困难与挑战。
国内外学者针对上升段制导算法的研究主要集中在液体运载火箭的最优闭环制导问题。Brown等[3]针对大气层外飞行器的在线制导给出了线性模型最优解析解。在此基础上,文献[4]设计了一种迭代制导算法在线迭代求解最优解析解的待定参数;文献[5]对闭环最优制导进行梳理,总结了多种任务约束下迭代制导方法的最新研究成果。文献[6-8]等根据变分法最优控制原理推导了燃料最省的上升段轨迹最优解,并分别采用了多重打靶法、有限差分法、配点法等数值算法进行求解。文献[9-10]开展了固体火箭上升段弹道快速设计方法研究,设计了基于Gauss伪谱法的轨迹优化策略使轨迹优化效率进一步提高。对于液体火箭或具有液体上面级的固体火箭,上述算法能够在满足终端约束的同时保证飞行轨迹的最优性;然而,针对耗尽关机的全固体运载火箭,必须考虑剩余能量管控与发动机大散差抑制等问题,这与以燃料最省的液体运载火箭制导方法有显著的差别。因此,在快速响应需求下全固体运载火箭制导必须解决具有固定总冲约束的两点边值问题。
而固体火箭制导算法的研究主要是对经典的闭路制导[11-13]进行改进。针对闭路制导鲁棒性问题,文献[11]考虑发动机性能参数散布特性,提出需用速度增益曲面的概念并设计了基于该概念的大气层外导引方法。针对以轨道根数为终端约束的制导问题,文献[12]根据实时飞行状态与轨道根数之间的关系推导出需要速度求解方程,并应用于发射近圆轨道的闭路制导控制中。文献[13]考虑了地球非球形J2摄动项对弹道的影响,改进了需要速度求解算法以修正地球引力摄动在长时段飞行过程中引起的求解偏差。由于未考虑耗尽关机方式下火箭的速度管控问题,上述闭路制导算法无法直接应用于具有轨道能量约束的太阳同步轨道(SSO)发射任务。针对耗尽关机能量管理问题,文献[14-16]等通过设计不同的能量管理曲线来实现对耗尽关机速度矢量的管控。但是,上述算法由于以需要速度矢量为导引量而忽略了制导过程中位置矢量变化对终端约束产生的影响,故针对终端多约束条件的入轨任务其制导精度较差,鲁棒性无法保证。
为满足终端多轨道根数约束,文献[17-20]根据轨道动量矩守恒定律推导出具有速度矢量及位置矢量约束的定点制导算法。本文在PA[20]制导算法的基础上设计了一种适应于多子级“助推-滑行-助推”模式的制导算法,通过具有轨道能量约束的滑行过渡轨道将多级推进段制导统一起来,根据当前飞行状态与终端轨道根数约束推导出满足发动机耗尽关机条件的过渡轨道求解方程,进而确定出轨道根数约束与火箭点火时间及推力矢量方向的数学关系。
1 固体火箭上升段制导问题
1.1 质心运动模型
在发射惯性坐标系下运载火箭质心运动方程[20]表示为:
(1)
T为发动机推力,轴向和法向气动力分别为A和N,其表达式为:
A=qSCA,N=qSCN
xb和yb分别表示弹体轴向和法向。固体运载火箭发动机的推力大小与秒流量不可调节,式(1)中实际上需要确定出弹体方向xb的控制指令,使运载火箭以耗尽关机的方式满足入轨约束条件。当运载火箭进入真空环境,大气压强P(h)产生的推力及火箭所受的气动力予以忽略,运载火箭所受的气动载荷及气动角等过程约束也随之消失,为自主制导算法的设计提供了更大的空间。由于大气层内飞行轨迹的偏差可以通过大气层外自主制导算法进行修正,本文重点研究大气层外多约束自主制导算法。
1.2 实际推力非线性问题
固体发动机能够提供的视速度模量WM随推进剂质量ms变化的表达式为:
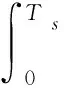
(2)
在耗尽关机模式下,当推进剂质量ms确定则视速度模量WM为常值。视位置模量RM随推进剂质量ms变化的表达式为:
(3)
发动机持续推进过程的形心时间Tc表达式为:
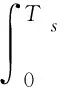
(4)
然而,发动机在燃烧过程中由于外界压强、温度等环境因素以及燃烧过程化学反应程度的影响,实际性能参数与工况条件下相比偏差较大,非线性程度较液体发动机更为明显,如图1所示。
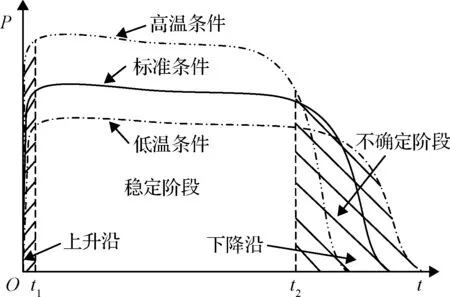
图1 固体发动机性能参数曲线在高低温条件下散布示意图Fig.1 Profile of the performance distribution with solid motor thrust-time diagrammatic drawing
当发动机装药量ms一定时,图1中不同条件下曲线所围的面积是相同的,式(2)依然成立,即视速度模量为常值,但视位置模量随着秒流量的散布而产生偏差。由于火箭在实际飞行过程中发动机真实燃烧曲线无法提前获知,发动机模型的不确定性及非线性使制导律的设计更为困难,最优化制导算法通常未考虑实际非线性推力散布模型或者认为发动机的模型提前已知,因此无法直接应用于实际工程问题。针对上述发动机特性,要求制导律在满足约束条件下尽可能减小姿态角变化率以增加终端制导精度。
1.3 耗尽关机多约束问题
运载火箭的终端约束为卫星载荷的轨道要素,通常轨道根数约束为半长轴a、偏心率矢量e及轨道倾角i等,表达式如下:
(5)
固体运载火箭入轨任务约束为轨道要素方程式(5),由于终端轨道根数约束条件的不同,运载火箭受到约束的状态量也随之改变。此外,由于固体火箭发动机以燃料耗尽的方式关机,推进段发动机产生的总速度增量和总位置增量为定值,满足式(2)及式(3)约束。
固体运载火箭由于在大气层外通常采取“助推-滑行-助推”飞行模式,即在滑行阶段确定发动机点火时间,在推进阶段确定制导指令,使式(1)满足终端约束。因此,针对全固体运载火箭,制导算法本质上是求解具有固定总冲约束的两点边值问题,而其算法的核心则是:
(1) 推导出推力矢量、点火时间与终端状态约束之间的理论关系;
(2) 确定能量匹配的滑行过渡轨道以保证推进段耗尽关机约束要求。
2 PA制导算法
2.1 PA理论基础
固体火箭发动机推力脉冲大,工作时间短,可以快速产生瞬时速度冲量,此时火箭弹体方向沿着速度冲量方向[11-13]。实际上,发动机需要经过额定工作时间才能完全耗尽产生相应的速度冲量,PA制导算法主要研究“瞬时脉冲矢量”与“定向持续推力矢量”在实现入轨任务时的理论关系[17-20]。因此,假设发动机持续推进过程中推力矢量方向始终沿着速度冲量方向Γ。详细理论推导过程参考文献[20]。
当运载火箭在真空环境中以定向的推力矢量方向飞行,其动力学方程为:
(6)
式中,由引力产生的状态分量表达式为:
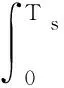
式(6)所描述的运载火箭运动方程可分解为:沿原来的开普勒轨道继续滑行及沿定向推力的作用产生位移矢量和速度矢量,表达式如下:
(7)
那么,持续推力过程引起运载火箭动量矩的变化为:
ΔH=mfrorb, f×vorb, f-m0r0×v0
(8)
将式(7)代入式(8)得到:
ΔH=mf(rsub, f×vsub, f+rsub, f×WMΓ+
RMΓ×vsub, f+RMΓ×WMΓ)-m0r0×v0
(9)
化简式(9)并整理得:
ΔH=mfrsub, f×vsub, f-m0r0×v0+
mf[rsub, f-(RM/WM)vsub, f]×(WMΓ)
(10)
在过渡轨道面和目标轨道面确定出轨道面交线Rimp,轨道相关参数的矢量关系如图2所示。
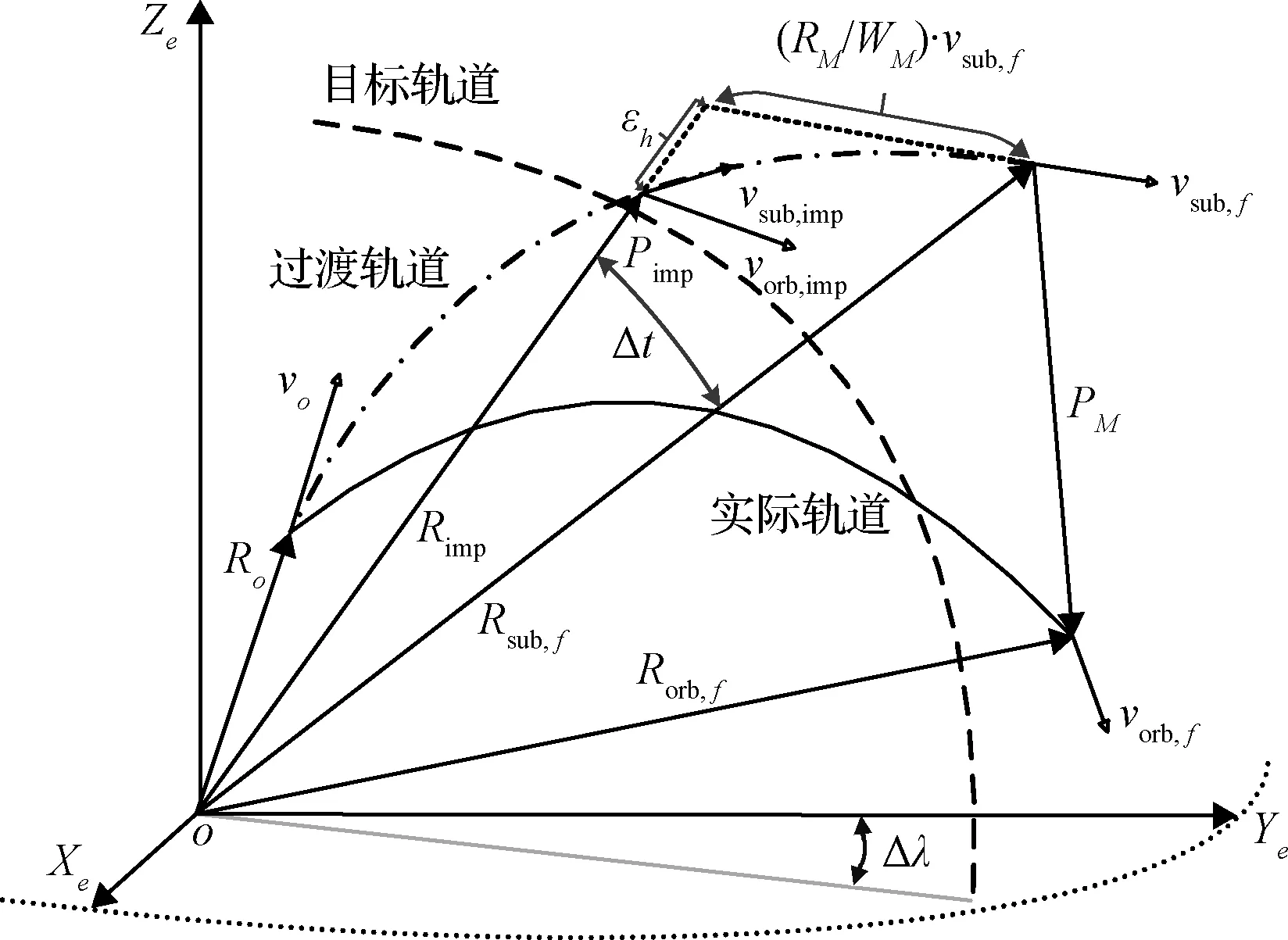
图2 PA制导算法运动分解图Fig.2 Motion analysis of pointing guidance method
令等效位置矢量rimp为:
rimp=rsub, f-(RM/WM)vsub, f
(11)
将式(11)代入式(10)得:
ΔH=mfrimp×(vsub,imp+WMΓ)-m0rimp×vimp
(12)
式(12)表明:“定向持续推进过程”对轨迹的改变与在等效脉冲点Pimp处施加“瞬时脉冲矢量”对轨迹的影响等效。
2.2 PA制导指令解算
运载火箭的状态矢量(r,v) 通常建立在地面发射坐标系,通过地心惯性赤道坐标系与发射系之间的变换矩阵得到火箭的惯性状态矢量,从而得到相应的轨道根数。在轨道面交点Pimp处,速度矢量关系如图3所示,通过滑行轨道参数求得:
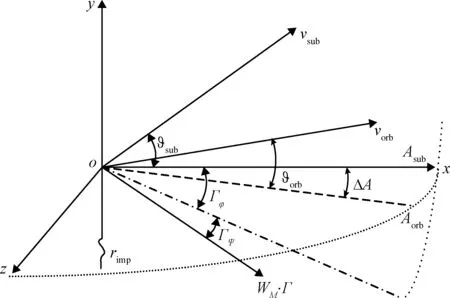
图3 轨道交点处速度矢量关系Fig.3 Vector diagram of the orbit intersection point
(13)
同样地,根据目标轨道参数得到:
(14)
根据式(13)和式(14),求解出轨道面交点Pimp处的真近点角、切向速度及法向速度。同时根据轨道倾角i和Pimp的经度、纬度,求解出速度矢量的方位角Asub和Aorb。因此,在两轨道交点Pimp处速度矢量表示如下:
(15)
进而得到PA制导所需的速度矢量大小和方向:
(16)
轨道面交点Pimp根据终端轨道根数约束而求得,则火箭从当前点飞行至交点Pimp处的时间为:
(17)
timp-sub, f=timp+RM/WM
(18)
根据式(4)、式(17)和式(18)得运载火箭点火时间为:
ta-ig=ta-imp-Tc
(19)
综上所述,以定向推力矢量的方式进行制导时,终端轨道位置矢量约束通过滑行轨道的点火时间式(19)来满足,速度矢量约束通过发动机定向推力矢量式(16)来满足,从而满足终端多轨道根数约束。
3 多子级改进PA算法
3.1 PA理论拓展
对于耗尽关机的固体运载火箭,由于无法制导关机,火箭对速度、位置的管控能力受限。为满足终端多轨道要素约束条件,单子级火箭采取附加姿态机动的方式耗散多余能量,导致姿态角速率变化剧烈;多子级火箭可以通过“助推-滑行-助推”的模式,使火箭的动能与势能转换,通过最佳的滑行轨道来匹配各级火箭发动机的总冲量,能量管控的实现机理如图4所示。
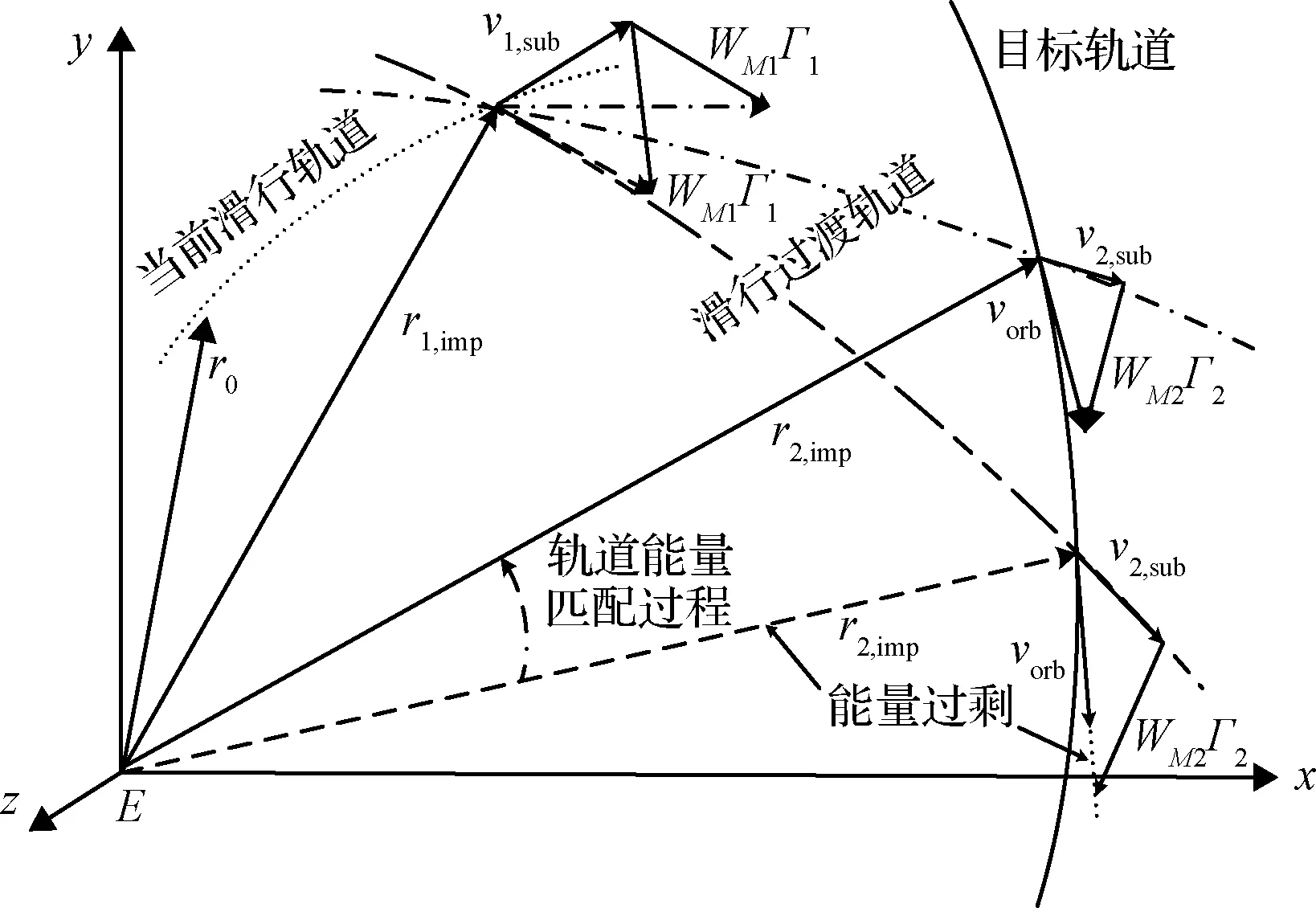
图4 多子级改进PA算法能(MPA)量匹配过程示意图Fig.4 Profiles of the energy matching process by the MPA
在式(12)基础上,多子级火箭持续推力过程引起的轨道动量矩变化为:
ΔH=mnrn×vn-…-m1r1×v1-m0r0×v0
(20)
根据PA理论,将式(12)代入式(20)得:
ΔH=mnrn,imp×(vn,imp+WM,nΓn)-…-
m1r1,imp×(v1,imp+WM,1Γ1)-m0r1,imp×v1,imp
(21)
各级火箭发动机推进过程中动量矩的变化通过脉冲点ri,imp(i∈[1,n]) 联系起来。为满足耗尽关机条件,由式(21)、式(16)及式(2)得:
Wi,PA=WM,i,i=1,2,…,n
(22)
根据终端轨道根数约束式(5),通过改变定向推力矢量方向Γi(i∈[1,n])来达到耗尽关机终端多约束条件。火箭各阶段的点火时间根据式(17)得:
(23)
3.2 改进算法降阶求解
以PA理论为基础,滑行过渡轨道将多子级耗尽关机问题统一起来,根据滑行轨道参数解算推力矢量方向Γ。以四子级全固体运载火箭发射SSO轨道为例,求解最佳能量匹配滑行轨道参数。
根据终端轨道根数条件及SSO轨道偏心率eorb为零得:
(24)
根据开普勒轨道的性质,火箭处于滑行轨道阶段,轨道动量矩和轨道能量守恒,因此当前轨道参数与运载火箭状态量满足:
(25)
同样地,滑行过渡轨道参数与运载火箭状态量满足:
(26)
其中,v0⊥,v1,orb⊥,v2,sub⊥分别表示在点P0,P1,imp,P2,imp处的径向速度分量。在轨道交点Pi,imp处速度矢量方向如图3所示,相应的表达式为:
(27)
由于轨道倾角的调整发生在P1,imp处完成,火箭的后续飞行将处于轨道面内,将终端约束式(24)代入式(26),并根据矢量方向关系式(27)得:
(28)
同样地,将滑行过渡轨道约束式(28)代入式(25),并根据矢量关系式(27)得:
(29)
根据运载火箭导航解算的状态向量(r,v) 及等式方程组式(25)、式(26)、式(28)和式(29),解算满足耗尽关机多约束条件下的推力矢量方向Γ。上述方程组为超越方程无法直接获得解析解,为保证算法的有效性,以v1,orb为迭代变量,将非线性方程组的求解问题转化为一维求根问题,具体流程如下:
(1) 确定迭代变量v1,orb区间[v1,sub,v1,sub+WM,1]:由于火箭处于上升段有v1,orb≥v1,sub,根据速度矢量得v1,orb≥v1,sub+WM,1。
(2) 解算推力矢量方向Γ2,从而得到切向速度v2,sub⊥;根据轨道能量方程式(26)和约束式(28),得:
(30)

(31)
因此,更新后的速度为:
cos(ϑ1,sub-Γ1,φ)
(32)
(5) 根据v1,orb和v2,sub⊥解算最佳能量匹配滑行轨道参数:
(33)
运载火箭在实际飞行过程中,由于受到干扰及不确定性的影响或发生非灾难性故障导致原定飞行任务无法现实。在这种特殊情况下,运载火箭由于后续运载能力的不足,使原方程的收敛解处于流程(1)的迭代区间之外,导致迭代算法失效。针对上述问题,制导算法需要根据当前运载火箭的飞行条件在线调整飞行任务约束以保证火箭的飞行安全,飞行任务的终端轨道根数调整过程如图5所示。
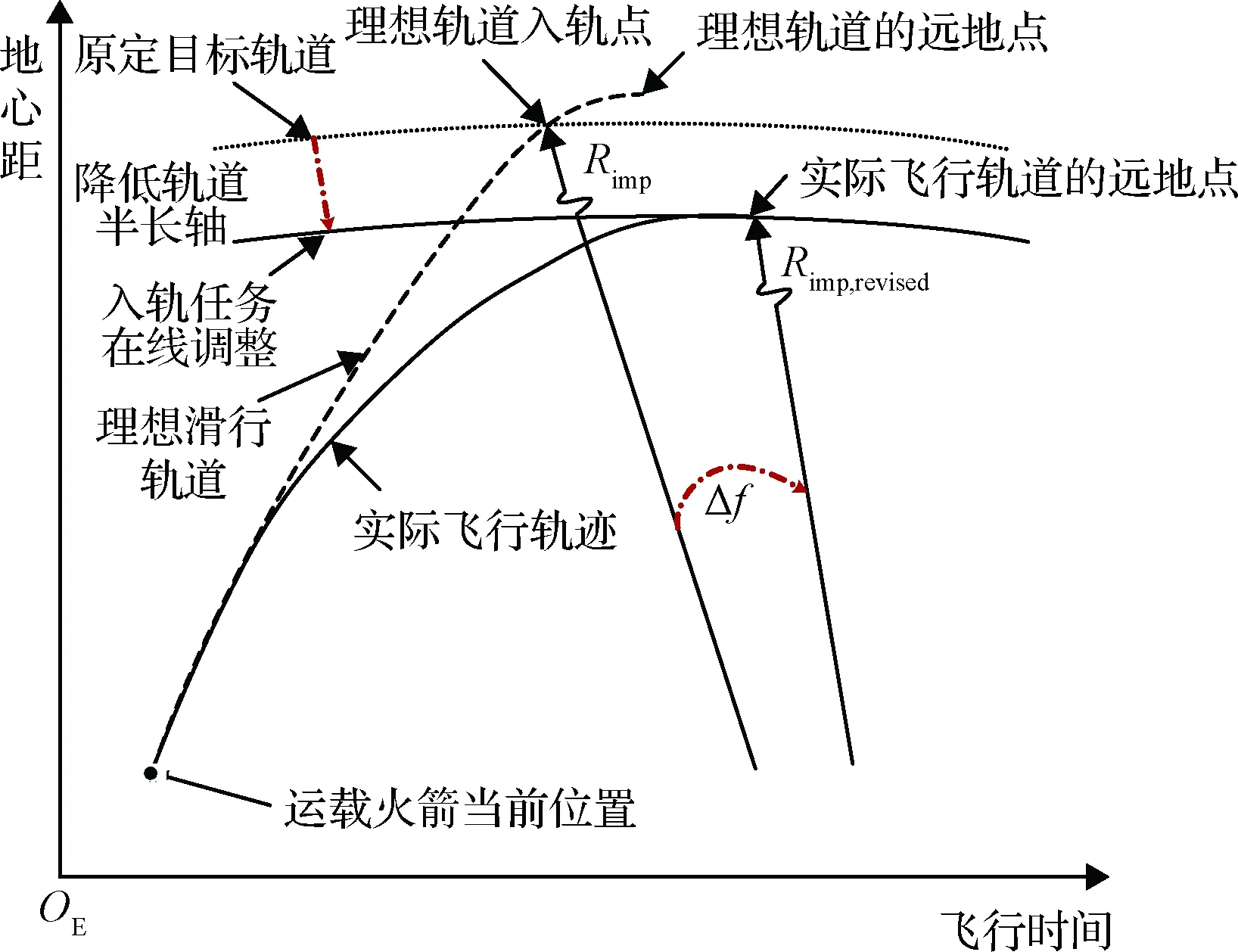
图5 飞行任务调整示意图Fig.5 The adjustment process of trajectory geometry
根据轨道根数表达式(5)可知,轨道半长轴是轨道能量的函数,因此,通过降低轨道半长轴使原方程的收敛解处于流程(a)的迭代区间内,以保证运载火箭尽可能地实现原定飞行任务。对于一维求根问题,当方程的解在迭代区间内时,黄金分割法在迭代10~20步以内可获得高精度解,根据式(33)计算满足能量约束的滑行过渡轨道参数,然后根据式(16)解算导航坐标系内的制导指令,并根据式(19)计算火箭点火时间。随着火箭持续飞行,多级问题将转换为单级问题,根据式(16)和式(19)在线解算制导指令,直至火箭进入目标轨道。
4 仿真校验与性能评估
飞行任务以太阳同步轨道(SSO)为例,考虑地球自旋角速度及引力J2项摄动。本文研究对象采用四子级全固体运载火箭,其制导算法流程如图6所示,制导方案如下所述。
1) 大气层内采用开环方案飞行,二级耗尽关机后,运载火箭位于大气层外飞行轨迹的偏差以导航输入的方式提供给自主制导算法。
2) 运载火箭第三子级采用多级改进PA算法,在线解算出最佳能量匹配轨道,通过调整滑行过渡轨道的能量与动量矩,使发动机总能量与飞行任务相匹配,以弥补发动机采用耗尽关机时运载火箭对速度矢量管控的不足。
3) 由于第三子级已经考虑了发动机多余能量的消耗问题,运载火箭第四子级只需通过PA制导算法确定实际点火时间及推力矢量方向,即可使运载火箭以耗尽关机的方式进入目标轨道。
4) 第四子级耗尽关机时,火箭基本满足入轨参数约束,末修级由于燃料的限制,主要小幅度修正速度偏差。
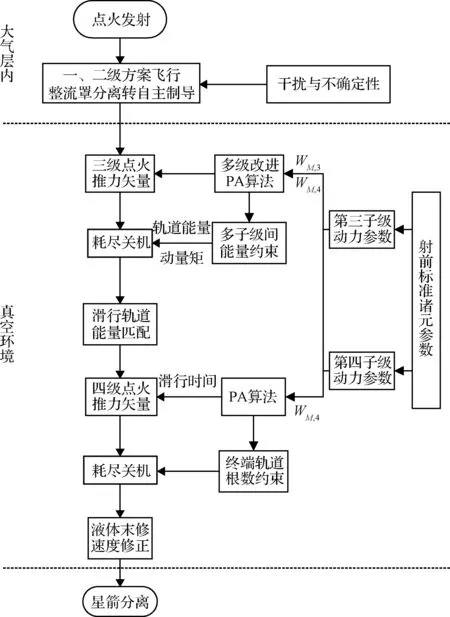
图6 制导方案流程图Fig.6 Flow chart of the guidance scheme
制导算法所需要的诸元参数按标称值预先装订,在仿真模型中偏差散布及不确定性对飞行轨迹的影响以导航输入的方式供制导算法在线解算制导指令,各项随机偏差由每次打靶随机产生,且服从正态分布,其中发动机模型采用实际内弹道推力曲线,并通过高低温的形式表征发动机性能散差,模型不确定性及散差分布见表1。
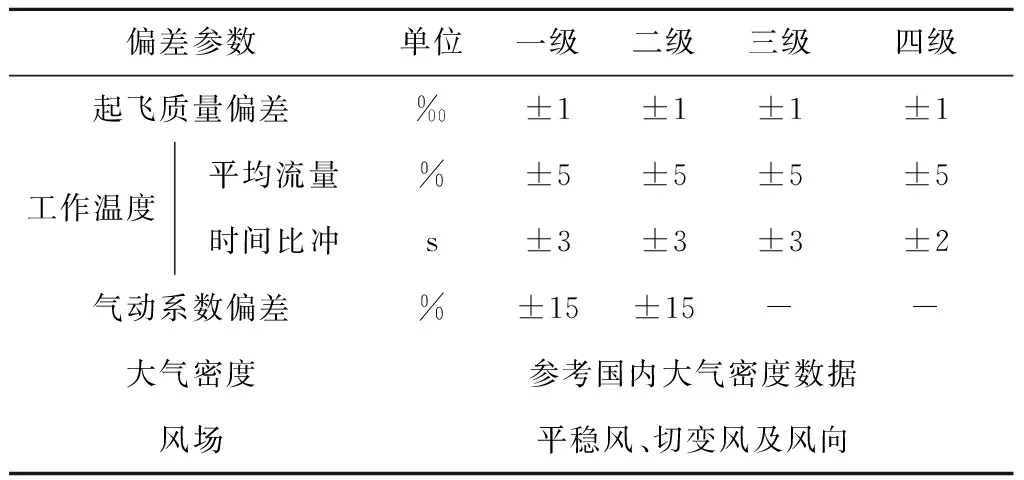
表1 蒙特卡洛仿真散差配置表Table 1 Dispersions in Monte Carlo simulations
4.1 多轨道任务自适应性分析
为验证制导算法对发射任务的适应性,考虑700 km SSO轨道最大载荷、空载荷两种典型情况,并以最大载荷方案设置终端轨道高度为300 km、700 km两种常用卫星轨道,终端状态约束见表2。根据所设置的三种典型发射任务条件,各方案分别进行1000次蒙特卡洛仿真,其散差配置见表1。其中,火箭轨道地心距变量以终端地心距约束值进行单位化,绝对速度变量以终端入轨速度约束值进行单位化,三种发射任务条件下的蒙特卡洛仿真曲线簇绘制结果如图7所示。
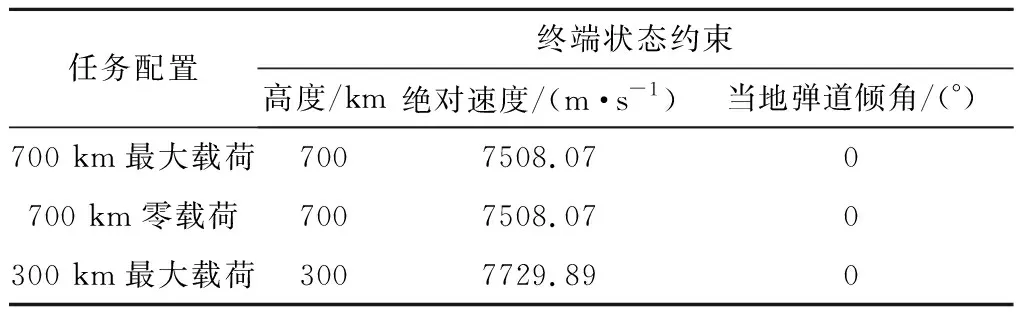
表2 运载火箭发射任务配置表Table 2 Missions and terminal state constraints in Monte Carlo
图7(b)绝对速度变化曲线簇中出现飞行过程绝对速度超过目标速度的情况,因为300 km满载与700 km空载分别对应轨道高度的变化与有效载荷质量的改变,使运载火箭均存在发动机能量过剩的情况,通过在线自主制导算法使状态量均达到目标值,表明制导算法对不同任务的适应性,且针对固体火箭发动机不同程度的能量过剩情况均能达到耗尽关机条件。
图7(a)~图7(d)中各状态量曲线随时间推移均达到目标值,表明了制导算法的终端约束能力;
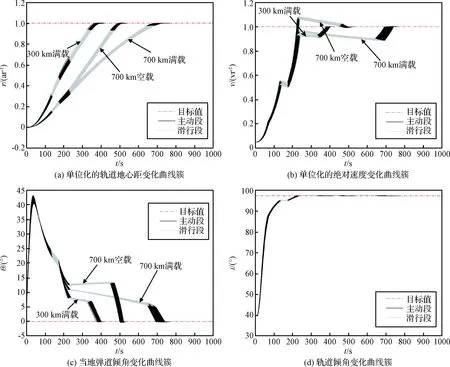
图7 蒙特卡洛仿真状态矢量曲线簇Fig.7 Profiles of the states run for Monte Carlo simulation
虽然偏差干扰源使运载火箭飞行轨迹改变,但应用在线自主制导算法后状态量通过不同的曲线形式均达到目标值,表明了制导算法对终端状态的高精度约束能力,其中曲线簇的宽度代表了制导算法对各干扰源的鲁棒性。
4.2 制导精度与鲁棒性分析
运载火箭以轨道根数为终端约束条件,飞行状态矢量(r,v) 与轨道根数满足相互对应关系式,但不同的轨道根数对状态矢量的敏感度不同。轨道半长轴受速度大小的影响比较明显,轨道偏心率与轨道倾角对速度矢量方向更为敏感。第4.1节仿真结果校验了PA制导算法对终端状态的约束能力,而针对多子级间轨道能量匹配与耗尽关机问题,通过运载火箭飞行过程中轨道能量与动量矩的变化,来验证多级PA改进算法的自主性、制导精度及鲁棒性。轨道能量与动量矩的变化如图8所示。

图8 多级PA自主能量匹配仿真曲线簇Fig.8 Profiles of the energy matching process by the multistage pointing algorithm
针对不同的发射任务,通过多级PA改进算法在线解算滑行过渡轨道根数约束条件,使发动机产生的速度矢量增量与实现轨道任务所需的速度矢量相匹配,来满足固体火箭耗尽关机条件。在不同初始条件下图8(a)轨道能量变化和图8(b)动量矩变化均达到终端约束值,展现出制导算法的自主性,同时也体现出算法对不同干扰的鲁棒性。
由图9可知,终端偏差比较集中且散布较小,但依然存在野点,半长轴偏差的最大值为1520.9 m,轨道倾角偏差的最大值为1.4×10-2(°)。主要原因为:一方面,大气层内未加横法向导引的开环飞行,受气动及风干扰影响导致飞行轨迹偏差较大;另一方面,发动机性能参数的偏差既不能提前获知也无法在线测量,导致耗尽关机点必然存在状态偏差。
3000次蒙特卡洛仿真的终端轨道要素偏差的统计结果见表3,不同发射任务条件下仿真曲线簇的终端入轨根数偏差如图9所示。根据表3可得,半长轴偏差的数学期望值小于百米级,标准差小于200 m;偏心率的数学期望值与标准差达到10-4量级;轨道倾角的数学期望值达到10-3(°)量级,标准差达到10-2(°)量级。末修级燃料的平均值为6.5757 kg,最大值为14.761 kg,标准差小于1.7213 kg。数据结果表明,本文所提制导算法对制导关机的液体末修发动机依赖不强,对耗尽关机的固体发动机依然具有高精度终端约束能力。
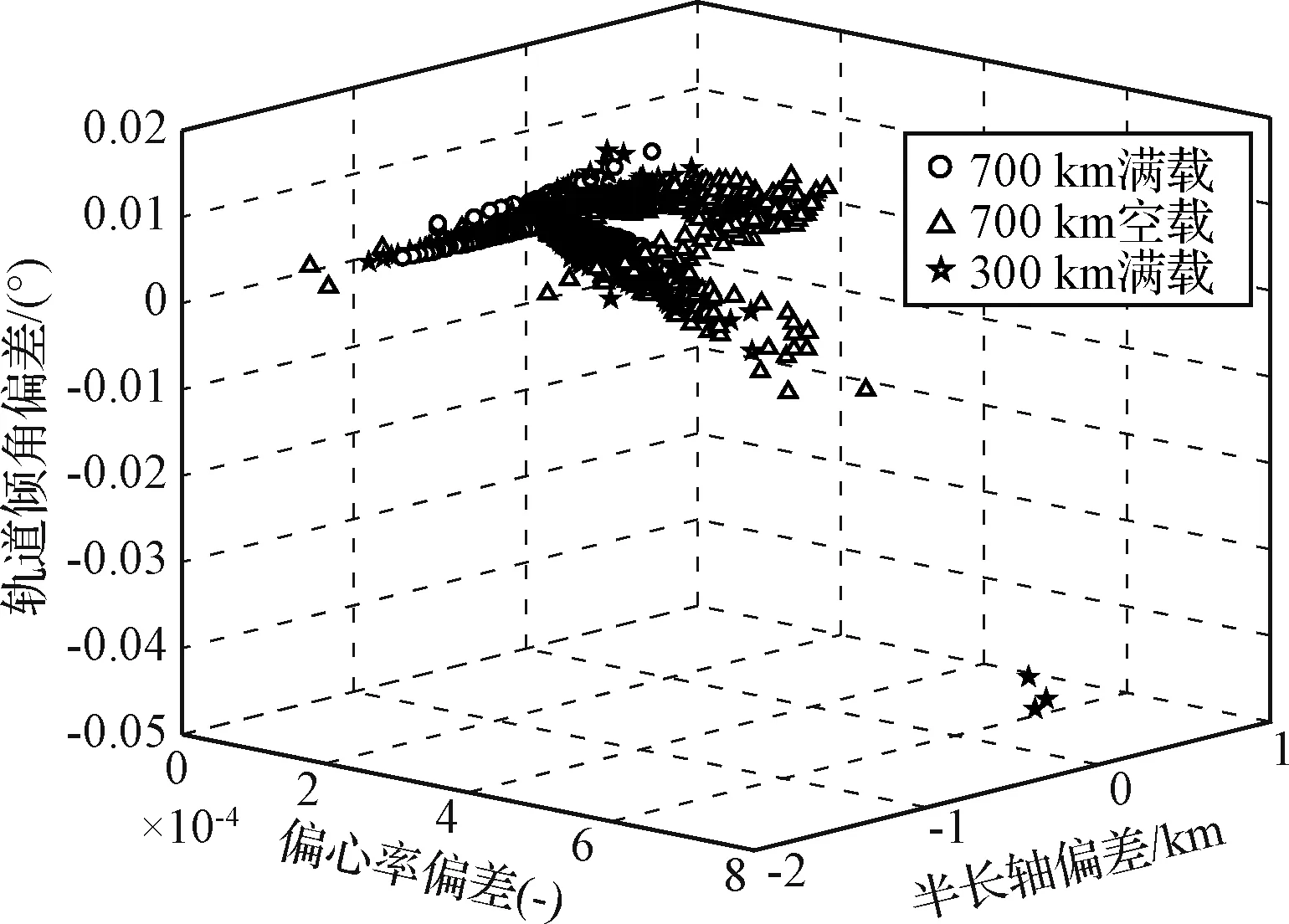
图9 终端轨道要素偏差散布Fig.9 Drogue deployment accuracy
5 结 论
1) PA制导算法根据轨道动量矩矢量方程并引入了速度矢量及位置矢量约束条件,推导出点火时间令与推力矢量求解方程,具有终端多轨道要素约束能力。
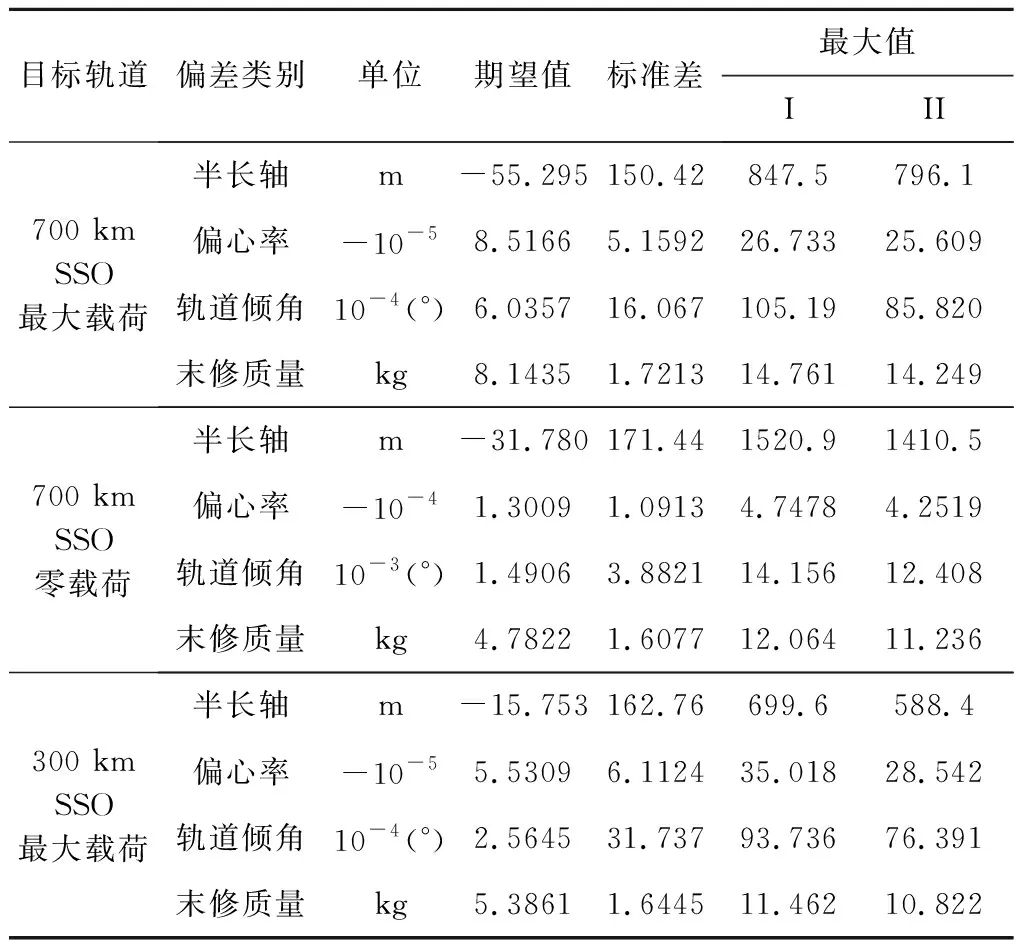
表3 蒙特卡洛仿真统计结果Table 3 Monte Carlo simulations statistic results
2) 多级改进PA算法,通过具有轨道能量约束的滑行过渡轨道建立多级能量匹配方程组,针对不同的发射任务具有在线解算制导指令并满足耗尽关机多终端约束的能力。
3) 在载荷最大条件下,运载火箭几乎无剩余能量,因此消耗末修级燃料较多;而在剩余能量过多的条件下,干扰源的影响使耗尽关机点存在状态偏差并通过滑行轨道进一步放大,使制导算法的鲁棒性降低。
4) 整体制导方案具有很高的制导精度,对所配置的干扰源具有很强的鲁棒性,对不同的发射任务要求具有很强的自主性。
