认知结构模型机动目标跟踪算法

王树亮，毕大平，刘 宝,2，杜明洋

(1. 国防科技大学电子对抗学院，合肥 230037；2. 73676部队，江阴 214400)

0 引 言

现代战场环境中，雷达目标跟踪已经发展成为具有显著复杂性特征的系统建模与处理问题。目前，对机动目标跟踪建模主要有两个方向[1]，一是多模型算法，也称为结构自适应方法，典型的有交互式多模型(Interacting Multiple Model，IMM)算法和变结构多模型(Varied Structure Multiple Model，VSMM)算法，其前提是要寻找合适的模型集，计算过程中代价比较大[2]；另一类是单模型算法，也称为参数自适应方法，典型的有Singer模型、Jerk模型和“当前”统计(Current Statistic，CS)模型等，然而此类算法的模型参数往往需要根据经验提前假定，滤波性能受模型参数的影响比较大[3-4]。

传统雷达通常采用固定的发射信号或者按照某种工作模式周期性地发射信号，通过对接收端处理机制的选择与设计提高雷达性能[5]，即基于回波数据以开环方式工作，这种仅仅依靠基于回波数据的接收端被动自适应处理越来越难以应对复杂时变且无法预知的雷达工作环境。认知雷达[6]将脑科学和人工智能融入雷达系统，赋予了雷达系统感知环境、理解环境、学习、推理并判断决策的能力，使雷达系统能够适应日益复杂多变的电磁环境，从而提高雷达系统的性能[7]。基于控制理论和信息理论，许多学者对面向目标跟踪的自适应波形选择技术如波形库的设计、波形选择准则以及波形参数对跟踪影响等进行了深入研究[8-14]。在传统认知雷达基础上Haykin将人类“记忆、注意、智能”等认知过程充分融入雷达信号及数据处理，使雷达跟踪系统具有更加广泛的认知属性[15]。文献[16]在研究认知控制理论时，基于信息理论，提出用感知信息熵来表征雷达对目标的跟踪质量，其中感知信息熵用滤波误差协方差的行列式来简化等价表示。文献[9]指出机动目标跟踪误差由目标运动误差椭球(圆)和量测误差椭球(圆)相交的区域大小决定。为提高系统跟踪性能，一方面要不断优化机动模型，减小运动误差椭球(圆)体积；另一方面通过波形选择技术使量测误差椭球(圆)与运动误差椭球(圆)保持正交。

受认知雷达研究成果的启发，本文提出一种基于认知结构模型的机动目标跟踪算法，算法综合考虑目标机动模型构建和波形量测的优化，1)将“记忆”模块嵌入到雷达接收端来动态感知环境和目标特性，通过神经网络离线学习生成记忆并存储，指导机动模型参数的实时调整，使模型对运动状态变化的描述更加准确；2)基于人类认知“感知-行动”循环思想，用感知信息熵来描述目标跟踪不确定性，并将其作为波形选择的代价函数，从波形库中自适应选择最佳波形来匹配目标，从而使目标的跟踪性能得到明显提升。

1 认知雷达跟踪模型

1.1 数据处理模型

1.1.1线性状态模型

目标运动的离散状态方程表示为

X(k)=Φ(k|k-1)X(k-1)+

(1)

1.1.2量测模型

目标的量测方程为

Y(k)=H(k)X(k)+Vθ(k)

(2)

1.2 信息熵不确定模型

目标运动和环境变化构成了一系列的不确定性问题，从信息论的观点出发，可以将雷达对目标运动特性的感知用信息熵来表示[16]

E(k)=f(p(X(k)|Y(k)))

(3)

(4)

如果跟踪模型绝对准确且环境为理想环境，即p(X(k)|Y(k))趋近于1，此时信息熵E(k)趋近于0，但实际上由于环境和目标运动的不确定性永远存在，100%的精确也不存在，所以熵的值不可能为0。评价一个模型跟踪性能的好坏可以由信息熵来表征，其值越大，性能越差，反之则性能较佳。认知雷达的显著特点就是将信号处理与数据处理结合起来进行研究，而感知信息熵就是它们联系的一个桥梁。文献[16]给出了信息熵的简化表达式

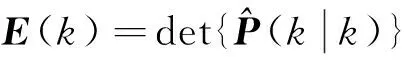
(5)

2 嵌入“记忆”的机动模型构建

2.1 CS模型

模型的基本思想是在每一种具体的战术场合，人们所关心的仅是机动加速度的“当前”概率密度，其概率密度由修正的瑞利分布描述[17]。

(6)

(7)

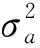
文献[19]利用一个反映当前加速度与加速度极限值匹配程度的高斯隶属度函数L(k)来加权调整加速度极限值，

(8)

式中，ε1,ε2∈[20,25]为实验后得到的经验值，此时amax←L(k)·amax。该修正算法在加速度极限值设置不太大时取得了不错的效果，然而对于非合作目标，加速度极限值往往取较大的值以保证对目标不失跟，此时若当前估计加速度很小或为0，式(8)可能会产生一个很小的L(k)，使amax过小，导致对机动目标失跟。为克服文献算法存在的问题，本文提出一种嵌入“记忆”的CS模型，在考虑当前加速度匹配程度信息的基础上，利用神经网络融合滤波的历史信息来产生一个合适的加速度极限值加权因子。

2.2 嵌入“记忆”的CS模型

记忆是是人类认知的重要过程，它通过从环境中不断地学习而获得知识或经验以有效指导人类行为。记忆的信息处理过程本质上就是“把输入数据映射到一个合适的输出集”，神经网络一般被认为是构建认知雷达中记忆的优秀工具。

通过神经网络这一工具将记忆嵌入CS模型，就是要通过对目标运动特性的实时感知，输出一个机动调整因子来加权加速度极限值，从而减弱模型参数提前假定不合理所带来的影响。本文采用单个卡尔曼滤波器，融合能够充分反映机动特性的速度当前变化以及归一化新息对加速度极限值做调整。算法首先对两属性参数进行提取，作为神经网络的输入参数，通过训练好的网络对自适应滤波的系统方差进行调整。

2.2.1神经网络的输入参数

a)速度的当前变化

选取当前速度变化,即当前加速度(Acceleration)作为神经网络的一个输入(Input)特征参数，来衡量其与加速度极限值的匹配程度，为使其分布于[0,1]之间，根据文献[18]对CS模型加速度适用范围的描述，将其表示为

Ainput(k)=

(9)

b)归一化新息

首先定义k时刻归一化新息的平方为

εv(k)=vT(k)S-1(k)v(k)

(10)

(11)

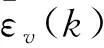
(12)

为便于神经网络训练，使输入值(Input)分布于[0,1]之间，故将其变换为

(13)

式中，B为门限值。

2.2.2神经网络结构及输出

神经网络选取基于误差反向传播的BP网络，该神经网络具有很强的非线映射能力，一个3层BP神经网络能够实现任意非线性函数的逼近。选取输入节点数为2，即速度变化Ainput(k)和模型匹配度变量Minput(k)，传递函数为双曲正切S型传递函数，隐层节点数设为8，输出节点数为1，即输出Ooutput。其网络结构如图1所示。

图1 3层BP神经网络结构Fig.1 Three layers BP neural network

CS模型在实际跟踪中，为了确保能及时地追踪战场目标的“机动”变化，往往以牺牲对弱机动目标的跟踪精度取较大的加速度极限值，此时，若Ainput(k)较小，说明当前加速度极限值设置过大，应输出一个小的加权因子，反之则应输出一个大的加权因子；若Minput(k)较小，说明过程模型匹配较好，加速度极限值设置合理，此时输出一个较大的加权因子，这就避免了若当前加速度估计不准确而陷入局部最优的情况。经过神经网络调整因子Ooutput加权后的加速度极限值为a±max←Ooutput·a±max。

3 基于“感知-行动”循环的波形选择跟踪算法

3.1 波形库及代价函数

量测误差协方差Rθ(k)与发射波形参数θ有关，采用量测噪声协方差参数估计的克拉罗下界来表示，取发射信号为高斯包络线性调频信号形式即[8]

(14)

式中，λ为信号的有效持续时间；b为频率调制率。其距离、速度测量误差协方差的表达式为

(15)

式中，η为信噪比，c为电磁波速度，fc为载频。波形库是在雷达工作之前事先需要设计的，可以想象波形库为二维网格，每一个网格代表一个可用的波形，网格位置由(λ,b)唯一确定。波形库WB可以表示为

WB={λ∈[λmin:Δλ:λmax],b∈[bmin:Δb:bmax]}

(16)

式中，下标min和max表示设计好的参数的最小值和最大值，Δ为参数的取值步长。

波形库设计的目标是能够提供有限的波形以满足跟踪需要。从信息论角度出发，选择波形的目标是使下一个时刻模型的概率分布熵最小，也就是模型和量测之间的互信息最大。当量测误差椭球(圆)与目标状态预测误差椭球(圆)正交时，波形是最优的[9]，如图2所示。

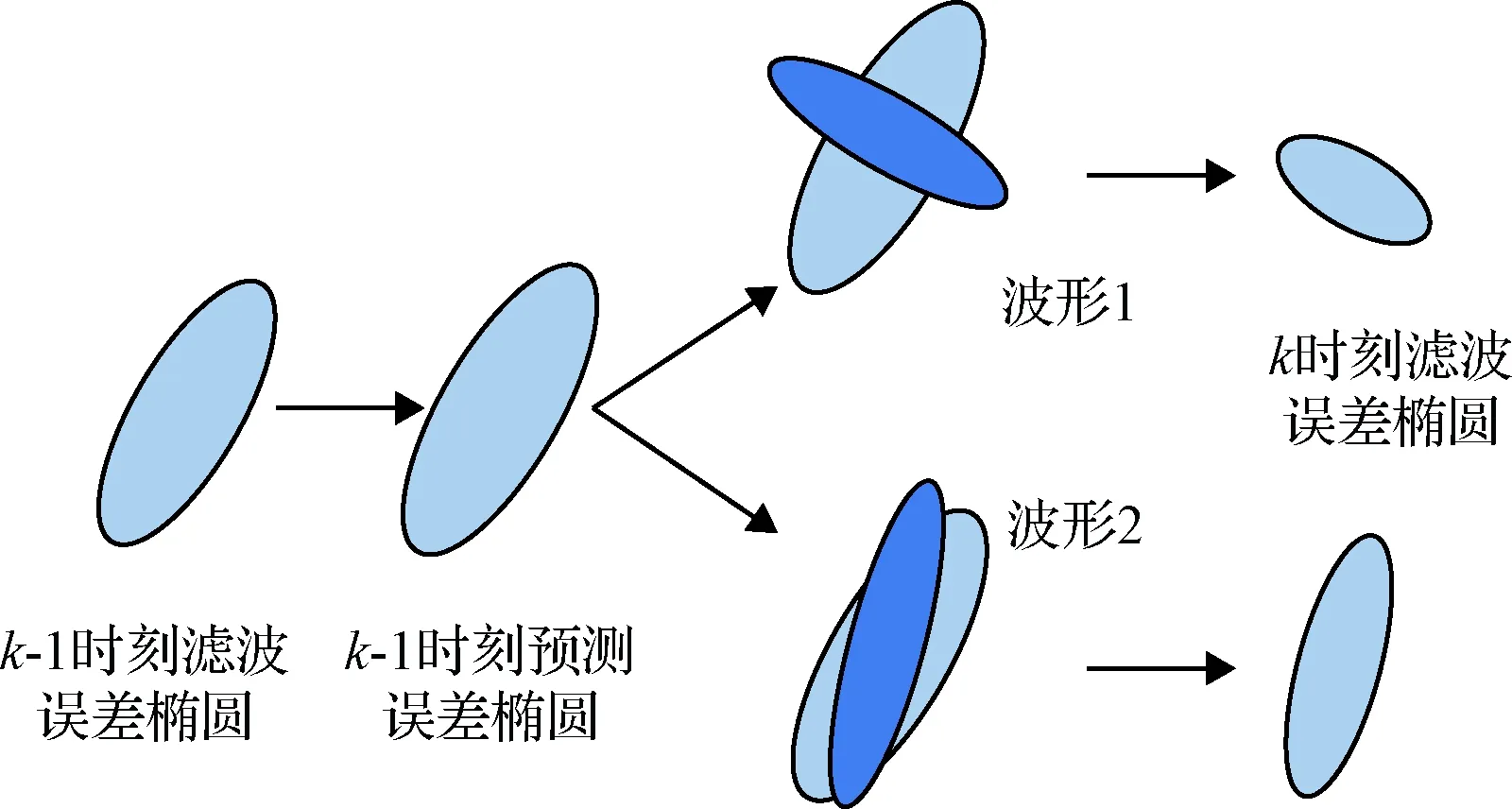
图2 不同波形目标跟踪效果Fig.2 Tracking effect of different waveform

根据1.2节感知信息熵不确定性的描述，基于信息熵准则的代价函数可描述为

(17)

3.2 基于“感知-行动”循环的波形选择跟踪流程

“感知-行动”循环是人类的认知过程，体现在雷达目标跟踪中，其信息流循环如图3所示，有以下3个基本步骤

a)发射机在k-1时刻向环境中发射具有一定参数θk-1的波形，得到相应测量精度的量测Y(k-1)；

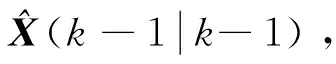
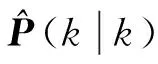
图3 认知雷达跟踪信息流循环图Fig.3 Information flow of cognitive radar

4 仿真校验

4.1 仿真设置

假设雷达发射波形载频为10.4 GHz，发射信号采用式(14)所描述的波形。雷达位于直角坐标原点，波形库内脉冲有效持续时间λ选择范围为[2×10-6,20×10-6]s，间隔为2×10-6s；调频斜率b的范围是[-30×107,30×107]Hz·s-1，间隔为5×107Hz·s-1；雷达系统的信噪比设为16 db。

4.2 仿真对比及分析

a)固定波形算法对比

采取固定波形(λ=4×10-6s,b=0)，对比CS模型算法，文献[16]算法以及本文提出的嵌入记忆的CS(Memory Current Statistic，MCS)模型。假设模型机动频率常数为1/60，检验统计量的样本数N设为20，B取值为0.4。进行50次Monte Carlo仿真实验。

图4(a)、(b)分别为20个采样周期后利用MCS算法加速度匹配和模型匹配输入的动态变化曲线，图4(c)为网络输出加权因子的动态输出曲线。表1给出三种算法在最大加速度取30，40，50，60 m·s-2时的距离、速度估计均方根误差的均值(Average Root Mean Square Error，ARMSE)。

由图4 (a)、(b)实时输入参数变化曲线看出，阶段2、阶段3和阶段4中加速度匹配参数相比阶段1、阶段5明显较小，而模型匹配参数则相对较大，反映了目标的机动性较弱且模型匹配度较差，此时输出相对小的权值因子(如图4 (c))；而在强机动阶段(阶段1、5)，则输出一个接近1的输出因子。由表1不同加速度极限值情况下三种算法距离估计ARMSE对比可知，随着加速度极限值的增大，三种算法的跟踪误差都有所增大，CS模型的跟踪误差增大最为明显，反映了算法对加速度极限值的依赖；文献[19]算法在加速度为40 m·s-2以下时，由于高斯隶属度函数L(k)的加权调整其跟踪性能得到明显改善，而且要优于MCS算法，然而当其加速度极限值继续增大时，由于加权函数本身存在的问题，可能导致目标失跟，误差较大；本文MCS算法充分考虑了当前加速度和滤波的历史信息，避免了因为当前加速度估计不准确可能陷入的局部最优情况，其鲁棒性要优于文献[19]算法。

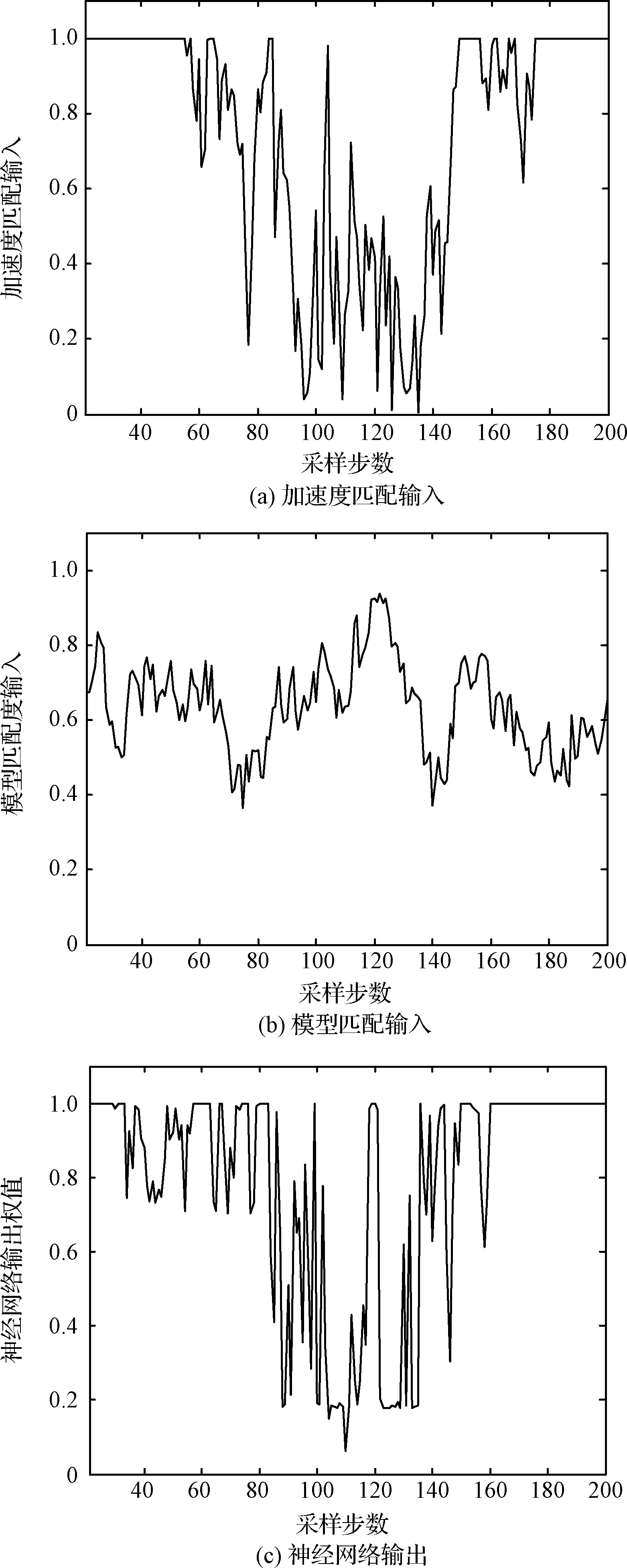
图4 神经网络输入和输出Fig.4 Input and output of the neural network

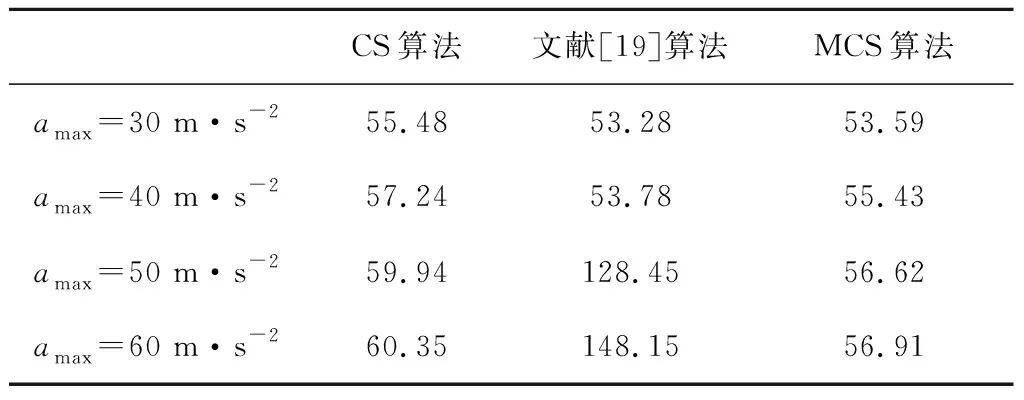
Table 1 Comparisons of range ARMSE for the three algorithms (m)

b)自适应波形算法对比

比较采取固定波形(波形1参数为λ=4×10-6s, b=0；波形2参数为λ2=10×10-6s,b=0)的CS模型算法以及采取基于波形选择的MCS(WS-MCS)模型算法的滤波性能，指标选取距离、速度的估计均方根误差(Root Mean Square Error，RMSE)，状态感知不确定性信息熵，仿真结果由50次Monte Carlo实验统计得到。

图5分别为自适应波形跟踪算法和固定波形跟踪算法距离、速度RMSE对比曲线。图6为波形动态自适应选择情况，图7为三种算法的状态感知信息熵对比曲线。

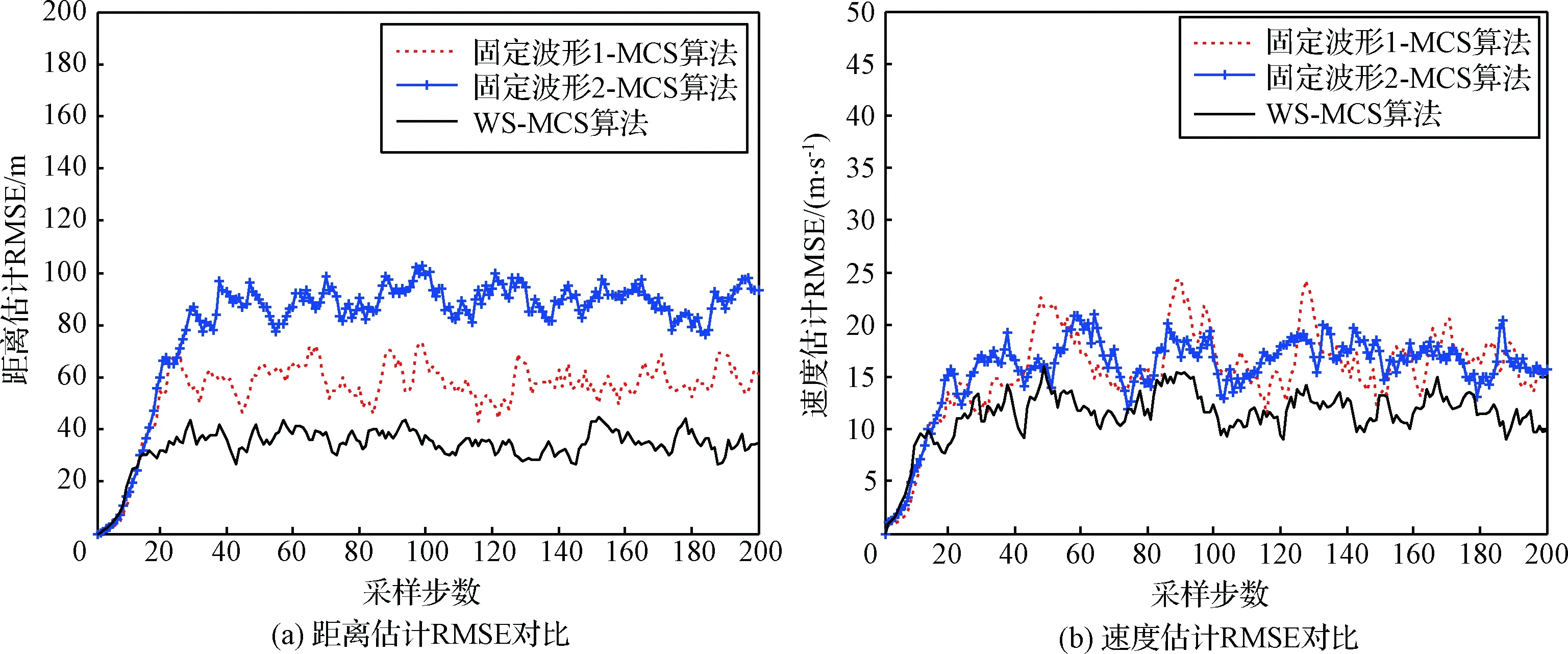
图5 距离和速度RMSE对比Fig.5 Comparisons of range and velocity RMSE

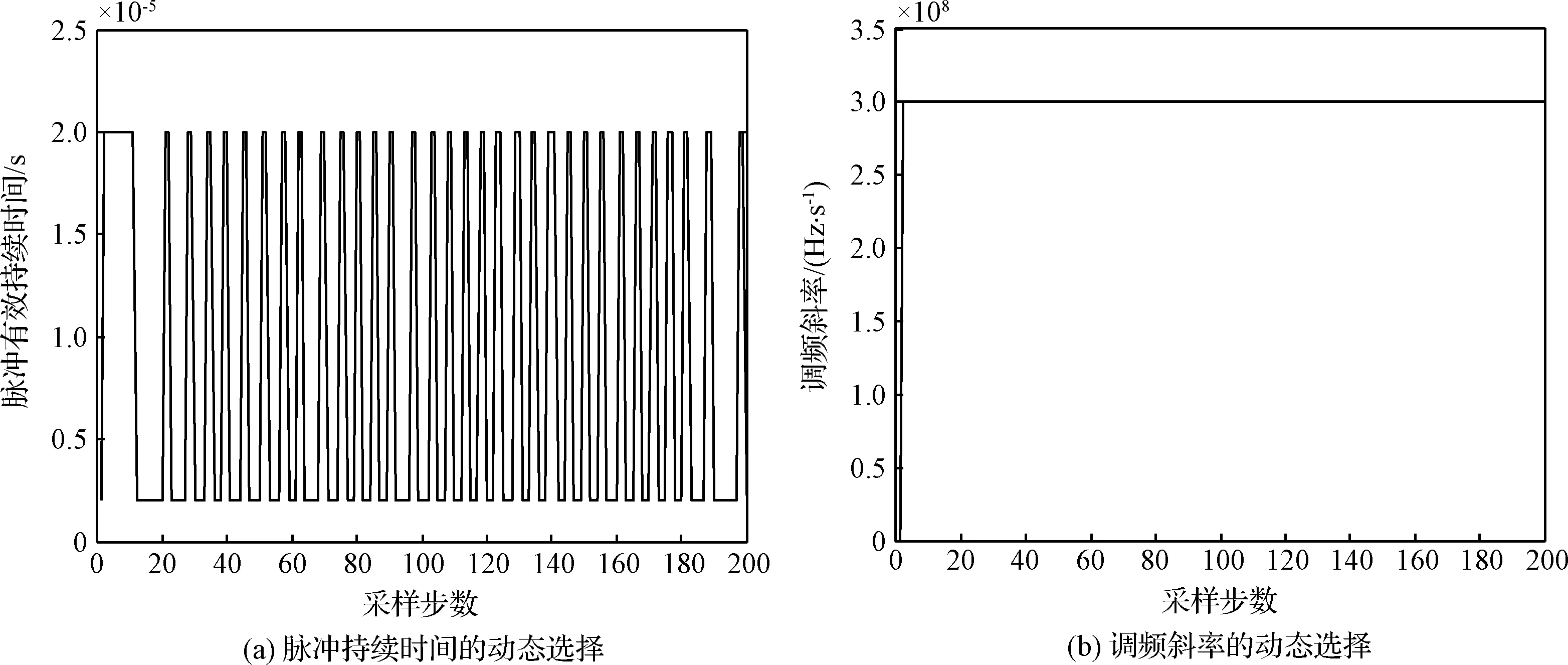
图6 波形动态选择Fig.6 Waveform dynamic selection

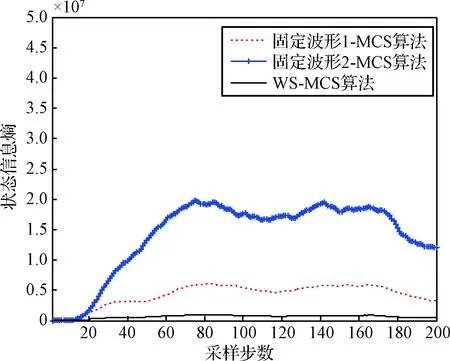
图7 跟踪状态不确定性对比Fig.7 Comparison of tracking state uncertainty

波形1-MCS波形2-MCSWS-MCS距离ARMSE/m54.7181.5833.62速度ARMSE/(m·s-1)15.5015.3211.37

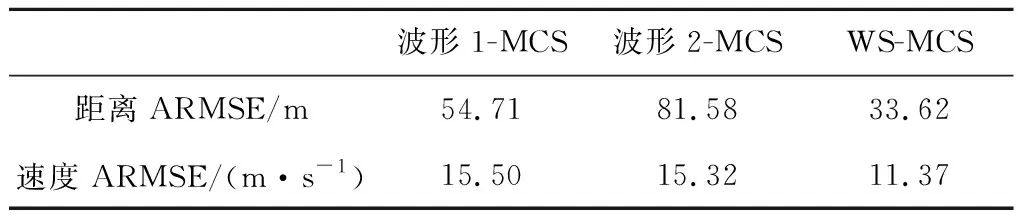
由图5和表2可以看出，选用固定波形1的算法，相比波形2算法因为其有效脉冲持续时间较小，其距离量测精度较高、测速精度较差，所以使得距离跟踪误差较小，但速度跟踪误差较大。由图6波形自适应选择曲线可知，调频斜率取正的最大值，使量测误差椭球(圆)与运动误差椭球(圆)尽量保持正交，而脉冲有效持续时间除在开始阶段选择第10个波形，其余时刻在第1个波形和第10个波形之间交替转换，持续平衡距离测量误差和速度测量误差，以使误差椭球(圆)相交区域的体积(面积)最小，这在图7跟踪不确定性对比曲线中反映得非常明显，总体上看，波形1要优于波形2，自适应波形跟踪精度要明显优于采取固定波形的方法，且在跟踪稳定性上也明显较优，鲁棒性较强。

5 结 论

本文所提出的跟踪算法，实质上是雷达接收端机动模型和雷达发射端波形的全自适应认知结构模型算法。算法将人类认知中的“记忆”过程嵌入到雷达接收机前端来动态感知目标运动特性，从而提出一种嵌入“记忆”的“当前”统计模型，该模型能够通过离线训练好的神经网络有效指导模型中系统方差的自适应调整，仿真结果验证了模型对目标机动运动的描述更为合理有效，基于信息熵最小准则的波形自适应结构也明显优于采取固定波形结构的方法。由于篇幅受限，仅研究了认知结构单机动跟踪模型以及波形自适应机制，对认知结构的交互多模型还有待在以后的研究中继续探讨。