木星辐射环境不确定性对总剂量风险的影响

王建昭，张庆祥，郑玉展，田 岱

(北京空间飞行器总体设计部，北京 100094)

0 引 言

木星是太阳系中最大的行星，且拥有数量众多的卫星，对其探测有助于解决太阳系形成、演化等重要科学问题。美国、欧洲已有多颗探测器造访过木星[1-4]，且还有多个木星探测计划正在论证和实施。同时，木星探测也是我国未来深空探测的热点之一，已有一些关于任务规划和轨道设计的研究成果[5-6]。与其他深空探测相比，木星探测的难点之一是其恶劣的辐射环境[7]。平均而言，木星磁矩是地球的2×104倍。以木星赤道面4Rj(木星半径，取71 492 km)轨道和地球GEO轨道为例，木星辐射带低能质子(0.1～0.5 MeV)通量是地球的10倍，高能电子(1～5 MeV)通量比地球高2～3个数量级。因此，辐射防护在木星探测中十分重要。辐射防护需要保证航天器运行期间电子元器件不因粒子辐射而失效，其中总剂量效应[8]和内带电效应[9]是比较严重的。

在设计中，需要为辐射造成的总剂量的不确定性留有余量，一般工程上采用辐射设计余量(radiation design margin, RDM)进行控制和设计[10]，RDM的值是平均辐射失效值(用RMF表示)和寿命周期辐射规范值(用RSPEC表示)的比值。利用RDM进行评估的流程如图1所示。首先，根据任务需求计算航天器舱内和舱外的辐射环境，再以此为输入计算舱内吸收体的辐射剂量RSPEC；选择电子元器件，并根据已有试验数据得到器件的平均失效辐射剂量值RMF；再根据设计规范规定的RDM进行分类，如果能满足RDM控制要求，则认为已符合防护要求，如果不能满足要求，则需进行额外的辐射防护，如增加屏蔽层厚度等。

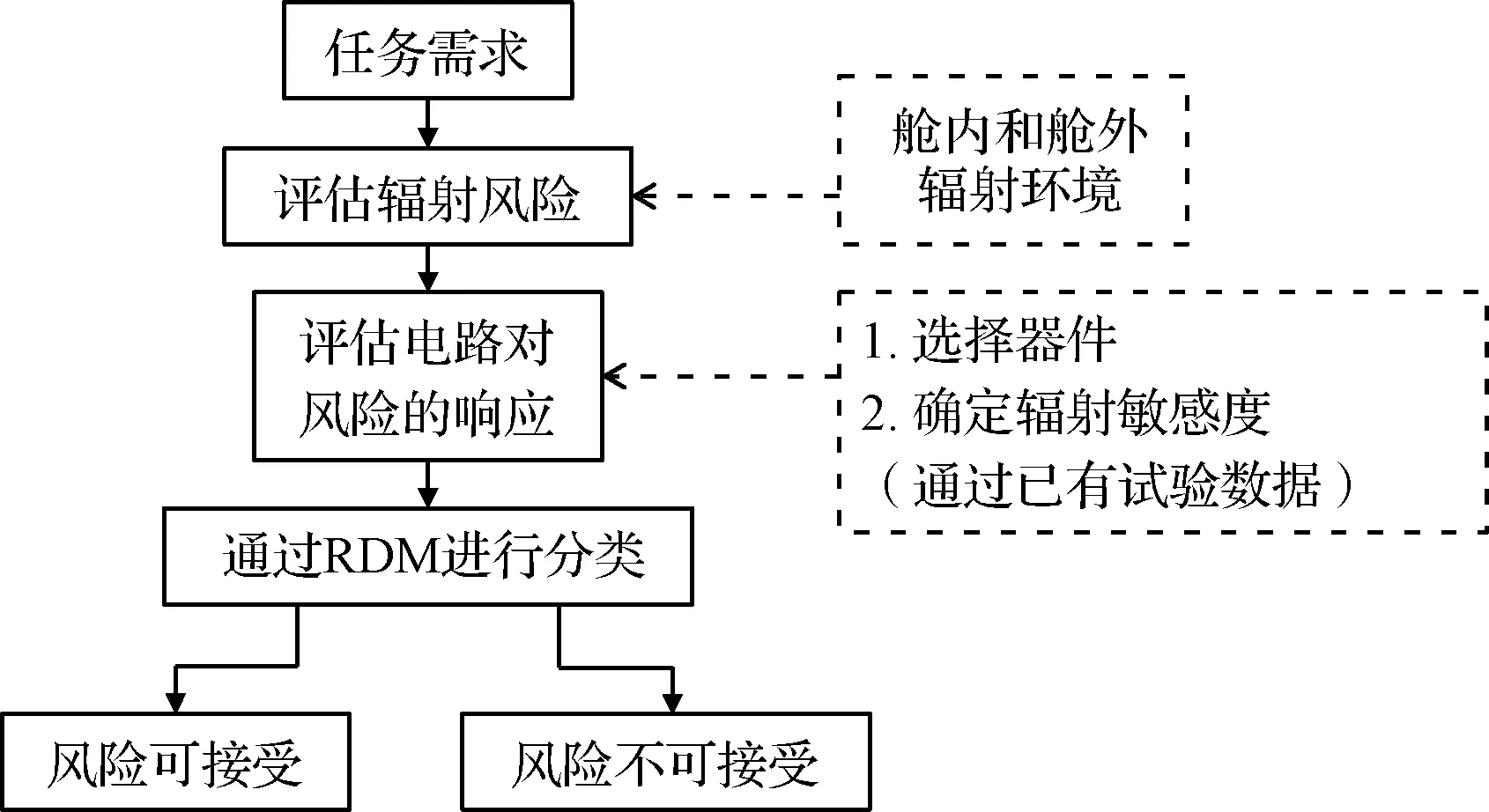
图1 利用RDM评估总剂量风险的流程Fig.1 The flow chart of total dose evaluation by RDM method

RDM是基于工程规范的设计方法，其数值选择具有一定主观性。首先，空间辐射环境具有不确定性，RDM设计方法假设任务期间辐射剂量是定值，而没考虑辐射环境的动态变化，某一RDM值对应的置信度及RDM数值选择需要具体考虑。另外，利用历史数据对未来任务进行评估存在一定风险。Ladbury等[11]通过统计方法，利用不同器件历史数据，得到不同存活概率及其对应置信度下所需要的最低RDM值。

除此之外，不同批次及不同器件的失效剂量有一定不确定性和随机性，常用正态分布、对数正态分布、威布尔分布拟合[12]。如果器件失效剂量和空间环境剂量的不确定范围相近，器件特性对辐射环境变化十分敏感，需要特别考虑特定器件的辐射失效特性。Xapsos等[13]提出了一种将空间环境不确定性和器件失效总剂量不确定性相结合的方法，可定量评估一定屏蔽厚度下特定器件的失效概率。

木星系中带电粒子不仅能量高、通量大，且不确定性大，这加大了航天器辐射剂量效应的防护难度。根据Galileo探测器EPD仪器探测结果[14]，相同L值处最高的粒子通量比最低时大4倍，且随着距木星中心距离的增加，粒子通量的不确定性增加，如应用常规的RDM设计手段规避器件失效，导致的屏蔽质量代价高昂，因此需要优化RDM选择方法。另外，木星探测周期长、风险大，对于关键元器件，还需要精细分析其在轨失效特性。

在木星探测任务中，辐射剂量的主要来源包括：辐射带高能质子与电子、太阳宇宙线。对于太阳宇宙线，主要贡献来自太阳高能粒子事件，其中质子通量占绝大部分(90%以上)。因此，评估木星探测任务的辐射剂量，需要木星辐射带模型和太阳质子通量模型。本文试图利用已有模型，将木星辐射环境的不确定性应用于木星环绕任务的总剂量效应及风险评估中，提出了一种基于不确定度的风险控制方法。

1 考虑不确定性的失效概率分析方法

1.1 器件失效率评估方法

器件在辐射下的失效剂量符合一定分布，假设在总剂量辐照试验中，同时对多个相同器件进行辐照，G(x)为测量得到的失效累计分布函数(cumul-ative distribution function, CDF)，其中，x为剂量点值且由试验确定，G(x)表示在该剂量点已失效器件占器件总数的比例，g(x)为对应的概率密度函数(probability density function, PDF)。对于空间真实辐射环境的动态变化，利用各置信度下的辐射通量，可得到该置信度下任务周期内所受空间辐射剂量的CDF为H(x)，H(x)表示在特定条件下器件在空间中所受辐射剂量小于x的概率，相应的PDF为h(x)。

假设空间中辐射剂量和地面试验辐射剂量等效，即试验得到的器件失效规律同样可应用于空间辐射。而实际上，地面试验所用粒子源一般是单能单一粒子、单方向且高剂量率的，而空间真实情况是多种能量多种粒子、各向同性及低剂量率的。将两种分布函数结合，可得到任务周期内，器件在剂量x到x+dx之间的失效概率为：

[1-H(x)]·g(x)dx

(1)

式中：[1-H(x)]为器件所受剂量大于x的概率。经过积分，可以得到任务周期内，在该屏蔽条件下器件由于总剂量效应而失效的概率P：

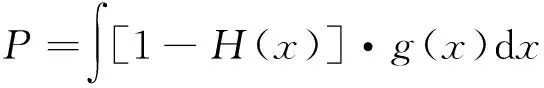
(2)

1.2 器件失效剂量数据获取

对于商业器件，即使任务期内粒子辐射强度不高，也应详细考察总剂量失效特征。一般来说，对于不同器件，其性能随辐射总剂量的衰减规律很不相同，不同批次间的平均失效剂量及其标准偏差的分布有很大差异[12]。为考察器件失效剂量和辐射环境不确定性的关系，应尽量选择辐射剂量敏感器件，且存在一定的失效剂量分布区间。在本文中，选择一种典型的商用数据采集功能模块器件TL084，对其进行地面辐照试验。对于TL084，利用60Co-γ射线辐射源进行总剂量效应试验。该放射源由若干根60Co源棒组成，源棒排列成圆柱状，如图2所示，该排列方法保证在有效区域内，辐射源场的不均匀性小于10%,，实验方法如文献[15]。

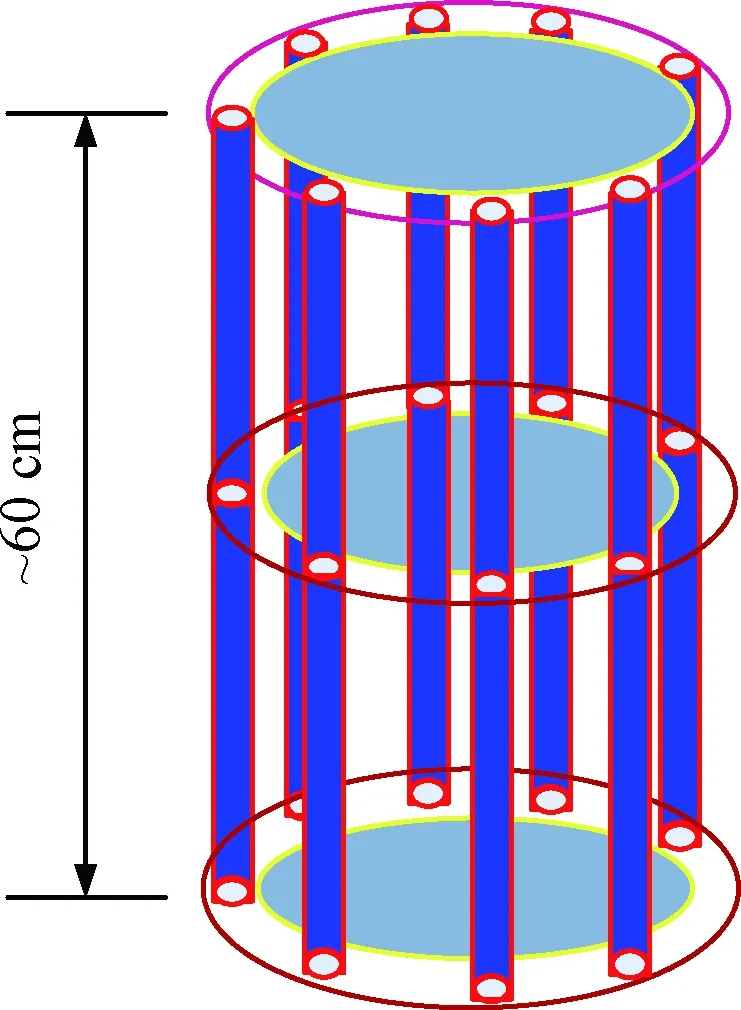
图2 60Co-γ放射源立式结构示意图Fig.2 The vertical structure of 60Co-γ radiation source

辐照试验剂量率为50 rad(Si)/s，最大辐照量为100 krad(Si)(该剂量可保证TL084器件完全失效)，共均匀设置5个剂量点，对应辐照时间为33.3分钟。试验中，同时对8个相同器件进行辐照。根据国标QJ 10004—2008[16]，在不知道器件最恶劣偏置时，也可采用应用偏置条件。因此，在本实验中，每个器件都施加正常工作电压，以保证每个器件受到的辐照及状态相同。测量TL084正偏置电流随总剂量的变化，如图3所示，每个器件的正偏置电流随辐照剂量的变化关系存在一定差异。

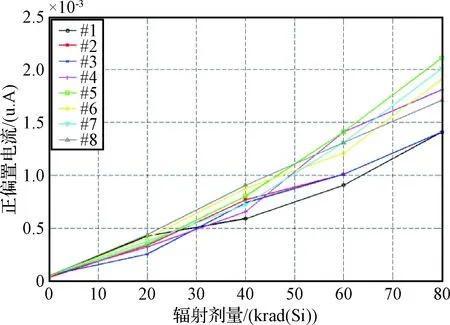
图3 TL084正偏置电流随总剂量的变化Fig.3 The positive bias currents of TL084 versus total dose

当正偏置电流增加到一定程度时，TL084器件性能参数异常而认为器件失效。在本文中，当正偏置电流增加1000倍(1×10-3μA)时认定器件失效。将试验数据进行差分得到每个器件的失效剂量，再将每个失效剂量值递增排序，用m/(N+1)表示该剂量下的失效累计发生概率，其中m是排列序号，N是器件数量(N=8)。由于辐照试验代价高昂，为了得到一般规律，将得到的累计失效概率分别用正态分布、对数正态分布、威布尔分布进行拟合。为了考察该拟合的优度，定义决定系数R2：

(3)

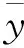
据拟合结果，威布尔拟合的决定系数R2为0.863，高于其他类型拟合，因此采用威布尔分布，即得到了G(x)。将拟合结果画在威布尔分布坐标纸上，如图4(a)所示。图中横轴为对数坐标轴，纵轴为非线性坐标轴，在该坐标轴下威布尔分布为直线。该威布尔分布的PDF即为g(x)，如图4(b)所示，该威布尔分布的偏度为-0.53，即相对于平均失效剂量，较高剂量的失效率相比较低剂量的失效率更大。

表1 TL084累计失效概率拟合的决定系数Table 1 Determination coefficient of TL084 failure CDF fitness

图4 TL084辐射失效概率的威布尔拟合Fig.4 The Weibull fit of TL084 failure possibility

1.3 木星辐射带模型

已有的木星辐射带模型包括：D&G模型[17]、GIRE模型[18]及JOSE模型[19]，其中D&G模型和GIRE模型只能描述木星辐射带平均通量，而JOSE模型可描述不同置信度的粒子通量，该置信度通量通过将平均通量乘以相应系数得到。本文选用JOSE模型，该模型可通过SPENVIS在线进行计算[20]。JOSE模型在离木星较近(L< 9.5)时采用Salammb理论模型，其他区域模型利用Galileo号绕飞木星35圈的局地探测数据构建。

表2 假想木星环绕任务参数Table 2 The parameters of an imaginary Jovian orbiting mission

探测器沿轨道的辐射粒子通量如图5所示。从上到下依次是：不同置信度2 MeV电子积分通量、不同置信度 10 MeV质子积分通量、太阳-木星-探测器夹角(Sun-Planet-Satellite, SPS)。探测器飞行周期为4.5 d，在一个周期内，对于赤道面轨道，SPS在0°至180°之间变化两次。辐射通量随轨道相位有一定变化，这主要来源于木星磁层结构的晨昏不对称性以及木星的快速自转，变化周期约为木星自转周期(约10 h)。

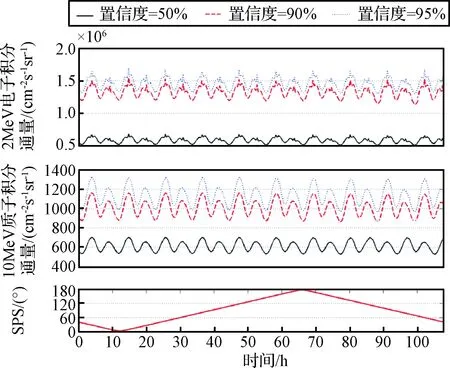
图5 航天器沿轨道辐射通量Fig.5 The radiation flux along spacecraft orbit

1.4 太阳质子通量模型

已有的可用于工程化的太阳质子通量模型包括King模型[21]、JPL模型[22]及ESP模型[23]。本文采用的是李婷婷等[24]基于JPL模型开发的改进版太阳质子通量模型。该模型基于1964-2007年近5个太阳活动周太阳质子事件数据，以太阳黑子年平均数为判据，将太阳活动周分为活动高、中、低年，在一个太阳活动周中，三个时期所占时间约为3∶3∶4。

模型对10 MeV和30 MeV两个能量的积分通量进行了统计，假设太阳质子事件通量fp=10F符合对数正态分布，则F符合正态分布。采用组合概率表示在一段时间τ内，质子通量超过fp的概率：

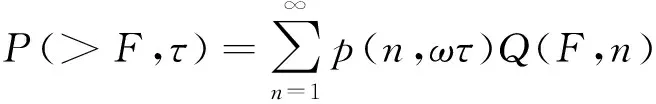
(4)

式中：p(n,ωτ)为时间τ内发生n次质子事件的概率；ω为质子事件的年平均发生次数，按太阳活动水平高低而取不同值，若τ内跨越不同太阳活动强度等级，则通过时间加权得到；Q(F,n)为n次事件通量之和超过10F的概率。

质子事件是相互独立的，其发生概率可以用泊松分布描述：

p(n,ωτ)=e-ωτ(ωτ)n/n!

(5)

一般来说，对于相同的发生概率，任务期越长，质子通量越大；太阳活动强度越大，质子通量越大。而对于特定的质子通量，任务期越长，超过该通量概率越大；太阳活动强度越大，超过该通量概率越大。

将模型用于木星环绕任务的总剂量分析，需要2点假设。首先，该模型对应于地球轨道(1 AU)的观测数据，太阳质子通量随着探测器日心距离的增加而减小，假设通量与日心距离平方呈反比，可得到木星轨道(5.2 AU)的太阳质子通量；其次，该模型只提供10 MeV和30 MeV质子的积分通量，假设太阳质子微分能谱满足能量指数线性关系，即fd(E)=F0×exp(-E/E0)，其中fd是能量为E的微分通量，通过两个能档的积分通量可得到F0和E0的值，进而得到微分通量能谱。

假设任务周期为2018年，此时为太阳活动低年，ω=1.706，τ=1。得到不同置信度下的质子微分能谱如图6所示，随着置信度提升，各能段质子通量显著上升，由于假设能谱关于能量有指数线性关系，各置信度下的能谱形状相同。与图5相比，木星辐射带质子相对太阳质子通量大3个数量级，太阳质子对辐射剂量的影响相对很小。

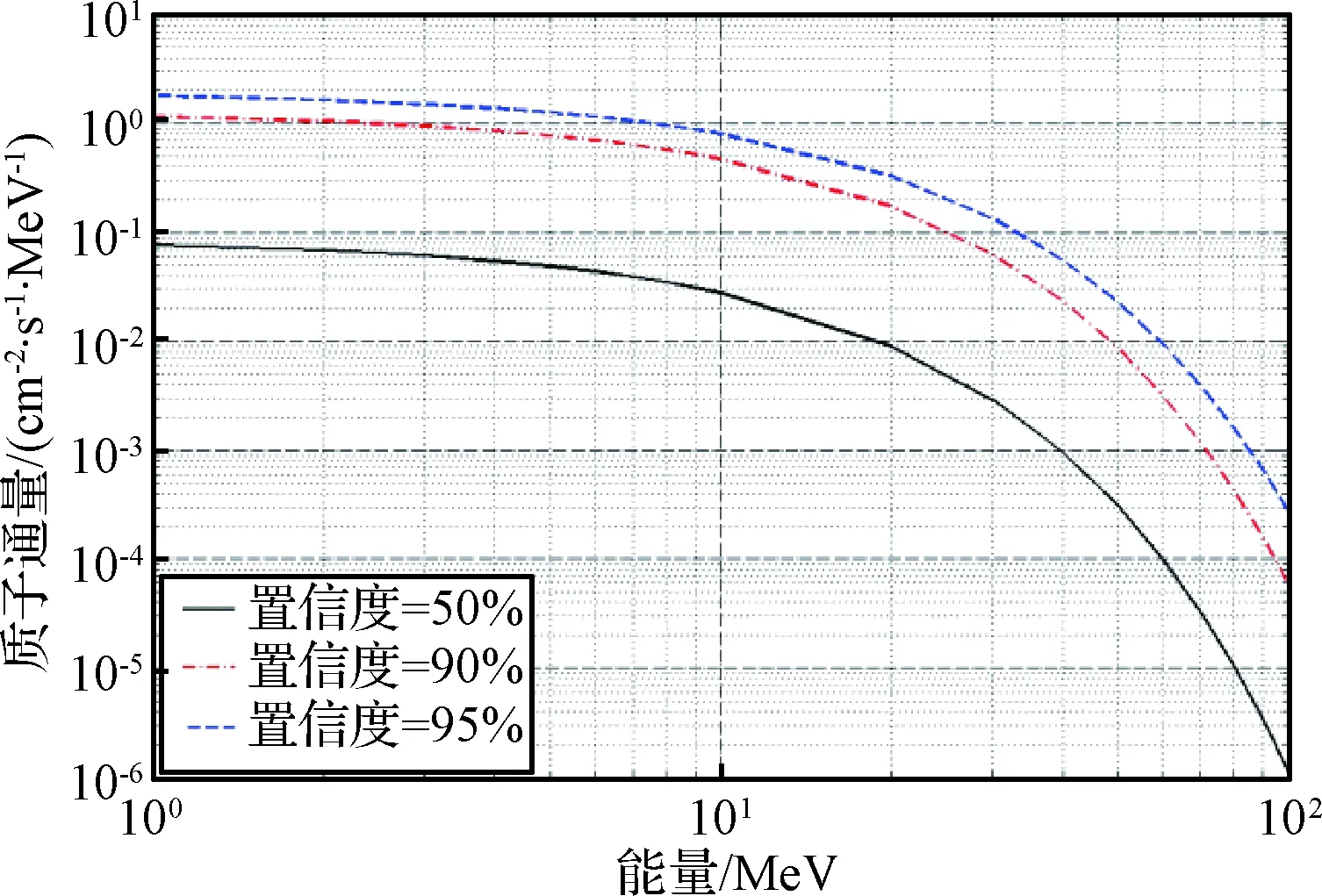
图6 太阳质子微分能谱Fig.6 The differential spectrum of solar proton

2 计算结果

2.1 典型木星任务中的器件失效概率

以木星辐射带质子、电子通量能谱，以及太阳质子通量能谱为输入，利用SHIELDOSE2[25]，选择一维实心球屏蔽模型，计算不同任务期内，不同置信度和不同铝屏蔽厚度下的辐射剂量，1个月任务期辐射剂量如图7所示。图中每条曲线表示该屏蔽厚度下不同剂量对应的累计发生概率，即H(x)。在SPENVIS在线计算程序中，只提供置信度为50%及以上的辐射环境通量，为了得到置信度50%以下的值，本文假设粒子通量分布符合对数正态分布(这一假设与文献[14]中统计结果相同)，即：p(lg(Fmedian-ΔF))=p(lg(Fmedian+ΔF))，其中，Fmedian是置信度为50%的通量，p是发生概率，ΔF是任意增加或减少的通量。因此：

lg(D50+x)-lg(D50)=lg(D50)-lg(D50-x)

(6)

其中，D50+x、D50、D50-x分别为置信度为(50+x)%、50%、(50-x)%的剂量。

平均而言，0.1 mm铝屏蔽后的辐射剂量比2 mm铝屏蔽高1个数量级，且随着屏蔽厚度增加，辐射剂量迅速减小。曲线宽度代表不同置信度引起的剂量变化，在高置信度下(90%以上)，随着置信度增加，辐射剂量的增加幅度相对更大。

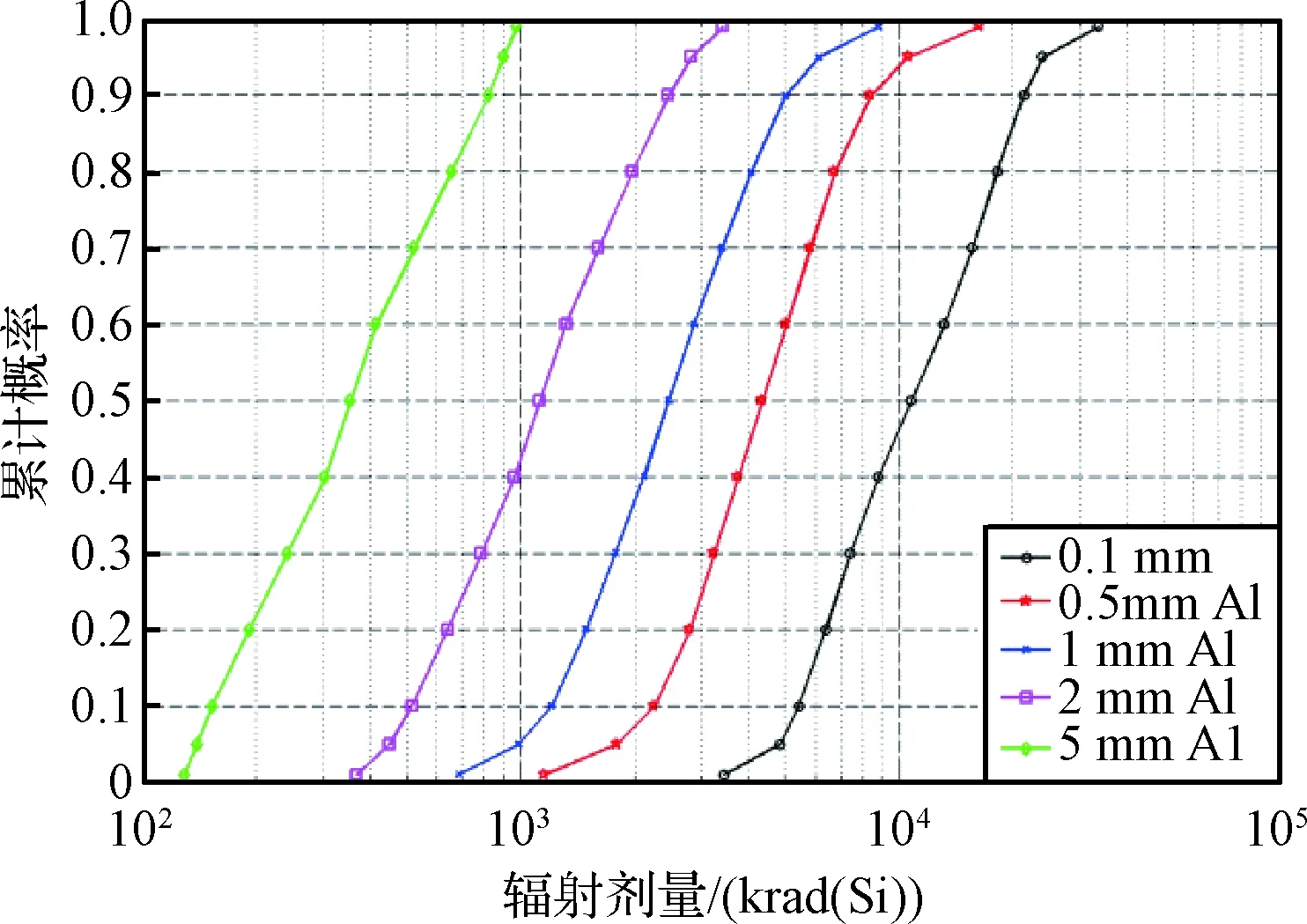
图7 1个月任务期总剂量累计概率分布Fig.7 Total dose CDF for a 1-month Jovian mission

另外，定义辐射剂量曲线宽度w=lg(D99.9-D0.01)，其中，D99.9和D0.01分别是累计发生概率99.9%和0.01%的剂量，宽度w表示由于辐射环境通量不确定性导致的剂量不确定性范围，结果如表3所示。随着屏蔽厚度增加，宽度w减小，这可能是因为，木星中高能质子和电子的通量不确定性范围小于低能质子和电子。屏蔽厚度越大，低能粒子被屏蔽，辐射剂量的主要贡献来自高能粒子，而高能粒子导致的剂量不确定性范围较小。

表3 不同屏蔽厚度剂量曲线宽度Table 3 The width of dose curve after different shields

根据H(x)和g(x)，利用式(2)，即可计算不同屏蔽厚度下由粒子辐射导致的失效概率，如图8所示。该结果将辐射环境不确定性导致的辐射剂量不确定性，与器件失效不确定性相结合，给出了失效概率的分布。失效概率取决于辐射环境剂量不确定性范围和器件失效剂量不确定性范围。以1个月任务期为例，当铝屏蔽厚度小于8 mm时，环境不确定性范围内剂量大于器件不确定性范围内剂量，失效概率为1；当铝屏蔽厚度大于8 mm时，环境不确定性范围内剂量和器件不确定性范围重叠，失效概率为0至1之间；若环境不确定性范围内剂量小于器件不确定性范围，失效概率为0。随着屏蔽厚度增加，失效概率减小，随着任务期减小，失效概率相应减小。在该轨道下，粒子辐射环境十分恶劣，对于2个月任务期，为了使TL084器件失效概率降到可接受范围，所需的屏蔽厚度很大，辐射防护代价高昂。当屏蔽厚度为10 mm铝时，TL084器件平均寿命(以失效概率0.5为判据)仅为1星期至2星期，类似的，当屏蔽厚度为15 mm铝时，TL084器件平均寿命为2星期至1个月。

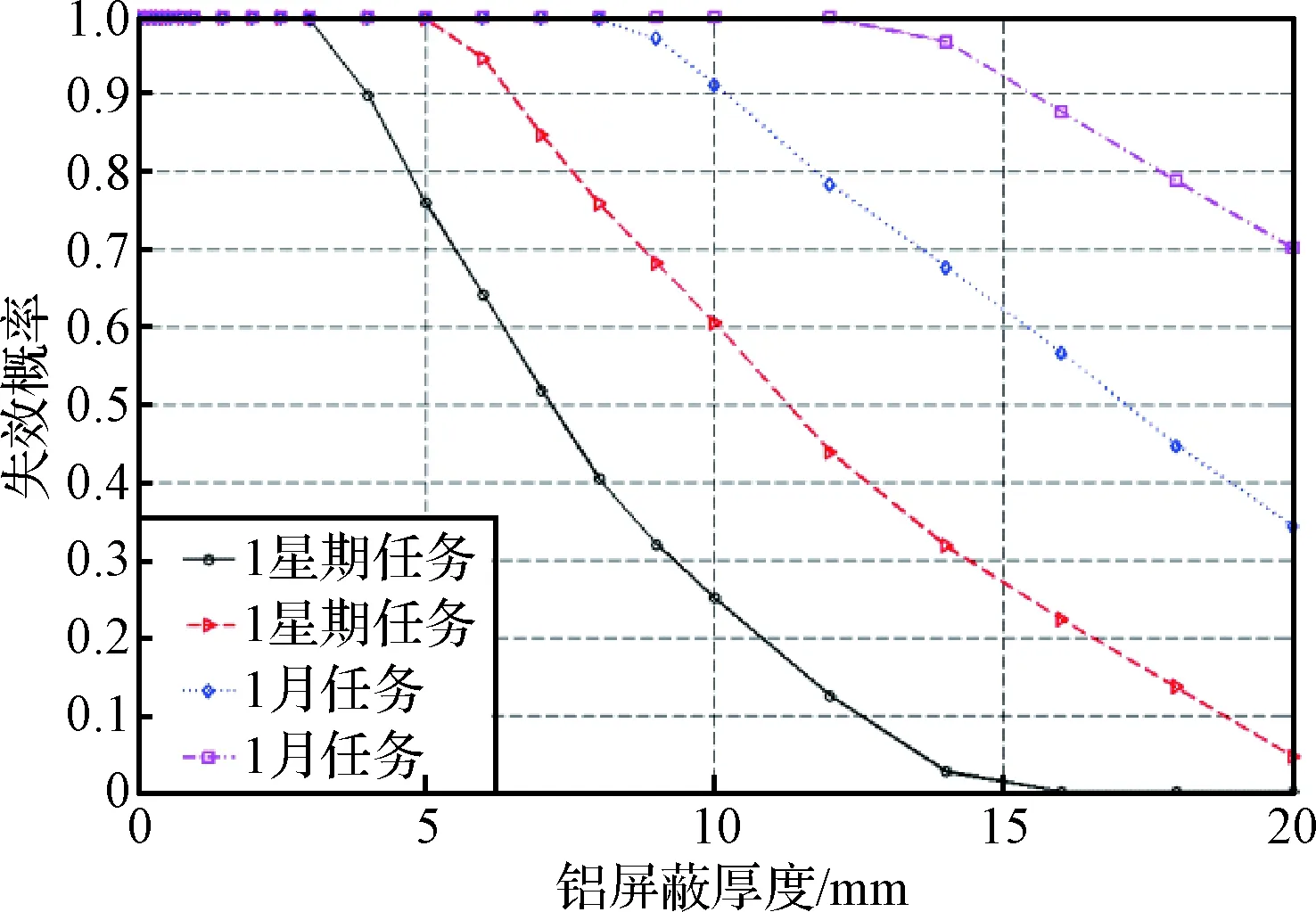
图8 不同任务期屏蔽厚度与失效概率的关系Fig.8 Relationships between shield thickness and failure probability for different missions

另外，计算了不同屏蔽厚度下，TL084器件存活概率随在轨时间的关系，如图9所示。定义器件存活概率为Ps，Guenther认为[26]存活概率随在轨时间指数衰减：Ps=exp(-at)，其中，a为失效速率。一般来说，随着在轨时间增加，器件存活概率快速减小，并缓慢达到完全失效(即存活概率为0)，从图中可知，对不同屏蔽厚度，失效速率不同。

进一步考察失效速率，假设存活概率存在如下形式并做拟合：

Ps=A×exp(-at) (ifPs<1)

(7)

式中：a为失效速率，A为常数。拟合结果如表4所示，失效速率随屏蔽厚度减小而增加，常数A随屏蔽厚度减小而缓慢增加。失效速率取决于剂量率，屏蔽厚度越小，器件所受辐射剂量率越大，失效速率越大。

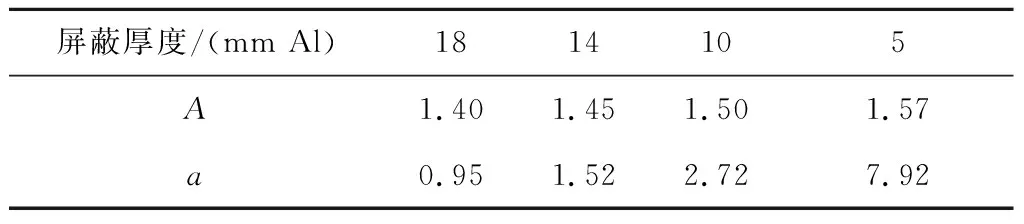
表4 不同屏蔽厚度存活概率拟合参数Table 4 The fitting parameters of survival probability after different shields

拟合结果基本与仿真结果相同，但在长时间和短时间时存在一定差异，因此详细考察不同在轨时段的失效速率a，以14 mm铝屏蔽为例，将在轨时间分为3段，分别进行拟合，结果如图10所示。随着在轨时间增加，器件所受剂量增加，失效速率a从1.36不断增加到2.50，而非在整个在轨期间保持不变。这是因为g(x)的偏度为负数，如图4(b)所示，相对而言，更高剂量下的器件失效率更大，即失效速率取决于器件失效剂量分布特征。因此，失效速率a受以下因素影响：辐射环境、器件辐照特性、屏蔽厚度、所受辐射剂量。失效速率随这些因素的改变而变化。

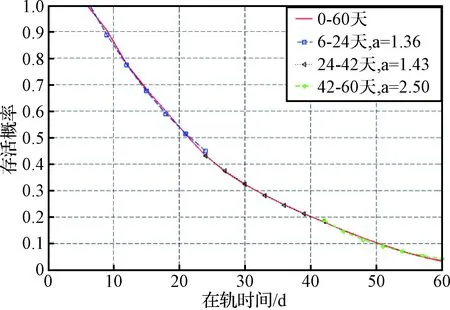
图10 14 mm铝屏蔽下在轨时间与存活概率的关系Fig.10 Relationships between on-orbit period and survival probability after 14 mm Al shielding

2.2 不同RDM下置信度分析

由于在工程设计中，RDM的应用有很长的历史，因此有必要评估本仿真方法和RDM的差别。假设RDM为1时置信度为50%，计算得到不同RDM对应的置信度，如图11所示。

设计中，通常选定某一RDM值，RDM越大对应的置信度越大，以1 mm铝屏蔽为例，其中RDM为2时对应置信度为0.89。当设计选取的RDM增加时，相应置信度的增加速度逐渐降低。另外，对于不同屏蔽厚度，RDM对应的置信度不同。RDM较小时，屏蔽厚度越大，置信度随RDM增加速率越大；RDM较大时，屏蔽厚度越大，置信度随RDM增加速率越小。如2.1节所述，这可能是由于木星中高能粒子通量不确定性小于低能粒子导致的，即相对而言，低能粒子更容易被扰动。因此，可根据本方法，在工程设计中，根据特定屏蔽厚度，选取最佳RDM，以达到最佳费效比。

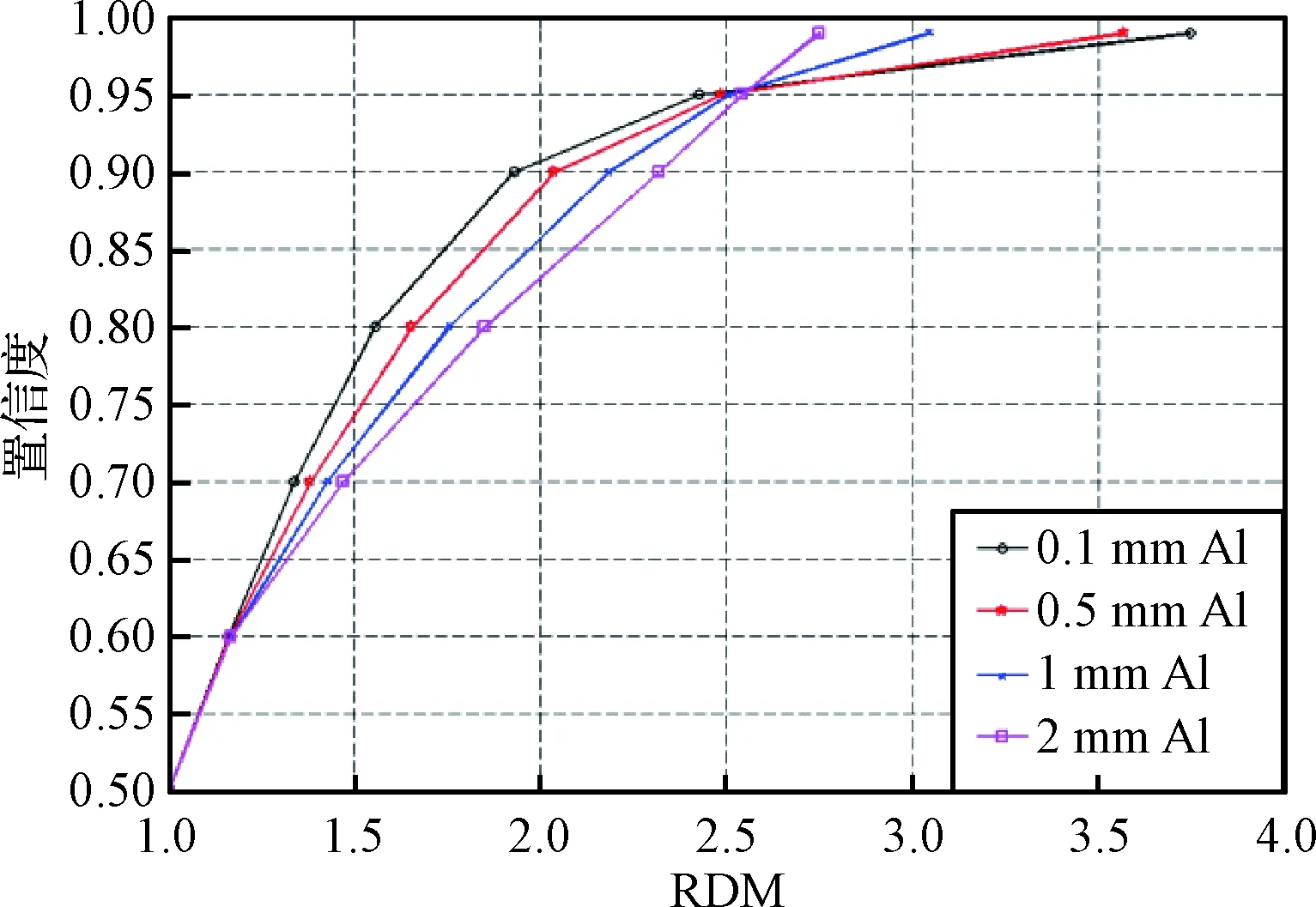
图11 铝屏蔽下不同RDM的置信度Fig.11 Confidence level of RDM after Al shielding

另外，考察了RDM和存活概率的关系，以10 mm铝屏蔽为例，如图12所示。根据不同RDM对应的置信度，得到对应RDM的辐射剂量。传统RDM设计中，认为器件达到RDM对应剂量，器件即失效，故在图中RDM对应存活概率为阶跃函数，器件只有存活和失效两种状态。而通过本文方法，可定量评估器件存活概率。对于TL084，由于器件对辐射敏感，RDM高估了在低剂量下的存活概率，而低估了在高剂量下的存活概率。如果以50%存活概率定义TL084的在轨存活时间，其寿命大于RDM为2.5的设计值，从而可达到优化设计的目的。

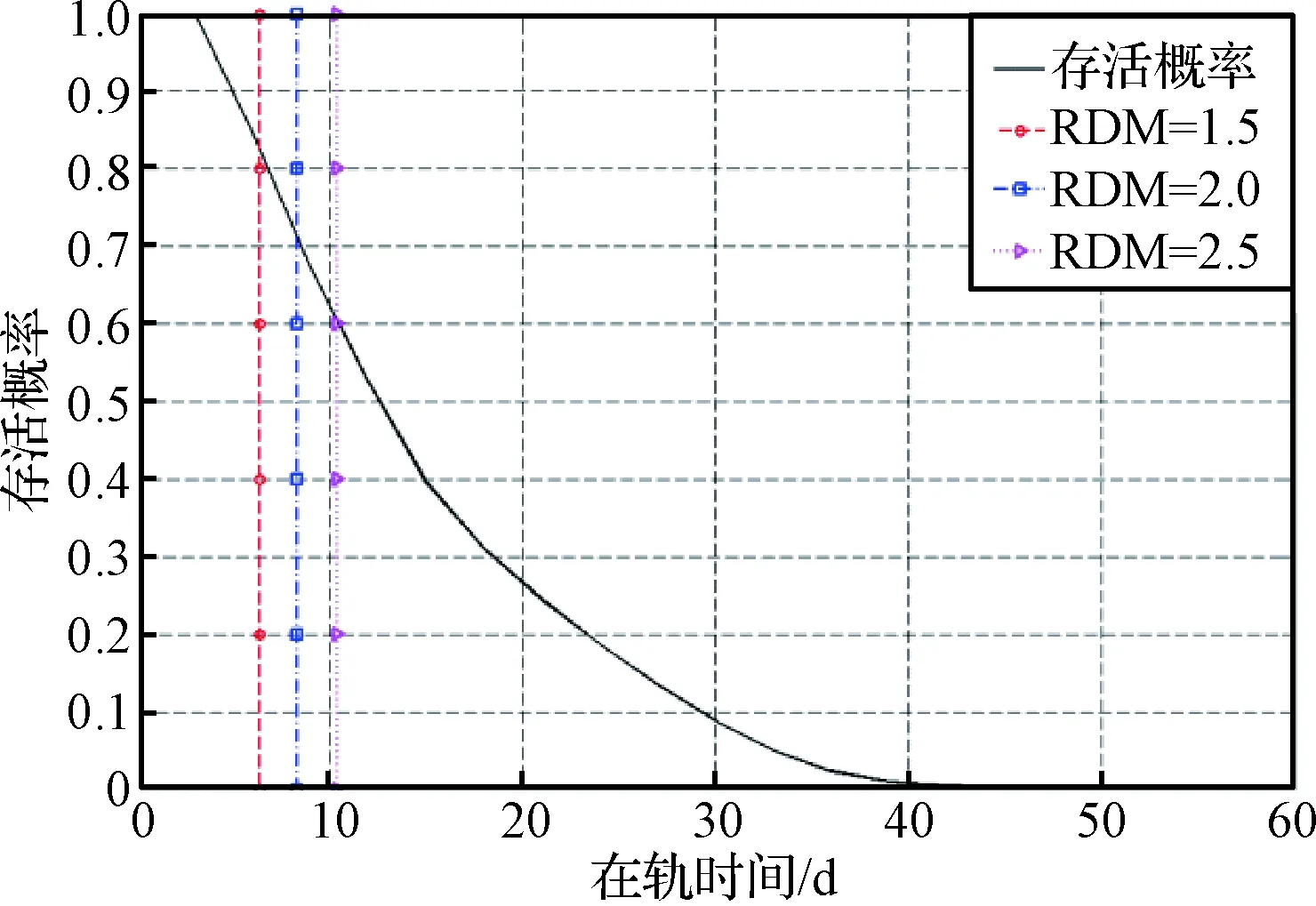
图12 10 mm铝屏蔽下RDM和存活概率的关系Fig.12 RDM vs. survival probability after 10 mm Al shielding

3 结束语

与地球相比，木星辐射环境十分恶劣，不仅粒子能量高、通量大，且辐射环境不确定性大。因此，辐射防护技术是木星系探测中的核心技术之一，其中总剂量效应需要重点考虑。传统基于平均辐射环境和器件平均失效剂量的RDM方法虽是行之有效风险控制方法，但在木星强辐射条件下，器件指标或屏蔽厚度难以满足设计要求，且无法定量评估元器件的失效概率，而使工程实现存在一定困难，需要更精确地评估器件对辐射剂量的响应。

本文将器件失效点剂量不确定性与辐射环境不确定性应用到总剂量评估中，解决了木星环绕任务总剂量设计的2个关键问题：一定轨道一定屏蔽下不同RDM设计值对应的置信度，以及具体元器件的失效概率及其随在轨时间的变化。利用此方法，可实现木星任务中器件指标、屏蔽厚度和失效概率之间的权衡和优化。该方法在满足以下条件时可很好地应用：1)器件对辐照剂量敏感；2)真实空间环境有不确定性；3)器件失效剂量不确定范围和在轨所受剂量不确定范围有一定重叠。

本文计算了假想任务中(10Rj×10Rj，0°)，不同屏蔽厚度和不同任务周期的TL084器件的剂量概率分布、失效概率、存活概率等参数。结果表明，在10 mm铝屏蔽下，TL084商业器件在轨正常运行时间一般不超过2星期。为了减缓总剂量导致器件失效的概率，需付出的屏蔽代价十分高昂。另外，随屏蔽厚度的减小，器件失效速率快速增加，随在轨时间的增加，器件失效速率缓慢增加。最后，考察了不同RDM值对应的置信度，对于1 mm铝屏蔽，RDM为2对应置信度89%。

木星探测辐射防护设计是复杂的系统工程，可在多个方面进行优化，如轨道优化、屏蔽材料优化、器件抗辐射加固等。结合本文方法，可定量考察这些因素对总电离剂量效应的影响。另外，本方法适用于器件失效剂量和空间环境剂量的不确定范围相近的情况，因此，除了强辐射的木星任务，该方法还可用于评估辐射敏感器件(耐辐射剂量性能低)在月球和火星探测任务(辐射剂量指标低)中的生存概率，以及在低成本卫星中辐射敏感器件的适用性。