运用推理方法 提升推理能力

胡新兰

摘 要：小学数学是小学唯一一门注重培养和发展学生抽象思维的学科。近年来，数学教育越来越重视学生思维能力的培养，要提高学生的思维能力，首先要改进学生的学习思维方式，逐步由外部知识向理性知识过渡，逐步由思维方式的转变向思维能力的提高过渡。

关键词：小学生数学;推理能力;教学策略

一、创设观察情境，培养观察能力

在通过推理解决问题的过程中，首先需要的是观察现有的事实，即找到已知的数学信息。小学生在解决问题的过程中可以完成单变量的数学推理问题，但如果对多变量的观察不够全面，则无法解决问题，原因是学生缺乏严谨全面的观察能力。在小学数学课堂上，需要调动学生积极观察和发现学科中的数学信息的能力，进而培养学生的推理能力是十分重要的。

1.多角度观测

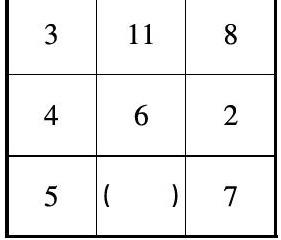
[例]根据规律，填写表格。

通过填写学生表格，充分体现了观察能力的重要性。当我们在日常数学课程中遇到这样的练习时，我们必须强调观察训练。在解释这个问题时，我们应该首先让学生找到问题中的数学信息。

“同学们，请告诉我，你在这个题目中看到了什么？”通过观察，学生不难看出表中有八个数字和一个空缺，但如果学生只给出这样的答案，则还需要进一步问：“这些数字是如何排列的？”它们分别在什么位置？学生会发现：从横向看，数字3、11和8之间的关系;4、6和2之间的关系;5、空格和7之间的关系。解决这个问题后，老师必须总结观察的方法：这9个数字纵、横、斜向排列，所以应该横向、垂直和斜向地观察它们。

2.掌握并观察有效信息

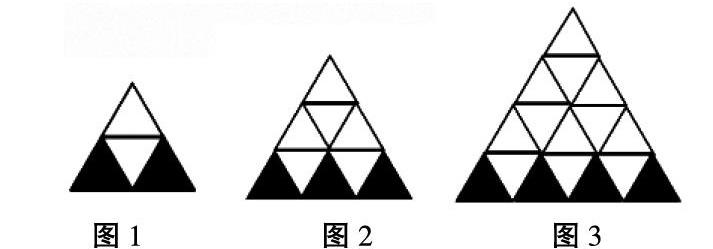
[例]找出规律。

题目：当大三角形底部有两个黑色小三角形时，整个图形需要多少个小三角形？当大三角形的底部有三个、四个、六个和n个小的黑色三角形时呢？

这个问题的第一个印象是关于这个题的信息很多，包括文本信息和图形信息，还有很多问题。在练习这些问题时，学生可以通过良好的训练来筛选有效的信息。

首先，给学生足够的时间观察主题，找出所有信息点。“请告诉我，你从题中知道了什么？”这是一个重要的链接。然后老师进行指导，“这个问题包含了很多信息，这些信息是否有助于我们解决问题，我们需要看问题是什么。”为了回答问题，第一个问题是“图1，底部有两个黑色三角形。整个图形需要多少个小三角形？”然后，“你在问题中发现了什么数学信息，请再说一遍？”通过一步一步的观察，学生很容易发现整个题唯一有效的信息是黑色三角形的数量和整个三角形的数量。我们需要做的是找出这两个数字之间的关系：2-4，3-9，4-16，6-36，n-nxn（或n2）。

二、培养外化思维，提高分析能力

马芯兰老师把问题解决的过程分为四个过程：阅读、画批、画图和说理。通过读、写、画、说，学生解决问题的困惑思维将成为一种外在表现。通过这种训练，可以有效地培养小学生思维的有序性和合理性，进而提高学生的思维能力和推理能力。

1.阅读题目

阅读题目是对题目进行考查，明确题的含义，对题目信息有初步的认知。这是解决任何问题的基础。在阅读问题的过程中，学生需要知道要解决的问题和相关信息，完成这一步骤有助于学生的分析和思考。

2.标记要点（画线）

标记的重点是掌握题目的关键信息或已有的事实，并加以标记，使其更为明显，更有利于学生对问题的认识和分析，适用于文本信息较多的问题，有很多方法可以标记重点，而绘制线条是最常用的方法。

3.画图

画图是用来分析数学问题中条件与问题之间的关系。绘图可以直观地显示题目的含义，系统地显示定量关系。小学生思维发展水平不够成熟。他们遇到一些抽象的、信息密集的、相对隐藏的数学问题。它们可以具体化抽象信息，帮助学生理清思路，找到解决方案。小学数学中常用的作图方法有线段图和几何图。

（1）线段图

线段图是由多个线段组成的平面图，用来表达定量关系，帮助人们分析和解决问题，它是小学数学学习和学生解题过程中最常用的图形，它主要用于份数问题和距离问题。

（2）几何图形

几何图形是小学数学课程学习中由正方形、矩形、三角形、梯形、多边形或不规则图形组成的平面图形，通过数字和图形的结合，帮助学生理解图形和几何知识，解决相应的实际问题。几何图形主要用于图形和几何的研究。

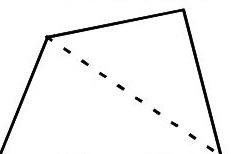
例如，已知，任意三角形的三内角之和是180度，那么，请计算出下面这个四边形的四个内角之和是多少？

解答这个题目时，已知信息是三角形内角和180度，所需求解的是四边形内角的总和。因为小学生还没有掌握四边形的内角之和，因此就需要利用已有的知识和经验，即已知的信息来解决这个问题，因此如何将四边形轉化为三角形是这个问题的关键。学生会想到把一个四边形分成两半，它会变成两个三角形。但在大脑中，在想象计算时很容易出错。此时，教师需要引导学生在纸上画出四边形，并将他们的思想具体化为真实的图形，然后很容易计算出四边形内角之和为180×2=360度。

4.解决问题

解决问题是实践正确的思想和方法，解决当前问题并取得一定成果的过程。这是学生整合信息、分析和综合的最后一步，如果之前所有的过程都被视为寻找钥匙，那么现在的过程就是打开门。

总之，通过合理推理能力的培养，学生可以改变思维方式，提高逻辑思维能力，从被动学习到主动学习，从被动接受学习到主动推理学习。面对更复杂的问题，他们不会等待别人的指导和帮助，他们会迅速了解问题的本质，系统而清晰地探索解决问题的途径，掌握学习的主动性。

编辑 鲁翠红