基于幂风险谱和蒙特卡洛模拟的贷款优化配置模型
2019-02-14迟国泰张亚京丁士杰
迟国泰,张亚京,丁士杰
(大连理工大学管理与经济学部,辽宁 大连 116024)
1 引言
贷款组合优化配置模型本质上是在综合考虑贷款收益和贷款风险条件下,求解一组恰当的贷款配置比例[1]。而商业银行中小概率的极端损失是不可避免的,因此研究考虑商业银行尾部风险的贷款配置问题具有重要意义。
在VaR风险测度方面,VaR (Value at Risk)是指在给定置信水平下贷款组合在一定时间内可能发生的最大损失[2]。刘艳萍等[3]通过约束贷款组合的VaR进行贷款配置。匡海波等[4]利用VaR建立了港口物流质押贷款组合模型。Lwin等[5]提出了MODE-GL演化算法求解均值-VaR的投资模型。
在CVaR风险测度方面,Artzner等[2]提出了CVaR(Conditional VaR)条件风险价值度量,CVaR是指资产组合损失大于给定VaR的条件下,资产组合的平均损失值,满足次可加性、凸性、一致性。Rockafellar和Uryasev[6]给出了将CVaR投资组合问题转化为线性规划模型求解的方法。Andersson等[7]以CVaR最小为目标函数进行资产配置。Alexander等[8]提出了一种基于平滑技术的方法实现CVaR的仿真。Najafi和Mushakhian[9]通过随机均值-半方差-CVaR方法构建了投资组合模型。Gao Jianjun等[10]通过LMP和CVaR建立了投资组合模型。
在谱风险测度方面的研究,Acerbi[11]提出了谱风险。Acerbi和Prospero[12]给出了谱风险在投资组合中的规划求解方式。Cotter和Dowd[13]比较了多种数值积分方法估算谱风险的精度。Adam等[14]对比了扭曲风险、谱风险在投资组合中的优劣。Lim[15]通过施加不同参数值的谱风险约束来解决误差敏感问题。韩萱和杨永愉[16]将风险厌恶系数与反映投资者心理的效用函数相结合构造了混合型谱风险。Abad和Iyengar[17]通过迭代梯度算法解决了多个谱风险约束的投资组合问题。刁训娣等[18]将极值理论与谱风险测度方法相结合进行资产配置。
在蒙特卡洛模拟应用于资产配置方面,历史数据往往较少或者较难获得,不足以可靠地估计贷款可能造成的风险,因此许多研究采用蒙特卡洛方法进行贷款收益或损失的模拟与仿真。马志卫和刘应宗[19]将贷款看做投资项目,以投资项目的财务内部收益率和波动反映贷款收益和风险,并以蒙特卡洛进行收益模拟,结合无差异曲线与有效前沿进行贷款配置。司继文等[20]通过蒙特卡洛模生成股票收益情景,并利用CVaR和混合整数规划进行贷款配置。
上述研究不足在于:一是VaR仅将信用风险转化为单一分位点,但也因此不能充分考虑超出分位点的下方风险值分布;CVaR同等看待尾部风险的大小,并没有给不同损失赋以不同厌恶权重。二是现有谱风险研究并没有将谱风险与贷款信用风险相结合,仅单一考虑了尾部风险,没有兼顾信用风险。
针对上述存在问题,本文建立了基于幂风险谱和蒙特卡洛模拟的贷款优化配置模型。本文根据贷款组合尾部损失越大、对应风险厌恶权重也应越大的思路,通过幂风险谱对极端风险进行控制,即弥补了CVaR仅均等看待尾部风险、忽略风险较大的损失应予以更大权重,也同时弥补VaR仅提供某一置信水平下资产损失的最大值、无法反映超过阈值的损失的弊端。
2 科学问题的提出及难点
2.1 商业银行贷款配置的特点
(1)商业银行贷款配置面临风险是不可避免的,如果仅约束贷款组合的发生概率,而不控制极端风险出现时的损失大小,则极易出现“黑天鹅”事件。若银行在99%的置信水平下发生1000万损失的概率是1%,显然对银行影响不大;但若在万分之一的小概率下发生500亿损失,则银行的生存就可能有问题。前者是“概率大小”问题;而后者则讲的是“损失大小”问题。显见,损失大小的“黑天鹅”事件,才是银行应该重点控制的问题。
(2)贷款配置时,信用等级变化引起的风险常常被忽略,且由于贷款历史数据较少,往往无法获得贷款客户的历史损失分布,造成贷款配置时很少考虑信用等级变化的风险。
2.2 问题的难点
难点1:用何种方法度量贷款组合的尾部风险,避免资产配置的“黑天鹅”事件发生。尾部风险出现概率虽小,但是一旦发生,对于银行将产生极端的损失。恰当的风险度量方法是商业银行在贷款配置过程中不可或缺的风险防范手段。
难点2:如何将信用等级变化引起的风险纳入总体风险的度量?信用等级的微小变化就会引起的总体风险变化,准确度量信用等级改变引起的风险对于银行风险控制极为重要。
2.3 突破问题的思路
思路1:根据贷款组合尾部损失越大、对应风险厌恶权重也应越大的思路,通过幂风险谱对极端风险进行控制,即弥补了CVaR仅均等看待尾部风险、忽略风险较大的损失应予以更大权重,也同时弥补VaR仅提供某一置信水平下资产损失的最大值、无法反映超过阈值的可能损失的弊端。
思路2:通过蒙特卡洛模拟信用等级迁移引起贷款收益的变化情景,将信用迁移引起的风险引入风险度量中,弥补了现有研究仅考虑违约风险忽视信用等级变化的不足,并解决贷款历史数据不足的问题。
3 贷款组合优化模型的建立
3.1 幂风险谱测度
3.1.1 风险价值VaR
VaR(Value at Risk)是指在一定置信水平1-α下,某金融资产组合在将来的一段时间内可能的最大损失。利用公式表示为[11]:
P(X<-VaRα)=α
(1)
令贷款组合收益率X的累积分布函数为F(x),则可将式(1)转化为[11]:
(2)

3.1.2 条件风险价值CVaR
条件风险价值CVaR是指在一定置信水平1-α下,某金融资产组合在未来一段时间内损失超过VaR的平均值,利用公式表示为[14]:
(3)
式(3)中CVaR指在1-α置信水平下贷款组合损失大于VaRα的全部损失值的算数平均值。
3.1.3 谱风险测度
(1)连续形式的谱风险
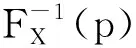
(4)

在式(4)中的风险厌恶函数φ(p)是p∈[0,1]上的可积函数。且φ(p)满足非负、正则、弱递减性[21]:
(i)φ(p)≥0,∀p,非负性。

(iii)φ(p1)≥φ(p2),ifp1≤p2,弱递减性。
式(4)中φ(p)是风险厌恶函数,从条件(iii)知p1≤p2时,φ(p1)≥φ(p2),故φ(p)为单调递减的。

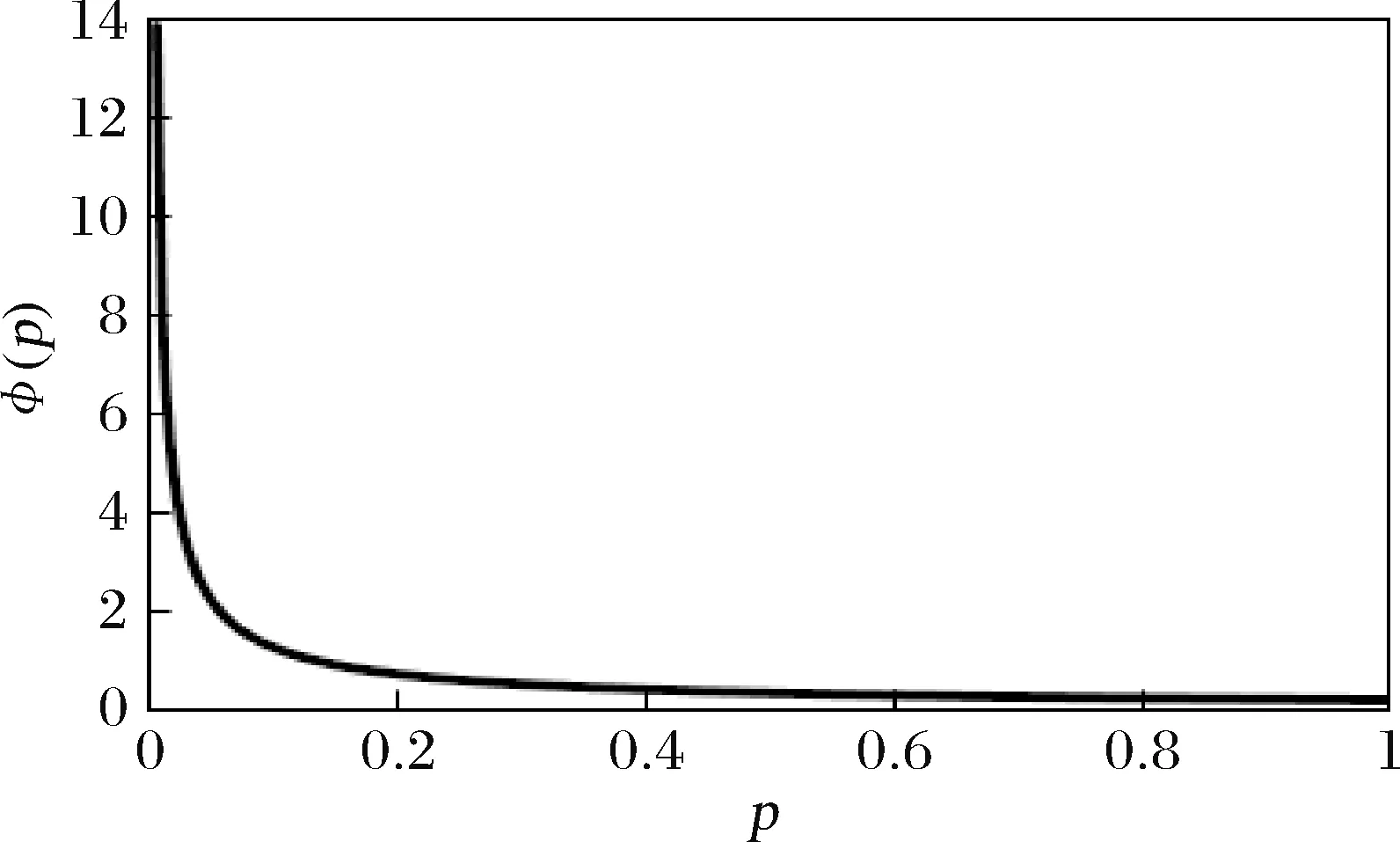
图1 谱风险测度的风险厌恶权重
(2)离散形式谱风险
很多情况下资产分布F(x)并不是确定的,是根据历史资产收益进行计算谱风险,此时使用到谱风险的离散形式,将式(4)转化为离散形式如下[8]:
(5)
其中,N为有N种情景。
①式(5)中φi:为风险厌恶函数φ(p)的离散形式,通过积分表达后为[8]:
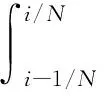
(6)
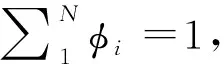
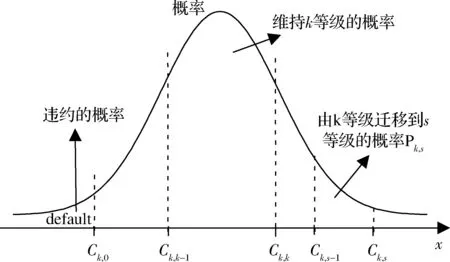
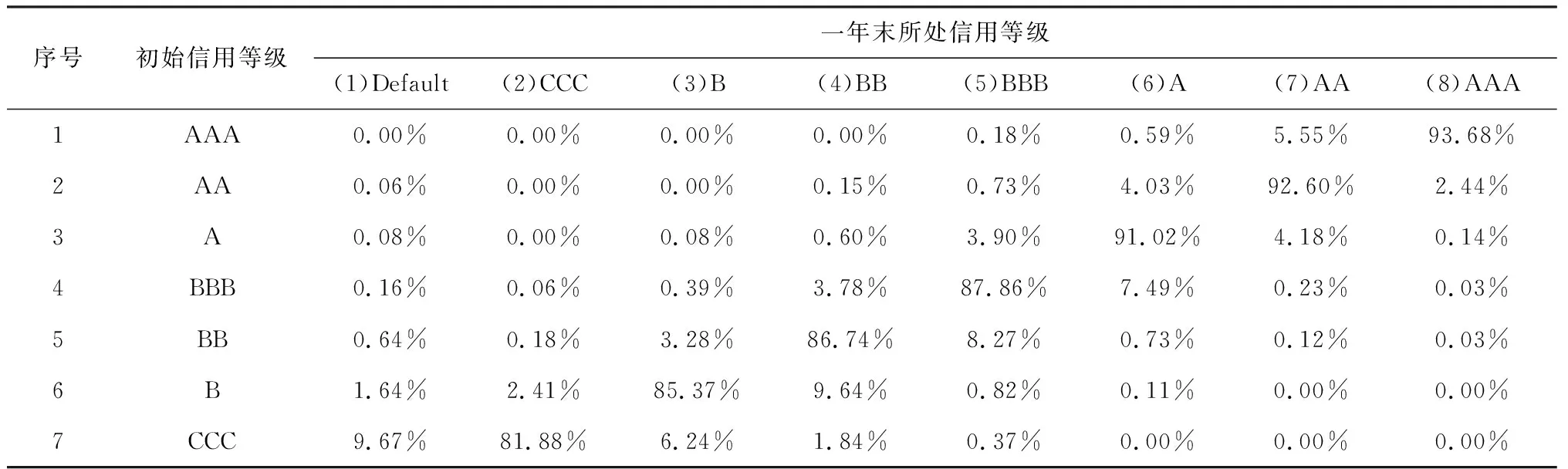
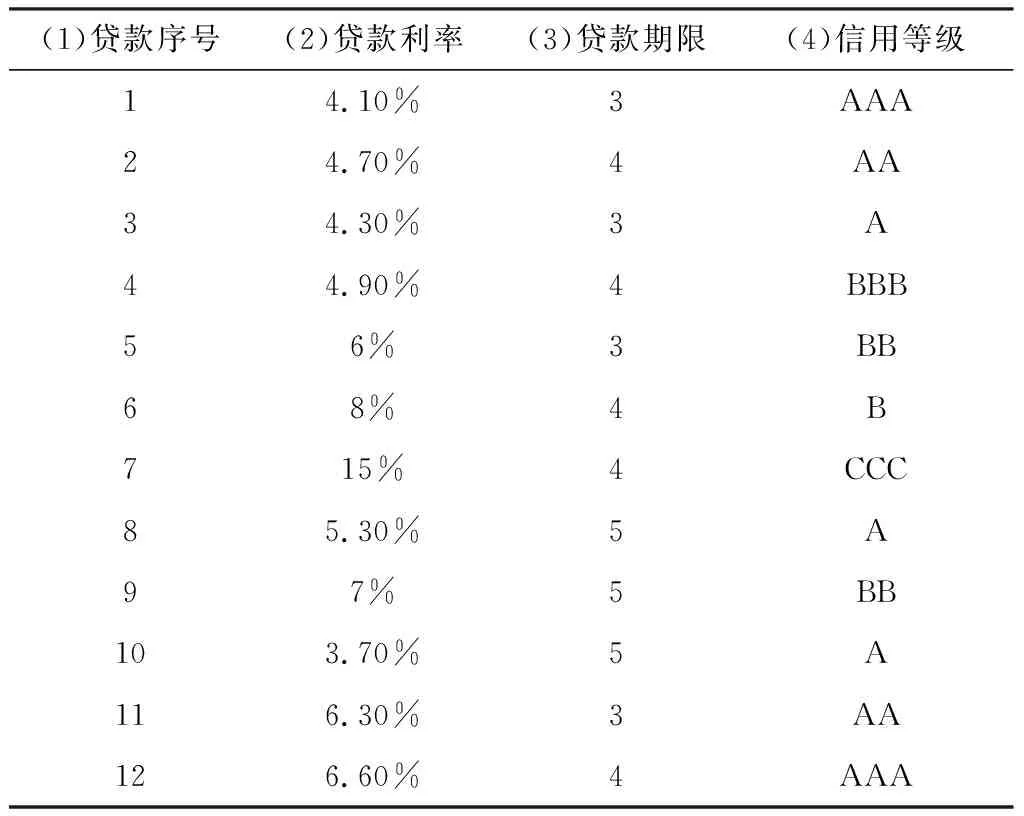
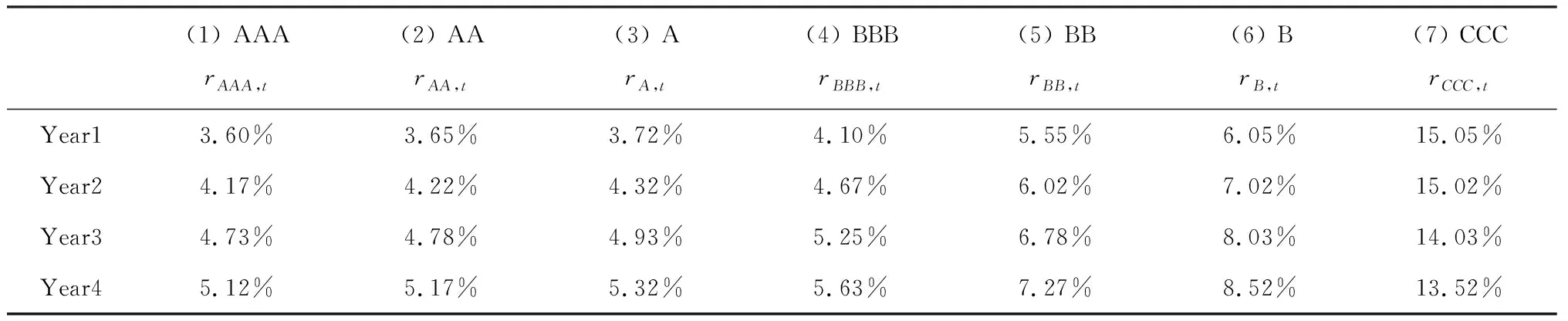
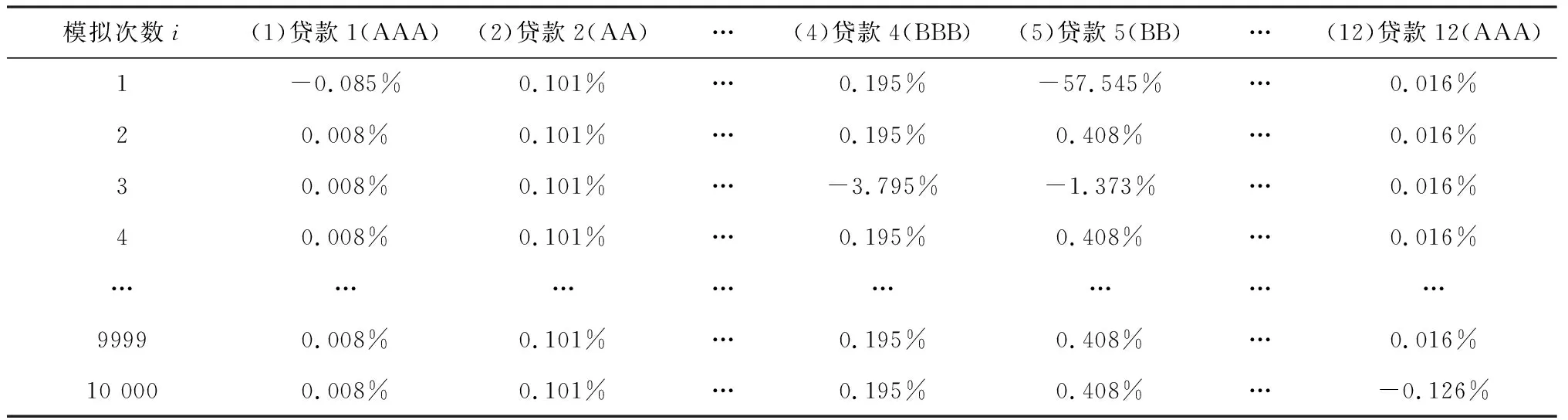
②式(5)中Xi:N:Xi:N是个有序变量,为N个收益由小到大排列后的第i个收益。{Xi:N|i=1,…,N}={Xi|i=1,2,…,N},并且Xi:N 式(5)的含义:式(5)中的收益Xi:N是由小到大排列的,即将损失-Xi:N由大到小排列。而式(5)中的风险权重φi是由大到小排列的。即对较大的损失-Xi:N,赋予较大的风险权重φi,反映了对风险的厌恶偏好。 (3)幂风险谱PSR (Power Spectral Risk) 令式(4)中的φ(p)为幂函数[18]: φ(p)=(1-β)p-β,(0<β<1) (7) 其中,β为绝对风险厌恶系数,根据金融机构自己风险厌恶程度自行在0-1之间取值[18]。β越大代表对尾部风险厌恶程度越大,由图2可知,β=0.8对应的φ(p)曲线中尾部风险厌恶程度大于β=0.5时的风险厌恶程度。 图2 幂风险谱测的风险权重 (8) 将式(8)代入式(5),得到幂风险谱测度PSR[18]: (9) 因此幂风险谱式(9)既弥补了下文式(14)风险价值VaR[2-5]仅考虑了一个点的损失,即某一置信水平下资产损失的最大值-XNα:N、无法反映一旦超过这一数值的可能损失的弊端。又弥补了下文式(17)中条件风险价值CVaR[6-9]同等看待尾部风险,即相当于对尾部风险均赋予同等权重φi=1/Nα,忽略风险较大的损失应予以更大权重的不足。 3.2.1 VaR与CVaR是连续型谱风险式(4)的特例 (1)风险价值VaR是本文连续型谱风险式(4)的一个特殊情况。 设:δ为脉冲响应函数(Dirac-delta狄利克雷函数),则风险价值VaR对应的风险权重φ(p)[18]: (10) 式(10)赋予尾部概率p=α时对应的损失额无穷大的权重,而其余收益分位点上的权重为0。即风险价值VaR对应的φ(p)仅在α分位点对应一个风险数值,其他分位点的风险没有考虑。 (11) 故,式(2)的VaR即为本文式(4)的一个特例。 本文式(4)的谱风险Mφ与式(2)的风险价值VaR的区别至少有二: 二是对待风险大小的态度不同。风险价值VaR无论风险大小,都是一个常数VaRα。而对于本文式(4)的谱风险Mφ,它对较大损失赋予越大权重φ(p),因此谱风险是反映风险厌恶偏好的风险测度指标。 (2)条件风险价值CVaR是本文连续型谱风险式(4)的一个特殊情况。 设:φ(p)-风险权重,有[18]: (12) 其中I为示性函数,当p≤α时,I=1,否则为I=0。 式(12)的CVaR对应的风险权重φ(p),在p≤α时,表示CVaR对0~α分位点的损失赋予的权重均为1/α。没考虑损失越大、厌恶权重越大,赋予同等权重,没反映风险偏好。在p>α时,表示CVaR对于α~1分位点的损失赋予的权重均为0。没考虑α~1分位点的损失较小的情况。 将式(12)的两种表现形式代入式(4),则[18]: (13) 因此得到式(13)的CVaR,也就是得到了上文式(3)中的CVaR。故CVaR即为本文式(4)的一个特例。 本文式(4)的谱风险Mφ与式(3)的条件风险价值CVaR的区别至少有二: 一是测度风险区间不同。CVaR是对p∈[0,α]分位点对应的风险。而本文式(4)中对应的谱风险Mφ是p∈[0, 1]全部分位点对应的风险。二是对待风险大小的态度不同。CVaR无论尾部损失大小,对于p∈[0,α]对应的损失,赋予的权重均为1/α。而对于本文式(4)的谱风险Mφ,它对较大损失赋予越大权重φ(p),反映了风险厌恶的偏好。 综合上述,本研究用反映损失越大、风险权重越大的式(4)谱风险Mφ来度量风险,改变了条件风险价值CVaR对于损失超出阈值部分的风险权重为同一定值,并没有体现出商业银行对于银行风险越极端、厌恶程度越高、控制力度越大的不足。 3.2.2 VaR与CVaR是离散型谱风险式(5)的特例 (1)离散形式的风险价值VaR式(14)是离散形式谱风险式(5)的特例。 VaRα=-Xn:N=-XN·α:N (14) 当置信水平1-α=95%,模拟次数N=10,000时,则n=N·α=10,000×5%=500,风险价值VaRα的值即为贷款组合收益Xi由小到大排序,即损失-Xi由大到小排序后,在第500位的那一个损失-X500:10 000。 (15) 将式(15)中两种情况下的φi代入式(5),并注意到式(14)中的VaR,则: (16) 因此,离散型风险价值VaR式(14)即为本文离散型谱风险式(5)中的一个特例。 上文幂风险谱的式(9)弥补了式(14)风险价值VaR仅考虑了一个点的损失,即某一置信水平下资产损失的最大值、无法反映一旦超过这一数值的可能损失的弊端。式(9)中幂风险谱考虑了多个点的损失,且对于较大的损失-Xi:N赋予较大的风险权重φi,反映了对风险的厌恶偏好。 (2)离散形式条件风险价值CVaR式(17)是离散形式谱风险式(5)的特例。 设:CVaRα-置信水平取1-α时的条件风险价值,E(·)-期望函数,X-贷款收益,VaRα-置信水平取1-α时的风险价值,N-模拟总次数,Xi:N-资产收益X由小到大排列后的第i个资产收益,则[13]: (17) 式(17)的含义:在由小到大排列后Nα个资产组合收益进行算术平均计算,即为条件风险价值CVaR。 将式(12)代入式(6),得到条件风险价值CVaR离散形式的权重φi[13]: (18) 式(18)中字母与式(6)、式(12)中含义相同。 将式(18)中两种情况下的φi代入式(5),并注意到式(17)中的CVaRα,则[13]: (19) 因此,离散型条件风险价值CVaR为离散型谱风险式(5)中的一个特例。 上文幂风险谱式(9)弥补了条件风险价值CVaR式(17)对尾部风险均赋予同等权重φi=1/Nα,忽略风险较大的损失应予以更大权重的不足。式(9)中幂风险谱对较大损失-Xi:N,赋予较大权重φi,反映了对风险的厌恶偏好。 用Monte Carlo模拟信用等级迁移引起贷款收益的变化情景,将信用等级变化引起的风险引入风险度量中,解决贷款历史数据不足的问题。 3.3.1 贷款收益率 设:ri-第i笔贷款信用等级变为Si时(Si为非违约级别)的贷款收益率;pi-一年后的利息;Ti-第i笔贷款的贷款期限;rSi,t-信用等级为Si的贷款第t年的远期利率(见表4)。则[22]: (20) 式(20)考虑一年后信用等级变化情况[22],考察时间点为一年末,信用等级在一年末一旦发生迁移,就按照迁移后的信用等级对应的零息票收益曲线中的远期利率进行折现,通过式(20)反映信用等级迁移对贷款收益率的影响。 若一年后等级Si为违约级别时,通过下文式(21)求贷款收益率。设:ri-贷款收益率,di-违约时的挽回率,则[22]: ri=di-1 (21) 其中,一笔贷款违约时的挽回率di在模拟过程中,通过在满足贝塔分布β(a,b)的数中随机产生,其中a,b为决定贝塔分布均值和方差的相关参数[22],下文实证4.2中参照现有研究[22]选取贝塔分布的参数为β(a,b)=β(2,8)。 3.3.2 信用等级迁移 根据CreditMetrics框架[23],可知一个企业贷款从初始信用等级K级,迁移到S级的概率分布服从标准正态分布N(0,1),如图3[23]所示。信用等级从低等级到高等级排列后为违约Defualt(1)、CCC(2)、B(3)、BB(4)、BBB(5)、A(6)、AA(7)、AAA(8)个等级。 图3 贷款收益与信用等级之间的关系[23] 设:Pk,s-贷款信用等级从k级转移到s级的概率,Φ(·)-标准正态分布的累积概率分布函数,Ck,s-信用等级从k级迁移到s级的临界点,x-模拟时随机产生的标准贷款收益率,则[23]: Pk,s=Φ(Ck,s-1 (22) (23) 式(22)为贷款从k等级转移到s等级的概率Pk,s。当随机生成的标准贷款收益率x处于Ck,s-1 由此将下文3.3.3中每个模拟出的贷款收益x,与信用等级转移临界点Ck,s进行对比,便可知企业一年后的信用等级。 以BBB级为例,说明信用等级迁移临界点Ck,s确定的过程。 表1是信用等级迁移矩阵[23],如表1第4行是BBB级客户迁移分别到Default级、CCC级、…、AAA级的概率,为0.16%、0.06%、…、0.03%。 将表1第4行第1列BBB级迁移到违约的概率PBBB,1=0.16%代入式(23)并查正态分布表,可得BBB级迁移到违约Default(1)级的临界点CBBB,1: CBBB,1=Φ-1(PBBB,1)=Φ-1(0.16%)=-2.945。 将结果列入表2第4行第1列。 …,…,… BBB级迁移到AA(7)的临界点CBBB,7: CBBB,7=Φ-1(PBBB,1+PBBB,2+…+PBBB,7)=Φ-1(0.16%+0.06%+…+0.23%)=Φ-1(99.97%)=3.412 表1 一年内信用等级转移矩阵[23] 表2 信用等级迁移临界点Ck,s BBB迁移到各等级的临界点如表2第4行所示。同理,可得AAA、AA、…、CCC等级向其他等级迁移的临界点Ck,s,如表2其他行所示。 3.3.3 贷款收益率的Monte Carlo模拟 步骤1:随机生成一组符合m维正态分布N(0,Cov)的向量x=(x1,…,xm)T,代表m笔贷款的标准收益率。 步骤2:根据贷款i的初始信用等级,将步骤1中得到的每一个贷款收益xi分别与表2其初始信用等级所在行的等级迁移临界点Ck,s进行比较,如初始等级为BBB级,则与表2中BBB级所在行第4行进行比较。当第i个贷款收益xi满足关系Cki,si-1 步骤3:计算信用等级迁移后的贷款收益r。 ①当迁移后等级si为非违约等级,则由式(20)可以计算一年末的收益率。②当迁移后等级si为违约等级,则通过式(21)计算贷款收益率。由此,模拟出m笔贷款一年后经过信用等级迁移后的收益率值r1j=(r11,…,r1m),得到第一次模拟情景的值。 步骤4:重复N次步骤1-步骤3,可模拟出m笔贷款的N种不同情景下的收益值,即:rij=(ri1,ri2,…,rim),i=1,…,N。 步骤5:计算每笔贷款N种情景下收益率的均值uj。 设:uj-第j笔贷款全部N种情景模拟的收益率均值,N-模拟总次数,rij-第i种情景模拟出的第j笔贷款收益率,m-贷款笔数。则[22]: (24) 步骤6:确定信用迁移后的收益率的变化量Xij。 设:Xij-第i种情景第j笔贷款信用等级迁移后引起的收益率变化量,则[22]: Xij=rij-uj (25) 式(25)通过信用等级迁移后贷款收益率rij与收益率均值uj之间的差值Xij,反映信用等级迁移引起的贷款收益变化。 3.4.1 目标函数中的主要参数 设:Xi-第i种情景信用等级迁移引起的贷款组合收益变化量,wj-第j笔贷款配置比例。则[22]: (26) 式(26)的含义:通过上文式(25)中得到的第i种情景第j笔贷款信用等级迁移后收益率变化量Xij,乘以对应贷款配置权重wj,确定信用风险迁移后第i个情景下的贷款组合收益的变化量Xi。当Xi>0,表示情景i的贷款组合收益因信用等级迁移产生了收益。反之,表示因信用迁移产生了损失。 其中,下文式(27)中的Xi:N即为式(26)中所得的收益率变化量Xi由小到大排序后所得值。 式(26)中的rij为信用等级迁移后的贷款利率,通过式(26)将信用等级迁移的风险纳入总体风险度量体系之中,从而在总体上对信用风险的不确定性有了较可靠的把握。完善了现有研究中常常忽略信用等级变化风险的不足。 3.4.2 目标函数的确定 以上文式(9)的贷款组合收益的幂风险谱MPSR最小为目标,建立目标函数如下[18]: (27) 式(27)目标函数的好处:根据给不同贷款组合损失-Xi越大,其风险权重φi也就越大的思路,构建幂风险谱MPSR最小建立非线性规划的目标函数,使资产配置的最优组合反映的风险厌恶的价值偏好。即弥补了现有研究条件风险价值CVaR[6-9]仅均等看待尾部风险、忽略风险较大的损失应予以更大权重,也同时弥补了现有研究风险价值VaR[2-5]仅提供某一置信水平下资产损失的最大值、无法反映一旦超过这一数值的可能损失的弊端。 3.4.3 约束条件的确定 (1)贷款组合收益大于给定目标收益。 设:u-贷款组合收益,m-贷款个数,uj-第j笔贷款N种情景模拟的收益率均值,wj-第j笔贷款的配置权重,r0-给定目标收益,则[22]: (28) (2)权重加和为1。 设:m-贷款个数,wj-贷款的配置权重,则[22]: (29) (3)风险集中度约束 设:wj-第j笔贷款的配置权重,则[22]: 0 (30) 式(30)的含义:通过单个资产权重wj小于20%[22],避免资产过于集中[22]。 以式(27)为目标函数,以式(28)-式(30)为约束,构建基于幂风险谱的贷款优化配置模型。 特点:通过蒙特卡洛模拟信用等级迁移引起贷款收益的变化量Xi。并以信用等级迁移后贷款组合损失越大、则风险厌恶权重越大的思路构建式(27)的幂风险谱PSR最小为目标函数,以贷款组合的收益大于目标收益为约束,构建贷款优化配置模型,同时控制信用风险和尾部极端风险。 本文待配置贷款共有12笔,12笔贷款信息如表3所示远期利率[23]。表5前10行收集了某银行十年间,与12笔贷款同信用等级、同贷款年限的实际收益率历史数据。 表3 贷款信息 表4 不同信用等级远期利率(零息票曲线对应利率)rSi,t[23] 表5 全部贷款的历史收益率hti(%) (1)Monte Carlo模拟收益率 步骤1:确定12笔贷款的相关系数矩阵。 (31) 将表5数据代入式(31)得到贷款之间的相关系数,结果如表6所示。用矩阵ρ的形式表示: (32) 表6 各企业贷款收益率之间的相关系数矩阵ρ=[ρij]m×m 步骤2:随机生成一组12笔贷款的标准收益率。 令贷款1、…、贷款12的贷款收益率随机变量分别记为x1、…、x12,且分别服从标准正态分布,x1~N(0,1),…,x12~N(0,1)。 12个贷款的标准化收益率的联合分布(x1,x2, …,x12)服从12维的正态分布N(0,Cov)。 其中,12维正态分布N(0,Cov)中0=(0,0,…0)12×1,Cov为12笔贷款的协方差矩阵。12笔贷款的协方差矩阵Cov为式(32)所得相关系数矩阵。 由Matlab软件中的函数mvnrnd(μ,Cov)可随机生成服从12维正态分布N(0,Cov)的收益率。第一次随机生成的12笔贷款的收益率向量为x=(x1,…,x12)T=(-1.601, …, -1.438)T,结果列入表7第1行。 重复本步骤步骤2可以得到表7第2-10000行。 表7 Monte Carlo模拟得到的不同贷款标准化收益率x 步骤3:将步骤2中随机生成的标准化收益率分别与表2中信用等级迁移临界点Ck,s进行对照,确定12笔贷款其一年后的信用等级。结果列入表8。 步骤4:信用等级迁移后的贷款收益率的确定。 第1次模拟贷款1时,将贷款利率p1=4.10%、贷款期限T1=3、AA级1年后的远期利率rAA,1=3.65%、AA级2年后的远期利率rAA,2=4.22%代入式(20),则第1次模拟的贷款1的等级迁移后的利率r1,1=3.896%,列入表9第1行第1列。 同理可得剩余11笔贷款信用等级迁移后的收益率,如表9第1行第2-12列所示。 表8 Monte Carlo模拟第一年末时贷款信用等级S 表9 Monte Carlo模拟第一年末时贷款收益rij 表10 信用等级迁移引起的收益变化量Xij a)重复本步骤步骤4可以得到表9第2-10000行。 应该指出,若信用等级迁移后变为“违约”等级,则根据式(21)计算收益率。 (2)信用等级迁移后贷款收益的变化量Xij。 ①确定每笔贷款在10000种情景收益率的均值uj。将表9第1列前10000行代入式(24):u1=(3.896%+…+3.99%)/10000=3.981%。结果列入表9最后一行第1列所示。 同理可以得到其他11笔贷款的收益率均值uj,如表9最后一行第2-12列所示。 ②信用等级迁移引起的收益率变化量Xij。将表9第1行第1列r1,1=3.896%、及最后1列u1=3.981%代入式(25):X1,1= 3.896%-3.981%= -0.085%。结果如表10第1行第1列。得到第1种情景中贷款1因信用等级迁移引起的收益率变化量X1,1= -0.085%<0,表明信用等级迁移后引起损失,表明贷款1信用等级由AAA级迁移到AA级引起损失。 同理可得其他情景中每笔贷款因信用等级迁移引起的收益率变化量Xij,如表10其他行列所示。 4.3.1 目标函数的确定 (1)信用等级迁移后贷款组合收益变化量Xi。 将表10中的信用等级迁移引起的贷款收益变化量Xij逐行分别代入式(26)中,可得到每一次模拟因信用等级迁移引起总变化量表达式Xi: (33) 其中,w=(w1,w2,…,w12)表示组合中12笔贷款的配置比例,为待求解变量。 虽然式(33)中的X1,…,X10000含有未知变量wj,但在求解过程中每次给定一组wj,即可确定出式(33)的Xi,将式得到X1,…,X10000由小到大排列后对应的值即为目标函数式(34)中X1:10000,…,X10000:10000。直至式(34)最小时,得到最终的贷款配置比例wj。 因此、下文式(34)中X1:10000,X2:10000,…,X10000:10000是式(33)得到Xi由小到大排列后对应的值。 (2)幂风险谱的风险厌恶权重φi。 通过式(8)确定10000种情景贷款组合收益排序后对应的风险厌恶权重φi,i=1, …,10000。 同理可得φ2,…,φ10000,结果如表11第1行第2-10000列所示。 (3)基于幂风险谱最小的目标函数。 将表11中风险厌恶权重φi代入式(27): =-(0.01X1:10000+…+0.000050X10000:10000) (34) 式(34)根据“不同贷款组合的损失-Xi越大,其风险权重φi越大”的思路,以幂风险谱MPSR最小建立非线性规划模型,使资产配置的最优组合反映的风险厌恶的价值偏好。 4.3.2 约束条件的确定 约束1:贷款组合收益大于给定目标值r0。 将表9最后一行uj值,代入式(28)不等号右侧,得到贷款组合收益: u=3.981%w1+4.475%w2+…+11.836%w12 (35) 再将给定目标收益r0=6.5%[19],代入式(28): 3.981%w1+4.475%w2+…+11.836%w12≥r0=6.5% (36) 约束2:贷款配置比例wj加和为1。根据式(29): w1+w2+…+w12=1 (37) 约束3:单笔贷款权重wj小于等于20%[19]。 0 (38) 4.3.3 模型的求解 以式(34)为目标函数,以式(36)-(38)为约束,构建基于幂风险谱PSR最小的贷款组合优化模型,通过非线性规划求解最优资产配置比例w。 求解过程由Matlab实现,求解的贷款配置结果wj如表12第1行前12列所示。 将表12第1行第1-12列代入式(35)得到贷款组合收益0.068,结果列入表12第1行第13列。 将表12第1行第1-12列代入式(33)后求得10000个Xi,将Xi由小到大排序后代入式(34)可求得幂风险谱为0.0101,结果列入表12第1行第14列。 将表12第1行第13、14列,代入“收益/幂风险谱”=0.068/0.101=6.73,表示单位幂风险谱上获得的收益,结果列入表12第1行第15列。 思路:将式(34)中目标函数替换为式(21)的贷款组合收益的风险价值VaR最小,其他约束条件式(36)-(38)不变,构建对比模型1。求解所得贷款配置结果如表12第2行前12列所示。 表11 幂风险谱的风险厌恶权重φi 表12 贷款配置结果 将表12第2行第1-12列代入式(35)得贷款组合收益0.0675,结果列入表12第2行第13列。 将表12第2行第1-12列代入式(33)后求得10000个Xi,将Xi由小到大排序后代入式(34)可求得幂风险谱为0.0197,结果列入表12第2行第14列。 将表12第2行第13、14列,代入“收益/幂风险谱”=0.0675/0.0197=3.43,表示单位幂风险谱上获得的收益,结果列入表12第2行第15列。 思路:将式(34)中目标函数替换为贷款组合收益的条件风险价值CVaR式(27)最小,其他约束条件式(36)-(38)不变,构建对比模型2。求解所得贷款配置结果如表12第3行前12列所示。 与上文5.1同理求得贷款组合收益0.0693、幂风险谱为0.0129、“收益/幂风险谱”=0.0693/0.0129=5.37,结果列入表12第3行第13-15列。 由表12可知,表12第1行第1-12列是本模型对于12笔贷款的配置结果,表12第2行是对比模型1用VaR最小为目标函数的贷款配置结果,表12第3行是对比模型2用CVaR最小为目标函数的贷款配置结果。 收益方面,由表12第12列可知,是对比模型2采用CVaR为目标函数时,获得的收益最大为0.0693。 风险方面,由表12第13列可知,是本模型采用幂风险谱为目标函数时,其风险最小为0.0101。 单位风险的收益,由表12最后一列可知,是本模型采用幂风险谱为目标函数时,其贷款配置结果的单位风险的收益最大为6.73。故本模型为最优模型。 (1)本文通过蒙特卡洛模拟信用等级迁移引起贷款收益的变化情景,并以幂风险谱PSR最小为目标函数,以贷款组合的收益大于目标收益为约束,构建贷款优化配置模型。通过幂风险谱PSR、条件风险价值CVaR、风险价值VaR三种模型对比,实证结果表明基于幂风险谱PSR的贷款配置模型在单位幂风险谱下的收益优于条件风险价值CVaR与风险价值VaR的贷款配置模型。 (2)利用幂风险谱来度量资产组合的风险,通过损失-Xi越大、其风险权重?i也就越大的思路,构建幂风险谱PSR最小建立非线性规划的目标函数,使资产配置的最优组合反映的风险厌恶的价值偏好。即弥补了现有研究条件风险价值CVaR[6-9]仅均等看待尾部风险、忽略风险较大的损失应予以更大权重,也同时弥补了现有研究风险价值VaR[2-5]仅提供某一置信水平下资产损失的最大值、无法反映一旦超过这一数值的可能损失的弊端。 (3)通过蒙特卡洛模拟信用等级迁移引起贷款收益的变化情景,并以信用等级迁移后贷款组合损失越大、则风险厌恶权重越大的思路构建幂风险谱PSR最小为目标函数,以贷款组合的收益大于目标收益为约束,构建贷款优化配置模型,改变了现有研究[2-9]贷款配置时没有同时控制信用风险和尾部风险的不足。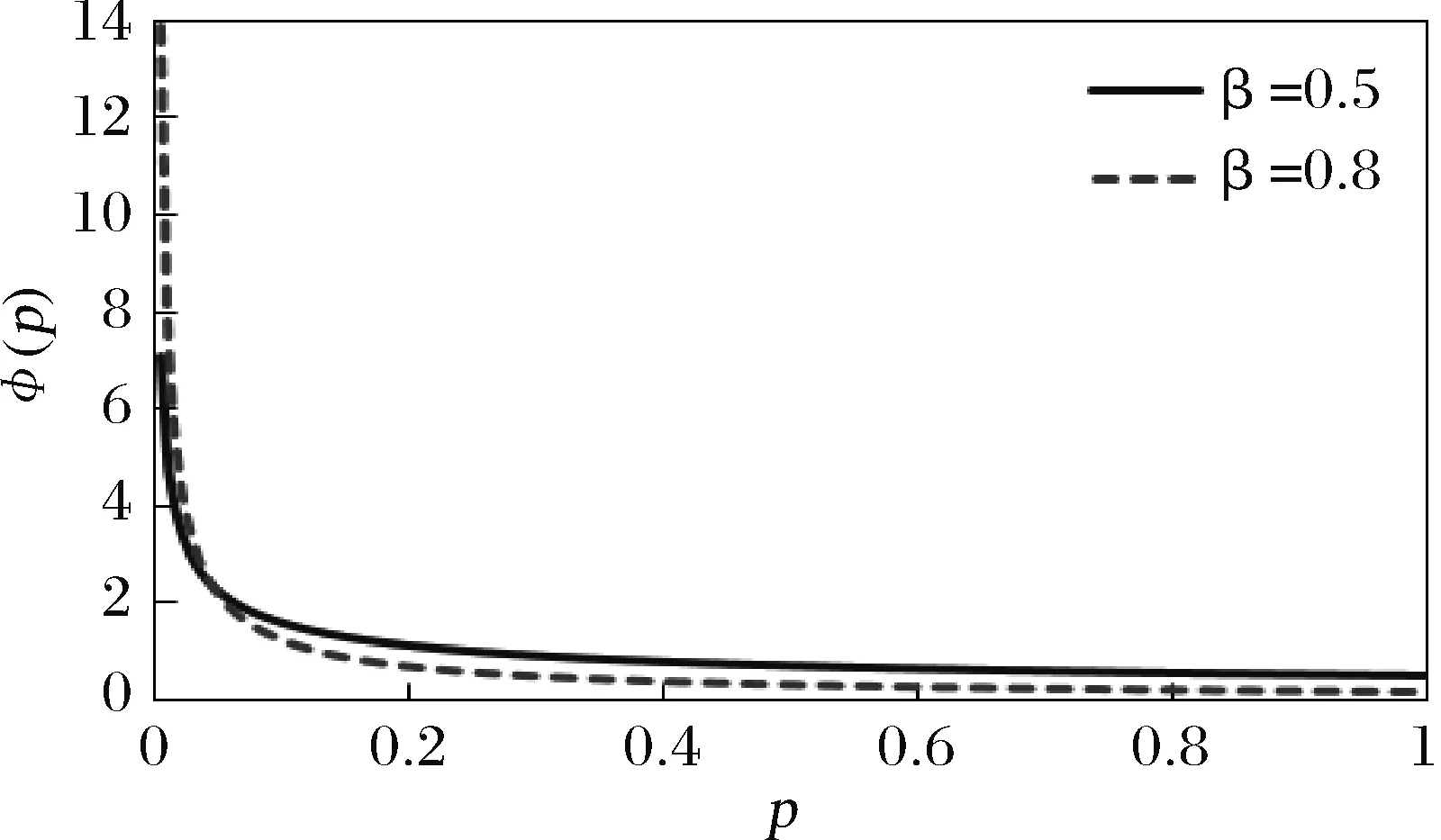

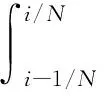
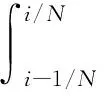
3.2 风险价值VaR和条件风险价值CVaR是本文谱风险的一个特例
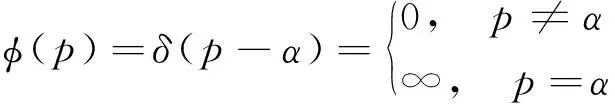
3.3 贷款收益的Monte Carlo模拟

3.4 基于幂风险谱的贷款组合配置模型的构建
4 应用实例
4.1 基础数据
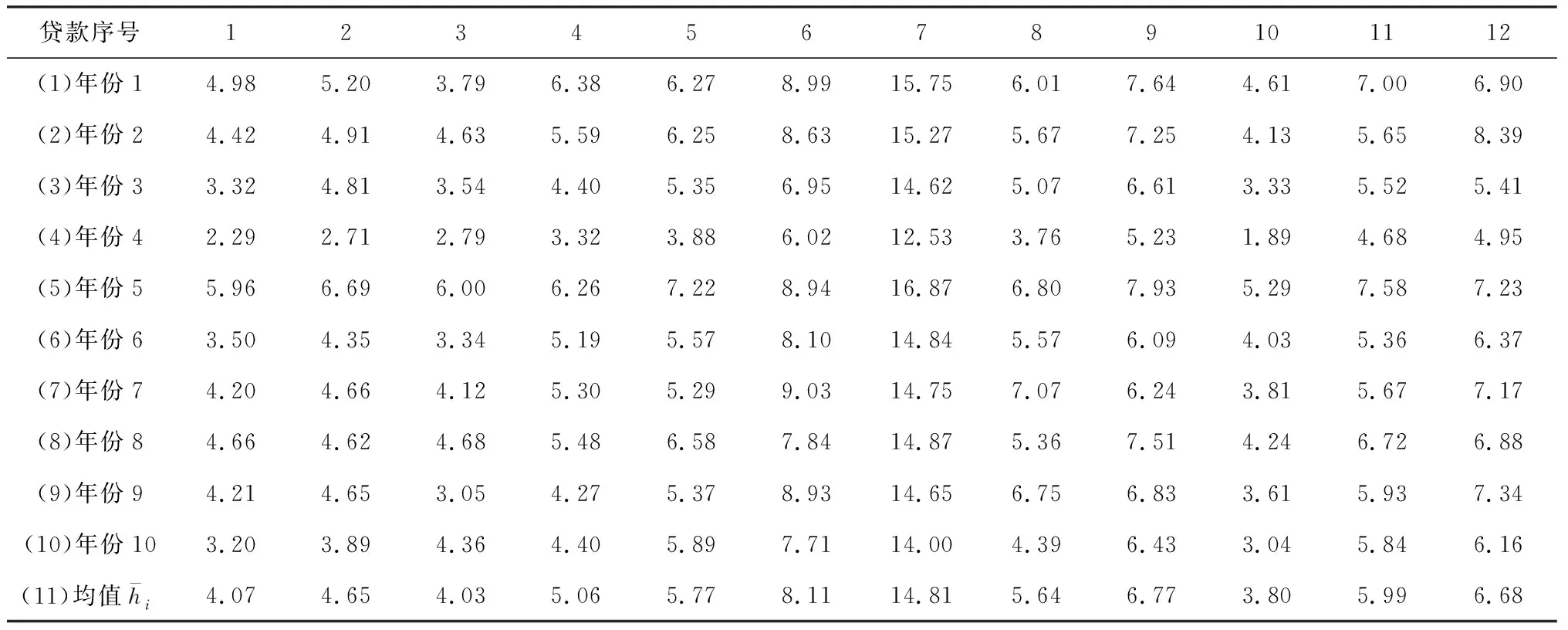
4.2 Monte Carlo模拟贷款收益率
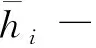
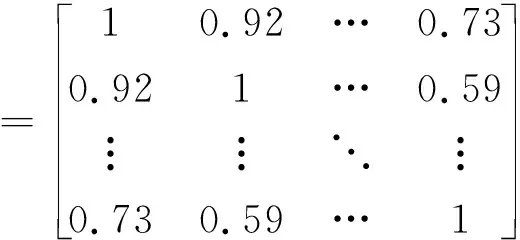
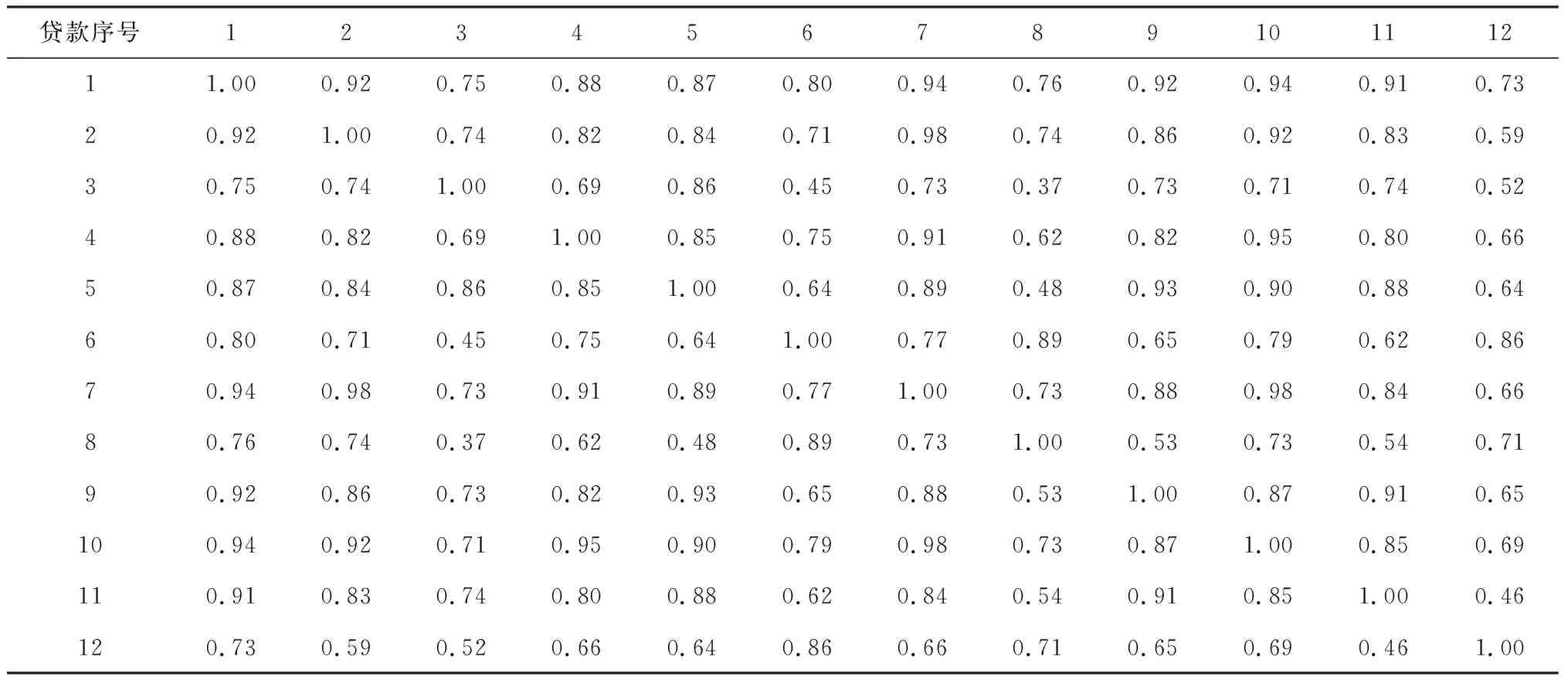



4.3 基于幂风险谱的贷款组合优化配置模型
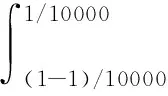
5 模型的对比分析
5.1 对比模型1


5.2 对比模型2
5.3 对比结果与分析
6 结语
