基于连续Hopfield神经网络的立体库路径优化

陈 晨，茅 健 CHEN Chen,MAO Jian

（上海工程技术大学 机械与汽车工程学院，上海 201620）

0 引言

近年来，工业4.0战略规划促使整个工业生产体系进入全新的水平[1]。作为工业4.0的核心组成部分，智能物流是连接客户、供应链和制造业的重要环节，是未来智能工厂的重中之重，堆垛机是智能物流中重要设备之一。其路径的好坏决定了仓库的运作效率，因此对堆垛机的路径规划也成为了研究热点，国内外学者已经做出了很多贡献[2]。

吴高航[3]将基于Hopfield神经网络的方法对TSP问题进行实验，并分析不同能量参数对结果的影响，从而优化参数的选择。陈萍[4]等通过研究Hopfield神经网络求解TSP问题的实例，缩小了网络参数的范围。费春国[5]等利用网络能量变化的性质，稳定了网络能量函数，从而解决了函数易陷入局部最优值和得到无效解的问题。Hajar Asgari[6]等提出一种高效实现Hopfield神经网络的收缩结构，从而提升了系统的运行效率。Zbigniew Nagórny[7]等通过参数自整定，寻求最优路径。Farah Sarwar[8]等详细分析了Hopfield神经网络中参数在不同范围对结果的影响，从而优化算法的收敛速度和精度。

本文根据立体库的实际情况，基于连续型Hopfield神经网络方法，研究了堆垛机运行情况，建立了堆垛机路径优化模型并进行仿真，结果表明该方法能快速，准确地解决堆垛机路径优化问题。

1 问题描述

堆垛机的路径优化首先要对堆垛机的运行情况进行详细的分析。设堆垛机的原点为库格最底层，第一货格左下角处。堆垛机的横向速度为Vx，提升速度为Vy。堆垛机的作业点为货格中心处。在实际生产中，一般都是批次取货。设有n个拣选任务，即有n个货位点等待堆垛机到达，堆垛机从出/入库站台处出发，分别到达n个货位点，且每个货位点只去一次，最后回到起点，求堆垛机运行的最短路径。其简化执行路线如图1所示：

当堆垛机执行1,2,3,…,n条指令时，时间分析如下：

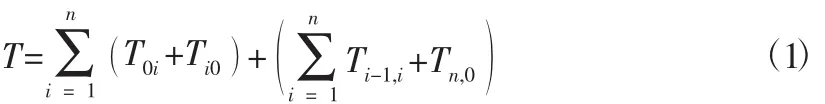
其中：T为执行n条指令堆垛机运行的时间，T0i为从起始点P0到Pi（任务终点）所用的时间，Ti0为堆垛机从点Pi（任务终点）到起始点P0所用的时间，Ti-1,i为从点Pi-1（现在所处货位） 到Pi（下一指令货位）所用时间，Tn,0为堆垛机完成此批次任务后回到原点P0所用的时间。

进一步的分析表明，当一批指令分配给堆垛机时，不管按何种顺序执行指令，第一部分所需要的时间总是相同的，与指令执

行的顺序无关。第二部分为一个从原点出发途径各库位的回路，指令的执行顺序不同将会导致不同的工作时间，工作路径。第一、第二部分示意图如图2、图3所示：

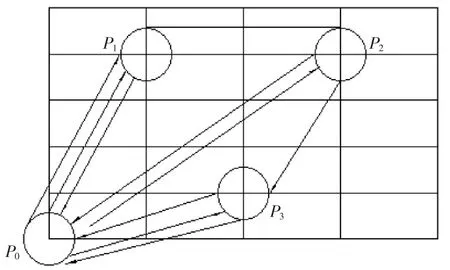
图1 简化复合方式作业示意图

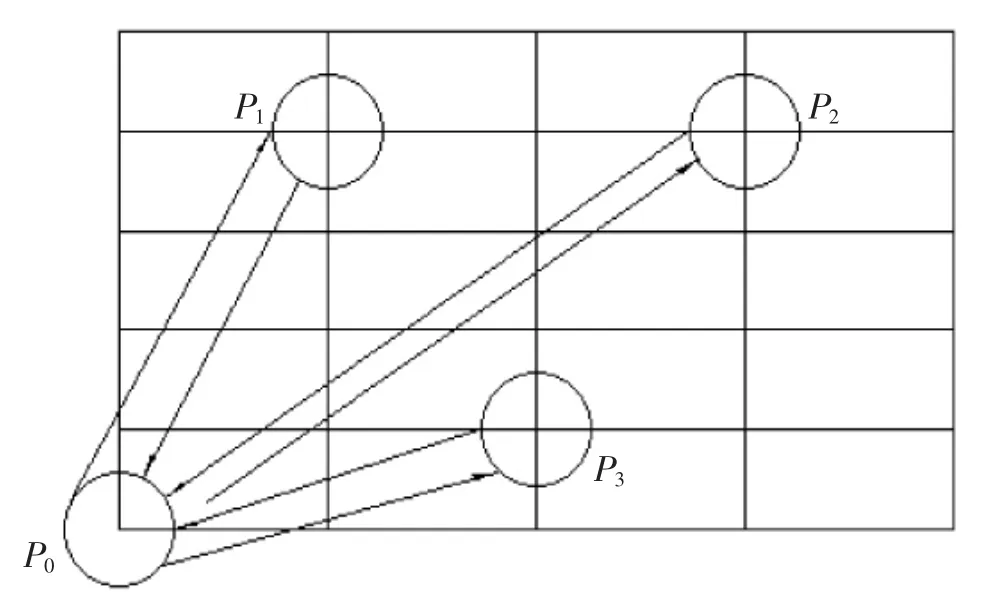
图2 第一部分示意图

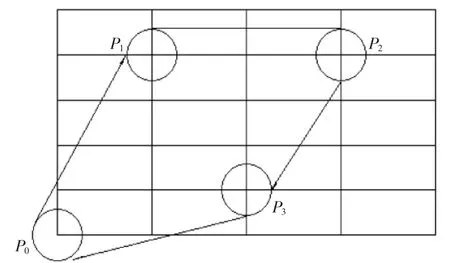
图3 第二部分示意图

2 连续Hopfield神经网络

Hopfield（霍普菲尔德）神经网络是一类单层互相连接的反馈型神经网络，其中每一个神经元和其他神经元相连接。美国科学家J.J.Hopfield（霍普菲尔德）于20世纪80年代将动力学相关思想引入神经网络的构造中，率先提出了此类算法。

在二值神经网络（离散Hopfield神经网络）的基础上，J.J.Hopfield利用模拟电路（电阻、电容和运算放大器）实现了对网络的神经元的描述。假设神经元j（j=1,2,…,n）的内部膜电位状态Uj表示，细胞膜输入电容为Cj，细胞膜的传递电阻为Rj，输出电压为Vj，外部输入电流用Ij表示。其中，Rj和Cj的并联模拟了生物神经元的时间常数，wij模拟了神经元间的突出特性，运算放大器模拟了神经元的非线性特性，Ij相当于阈值。由基尔霍夫电流定律（Kirchhoff's Current Law，KCL）可以得出：

式中：n为神经网络神经元的个数；Vj（t）为输出电位；Uj（t）为输出电位；gj为神经元的传递函数；W=wij（i,j=1,2,…,n）为网络权系数矩阵。

而要使得连续型Hopfield神经网络的稳定性得到保证，需要满足两个条件：第一点，Hopfield神经网络的神经元传递函数g是连续有界的；第二点，网络的权值系数矩阵对称；则可保证这个连续Hopfield神经网络是稳定的。

在实际应用中，如果将一个最优化问题的目标函数转换成连续Hopfield神经网络的能量函数，而问题的变量则用网络中神经元的状态来表示。由此，在组合优化领域，Hopfield神经网络有着广阔的应用。

在本文研究案例中通过上述分析，可知当一批任务确定后，第一部分的值是确定的。第二部分则是一个TSP问题。应用Hopfield神经网络来解决此类问题，将目标函数（最短路径）转换为网络的能量函数，把问题的变量（堆垛机执行任务的顺序）对应到网络的神经元状态。在神经网络和动态系统中，给出初始的统计点，即初始条件，然后随着网络在运动传递中找到相应的极小点，即问题的最优解。

3 优化模型

依据设计思路，将TSP问题映射为一个连续型Hopfield神经网络主要分为以下几个步骤。

（1） 模型映射

为了能让Hopfield算法模型能与实际情况相对应，使用换位矩阵来说明其动态模型。例如，有5个库位甲，乙，丙，丁，戊，到达的顺序是甲→戊→丁→乙→丙，则Hopfield网络输出所代表的有效解对于的二维矩阵如表1所示：

对于N个库位TSP问题，需用N*N个神经元来实现，而每行每列都只能有一个1，其余为0，矩阵中1的和为N，该矩阵称为换位矩阵。

（2）构造网络能量函数和动态方程

上述分析表明，目标函数映射于人工处理后的霍氏神经网络的能量函数E。所以，网络的能量函数E由目标项（最短路径）和约束项（换位矩阵）两部分共同组成。网络的能量函数定义为：

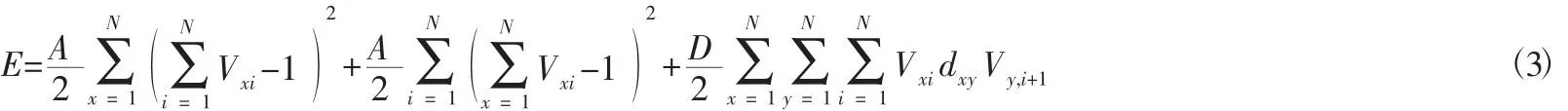
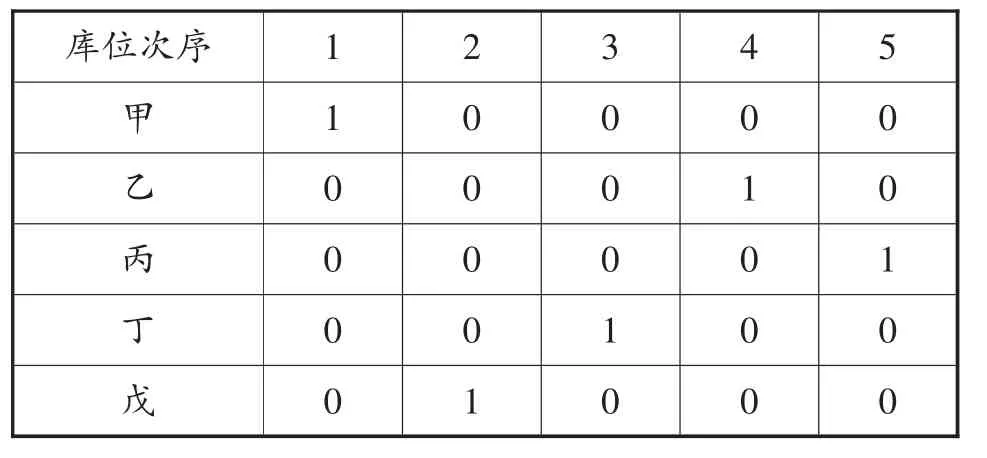
表1 5个库位的访问路线

在这个多项式中，第一项、第二项是问题的约束项，第三项是目标项。相应的Hopfield神经网络的动态方程为：

（3） 初始化网络

Hopfield神经网络的能量函数和动态方程的系数稍有变化，就会对迭代过程有极大的影响。在总结前人经验及多次试验基础上，网络输入初始化选取如下：

式中：U0=0.1；N为库位个数为10；δxi为（-1,+ 1 ）区间的随机值。在式（3）、式（4） 中，取A=200，D=100；采样时间设置为step=0.0001，迭代次数为10 000。

（4） 优化计算

当网络的结构及其参数设计完成后，迭代优化计算的过程就变得非常简单。具体步骤如下：

步骤1：导入N个库位的位置坐标并计算库位之间的距离；

步骤2：网络初始化；

步骤5：利用式（3） 计算能量函数E；

步骤6：判断迭代次数是否结束，若迭代次数k＞10 000，则终止，否则k=k+1返回步骤3。

4 实例分析

为了验证方法是否可行，选取某公司精密零件仓库为例。货格规格为100mm*100mm，每个货架分为10层，10列。堆垛机的横向速度和纵向速度相等，而且由于零件的特殊性，堆垛机的作业点在货格的左下角。货格编号如表2：

表2 货格编号

某批出入库任务如表3：

表3 任务表

利用MATLAB软件对案例进行仿真，并分析得到的结果。

图4为随机产生的初始路径，所经过的路径为3→5→4→6→2→7→9→8→1→10，其长度为5.1852m。

图4 随机产生的初始路径

经过连续型Hopfield神经网络优化后，由图5可知，寻找到的优化路径为3→5→4→6→10→9→8→7→1→2，其长度为3.1876m。

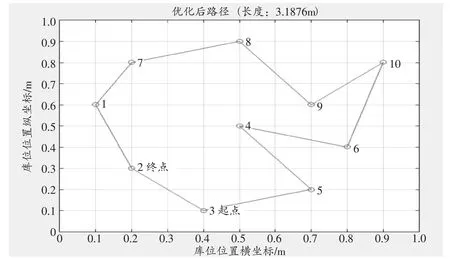
图5 Hopfield网络优化后路径

能量函数随迭代过程变化的曲线如图6所示，从图6中可以清晰地看出，随着迭代的进行，网络的能量明显地呈下降趋势。当能量起伏曲线趋于稳定时，意味着神经网络趋于稳态。也就是说，堆垛机路径优化的最优解已经求出。

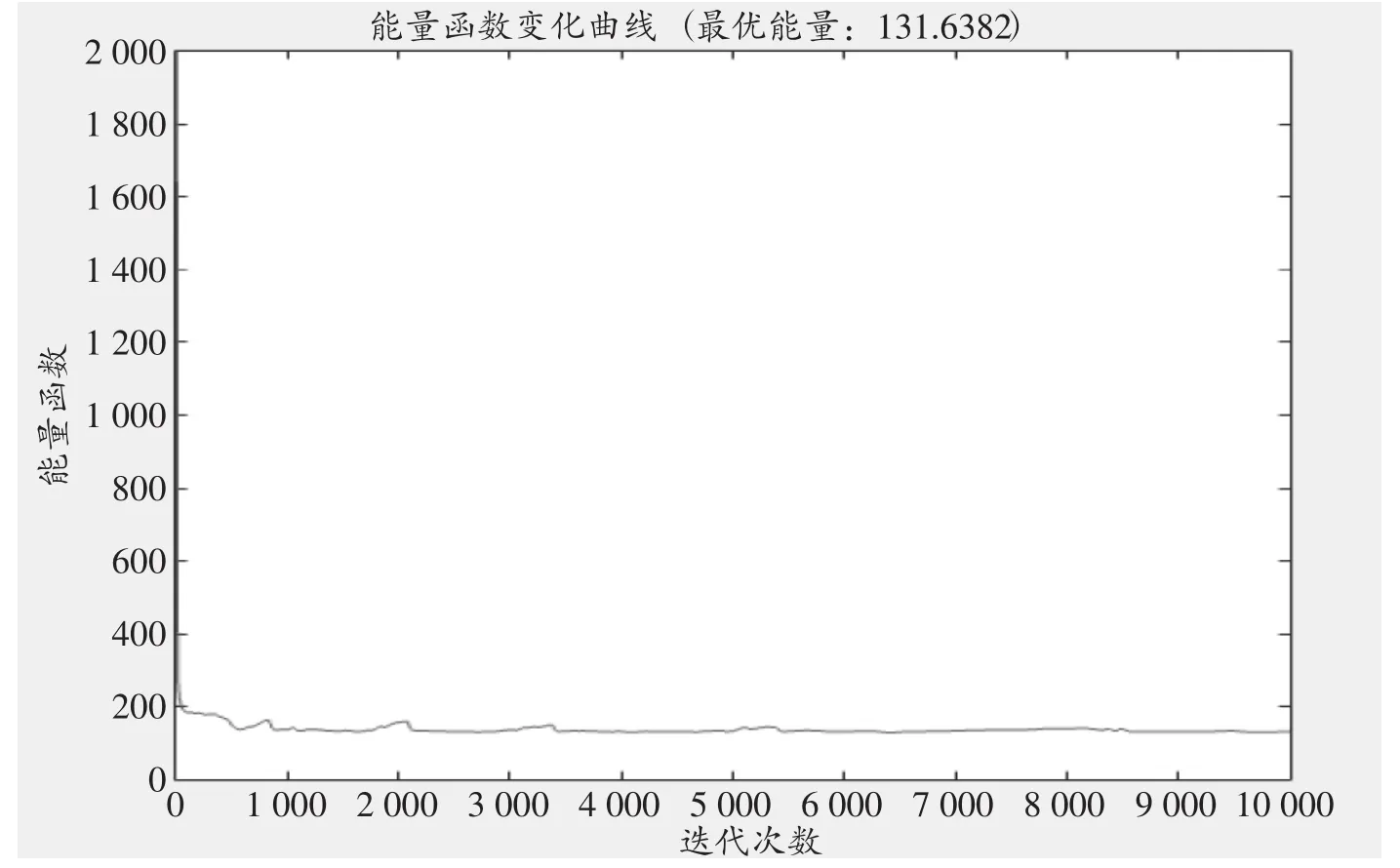
图6 能量函数随迭代次数变化曲线

5 结束语

在分析堆垛机运行情况并建立相应模型后，通过仿真实验及数据对比，验证了本文提出的连续型Hopfield神经网络算法在解决立体库堆垛机路径优化问题的有效性。利用连续型Hopfield神经网络，可以快速准确地解决此类问题。实验数据也为自动化立体库的设计规划提供了的理论参考依据。