基于双约束重力模型的5路环形交叉口车流量预测研究
——以上海五角场为例
2019-02-14徐翔宇马晓旦上海理工大学管理学院上海200093
徐翔宇,马晓旦 (上海理工大学 管理学院,上海 200093)
0 引言
调查统计数据显示大多数的5路环形交叉口一般位于城市交通咽喉。因此,如果对该类型的交叉口研究得不透彻,处理不妥当,将非常影响城市交通的畅通性[1]。该类型的交叉口需要研究的层面很多,本文主要研究5路环形交叉口交通流流向计算的问题。
环形交叉口按照进口道的数量,最常见的可分为3路、4路和5路环形交叉口,如果是3路或4路环形交叉口,通过实际调查,可以得到进口交通量、出口交通量、进口右转交通量和交织横断面交通量4项基本数据,并通过计算得出各进口流量对交通量的影响。但是,这种方法不适用于5路环形交叉口,由于5路环形交叉口方向数目的增加和交通组织的更加复杂,路口方向分布的计算越来越困难[2-4]。
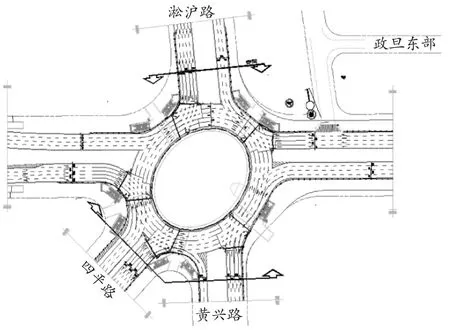
图1 交叉口几何结构图
上海市五角场有翔殷路、淞沪路、邯郸路、四平路、黄兴路5个路口。由于各路口流至其他方向的车流量难以调查,加上中间有环岛,视线有所被阻挡,调查的难度更大,因此,确定五角场的交通流向难度极大,由前期调查,使用CAD绘出上海五角场的几何机构示意图如图1所示。
五角场每个入口的交通流有4个方向,总共有20个方向。只有每个入口右转的交通流才能通过直接观测来测量。余下的15条交通流仍有待解决。因此,如果直接通过观察,无法计算出每个方向的交通流量。这就需要本文后面提出的方法和模型进行求解。
1 方法介绍
本次调查的方法为人工计数法,这也是交通调查最常用的方法。本次调查安排了5个记录员,于2018年9月2日下午15:00时,在五角场的5个进口道记录右转交通量和所有进出口交通量,并记录标记车辆(包括交通量和车型),测得的结果如表1与2所示:

表1 各路口实测右转车辆数
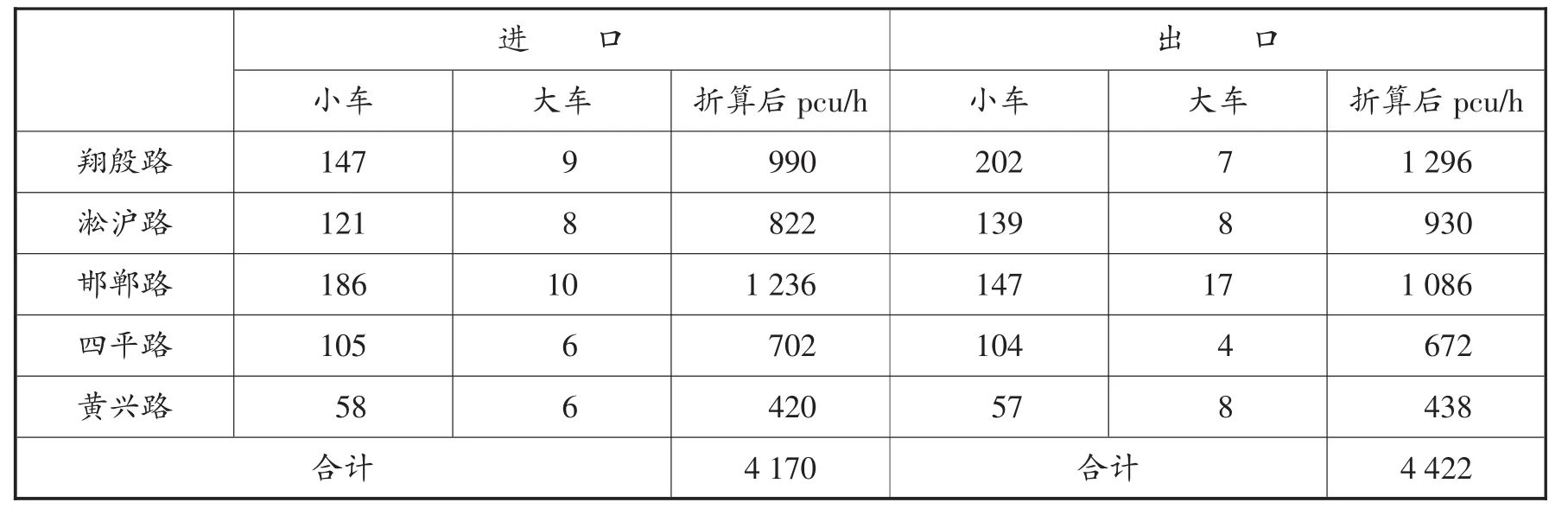
表2 交通初始量
2 构建模型
2.1 模型建立
对于5路环形交叉口,各方向的交通流流向无法直接通过观测得出,但利用交通分布预测的重力模型法可以分析流量流向。假设交叉口的进口和出口分别为出行起点和出行终点,则进口流量和出口流量分别相当于出行生成量和出行吸引量,则通过交叉口进出口流量来计算各流向流量的问题,就可转化为已知交通发生量和吸引量求交通分布的问题,即交通分布预测。在环形交叉口中,假设从第i路口进,从第j路口出,交叉口的流量Tij与调查时段内第i路口进入交叉口的交通量Ii和第j路口离开交叉口的交通量Oj的乘积成正比(与距离无关),因为各路口之间的交通流向与它们之间的距离无关。由于交叉口的回头车所占比例通常较小,可以近似认为0,如果遇到更多的车辆,通过调查和确定的比例,在流量分析时直接删除,从而构建一个虚拟交通阻抗矩阵R对角线元素到正无穷,其他元素全部为1[5-10]。
ij
为了保证ΣiTij=Ij及ΣjTij=Oi,必须同时引进行约束系数Ki和列约束系数,构造双约束重力模型如下:

在环形交叉口流量的实际调查中会存在一些误差,驶入交叉口的交通流量之和与驶出交叉口的交通流量之和不可能完全吻合。为了确保调查时段内通过环形交叉口的交通流量之和T=ΣiΣjTij=ΣiIj=ΣjOi,必须预先处理一下调查数据,以较大的数据作为标准值,并将两者的差值与较小的数据进行等分,以确保交叉口入口流量等于出口流量。否则,在进行Ki与迭代的过程中不会收敛。
2.2 算法步骤
(1) 首先命令各个列约束系数为=1(j=1,2,…,n);
(2) 其次将各列约束系数K'j=1(j=1, 2,…,n)全部代入式(2) 求得各个行约束系数Ki;
(3) 得到了的行约束系数K(i=1, 2,…,n)全部代入到式(3) 中求各个列约束系数;
(4)比较前后两批的约束系数,并检验相对误差是否小于3%。如果是这样,则将相对错误更改为步骤5,否则改为步骤2;
(5) 用最后约束系数Ki,代入式(1) 中求出各交叉口的流向,终结算法。
2.3 交通量计算
从表1可以看到驶入的和驶出的流量之间差异是252,误差是5.8%,是在允许的错误范围内。把252按比例分摊到进口流量上面去,使进出流量平衡,得到进口流量分别为1 049.8,817.7,1 310.7,744.4,445.4。
根据算法要求,应用Matlab程序编辑代码,得到结果如图2所示:

图2 交叉口几何结构图
2.4 算法输出
根据Matlab语言输出Ki,两数的值,具体见表3。

表3 算法输出结果
根据Matlab语言输出翔殷路、淞沪路、邯郸路、四平路、黄兴路5个进口道到各自的4个出口道的相关流量。由于淞沪路与黄兴路双向间存在下穿通道,故淞沪路与黄兴路环岛绕行的车辆数近似为0。具体数值见表4、表5所示。
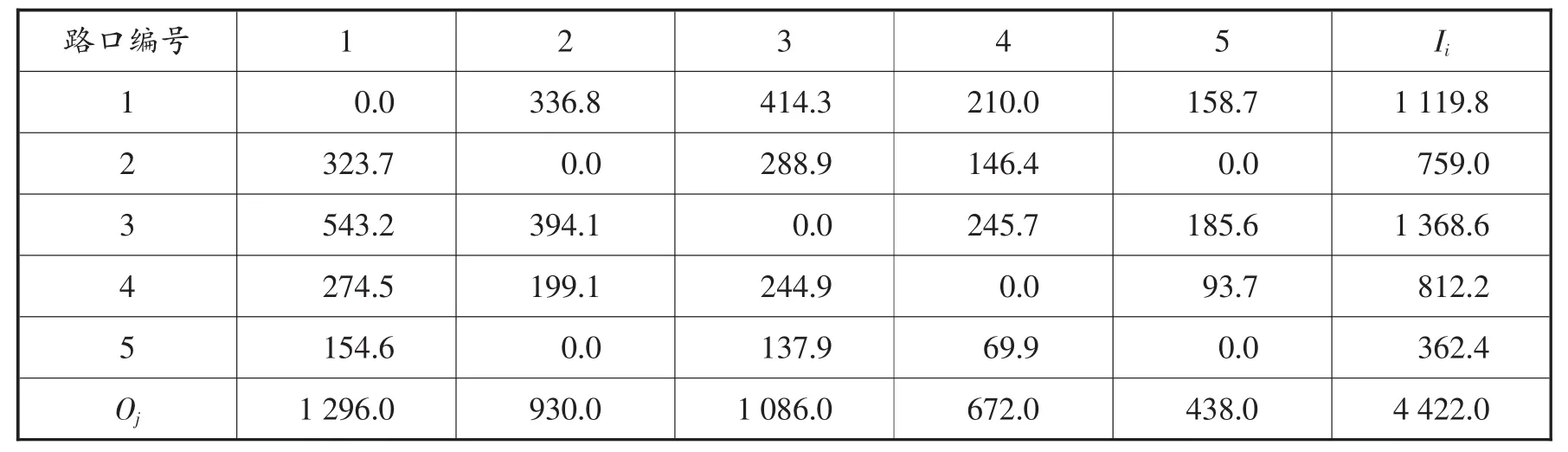
表4 各流向交通量
根据计算所得各路口右转车辆总值为1 192辆,现场调查所得各路口右转车辆总值为1 078辆。此双约束重力模型法计算所得误差为9.5%左右。
3 结论与展望
由双约束重力模型可以看出,只要调查其中一个进出口断面通过的车流量,就可以计算出交叉口所有方向的车流量。因此,双约束重力法只需测量少量的数据,可以大大降低调查强度。同时调查数据要求的精度不高。采用迭代算法计算了较为合理的流量结果,该方法适用于5路环形交叉口或更多路线的环形交叉口。
但是由于城市道路交叉口的形式各有不同,信号控制也有所区别,各个5路环形交叉口道路资源也不尽
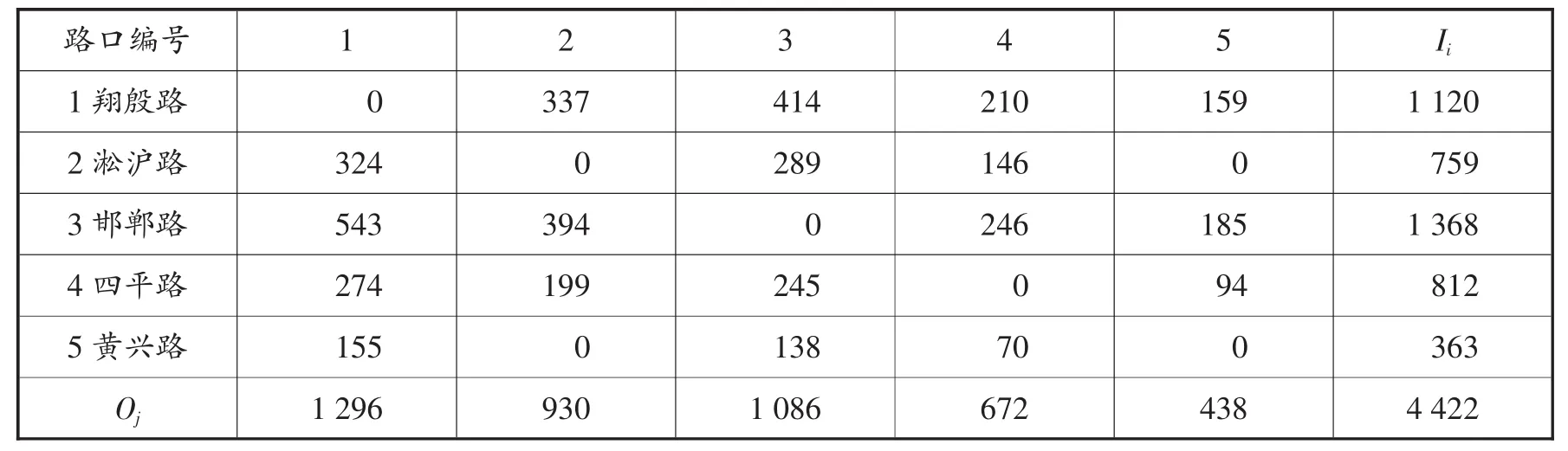
表5 输出数据量化
相同,加上交通流的大小按时间不同也要分高低峰,因此上述模型不能包含所有的情况和条件,仍有待深入研究。
