关于动脉粥样硬化斑块有缺陷时的力学应力分析
2019-02-13王练妹胡继文雷卫瑞刘文一刘亚涛
王练妹, 胡继文, 雷卫瑞, 刘文一, 刘亚涛
(南华大学 数理学院,湖南 衡阳 421001)
动脉粥样硬化是引起心血管疾病的主要因素,其临床表现包括缺血性心脏病、中风和外周动脉疾病等[1]。动脉粥样硬化(Atherosclerosis,简称AS)斑块会受到各种生物应力作用,这些生物应力可能超出斑块材料承受的破裂阈值。一般认为,易损斑块的特征是脂质核较大、纤维帽较薄,其中生物应力在早期的动脉粥样硬化斑块形成、进化和破裂中起着重要作用[2,3]。周向峰值应力(Peak Circumferential Stress,简称PCS)被认为是决定生物力学的重要因素,是导致动脉粥样硬化斑块破裂的基本动因,也是研究最多的物理量,通常被看用作是动脉粥样硬化斑块破裂位置的预测因子[4]。
在PCS的研究中,最初使用二维模式来描述和分析。近年来,将三维有限元分析(Finite Element Analysis)和流固耦合模型相结合,试图将PCS与组织材料特性和斑块几何形状(更具体地说是纤维帽厚度和坏死的核心大小)联合起来综合分析[5~7]。二维模式研究表明:PCS发生在高坏死核心区、且曲率较大的纤维帽肩部处。但实验表明,多达40%的破裂发生在纤维帽的中心及其它的位置处,其中PCS阈值明显变小[5]。为解释相关实验现象,研究人员提出了一种关于纤维帽破裂的“替代假说”,即纤维帽内存在与巨噬细胞差不多同样大小的微钙化区,钙化区的存在导致了斑块的不稳定性。这一假设可以得到斑块钙化时的PCS是均匀厚度区内纤维帽应力的两倍,将使得纤维帽从界面剥离而发生破裂,解释了在纤维帽的中心可能发生破裂原因。即使纤维帽厚度大于65微米,纤维帽内依然出现大于300kPa的PCS[7]。Vengrenyuk等人做了进一步的研究,结果表明,如果纤维帽内的微钙化区被拉长,则厚度标准可以显著增加,即厚度大于100微米的纤维帽也有破裂的风险[8],该实验支持了“替代假说”。
除“替代假说”外,在对AS进行影像技术处理后的结果报告中发现,破裂并不总是因纤维帽钙化而产生,而在纤维帽附近的小空穴处同样会引起斑块破裂[9]。同时尸解结果表明,小空穴通常是由小于10微米、早期坏死的肌细胞间隙造成,且通常存在于脂质核和AS纤维帽间的过渡层区域内[10,11],我们称这种结构为组织局部缺陷。过渡层中或过渡层边缘含缺陷的复杂结构可能是斑块破裂的重要原因,目前少有相关物理模型对其进行描述,这也是本文研究目的所在。
根据上述相关研究报告,本文提出了一个不稳定性AS斑块模型假设,即AS斑块中存在一个过渡层,过渡层中或过渡层边缘包含一些微小缺陷(空穴或钙化区)。本模型假设主要受橡胶轮胎中微小固体球形杂质作为轮胎材料功能失效的理论结果影响[12]及Gent和Park等人的后续实验结果[13]:杂质会引起材料硬度等功能的不匹配性,这种不匹配导致材料沿着拉伸轴方向在杂质极点处产生的局部应力集中,从而导致固体杂质和橡胶之间的界面处发生剥离;另一方面,AS斑块影像及尸解结果表明,在斑块纤维帽下方存在一个包含空穴或钙化区的过渡层。本研究首次创建了一个包含过渡层的AS斑块理论模型,并运用有限元法对AS斑块进行二维应力分析,探讨AS斑块不稳定性的物理机制。
1 模型和方法
1.1 边界条件
假设血管壁为刚性壁面,不随管内流体运动而变形[14]。流体的粘性条件如下:
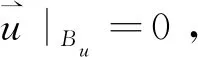
(1)

u_mean*6*(H-Y)*Y/H2,
(2)
其中u_mean表示平均速度,且满足下述等式:
u_mean=U*t2/sqrt(t4-0.007[s2]*t2+0.0016[s4]),
(3)
其中,U=33.7cm/s为入口处的稳态平均速度,H是血管直径,Y是内部结构的径向位置。流固边界处流体速度和纤维帽运动速度相等,并保持机械力平衡[15],即保持固体内部边界的位移连续性和机械平衡:
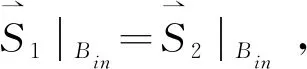
(4)
其中,Bin是固体内部边界。斑块的底部固定在血管壁上,且满足如下等式:

(5)
1.2 几何模型
假设过渡层内缺陷区位置分别为x=(10~12,12~14,16~18)mm三个区域,其余位置材料均质等厚。具体按如下模式设置:a)三个区域具有与纤维帽相同的材料特性(纤维帽);b)三个区域具有与脂质核相同的性质(脂质核);c)三个区域具有与空气相同的材料特性(部分空穴);d)三个部分具有与钙化相同的材料特性(部分钙化)。
均匀过渡层由20个均匀单元组成,非均匀过渡层中的杨氏模量取20个随机生成的值([0.8-1.2]*E4)。模型结构相应的参数值由表1给出[16,17]
根据假设建立如图1所示的模型结构:过渡层的分布类型(非均匀过渡层,部分过渡层缺陷,均匀过渡层)。动脉的长度和直径分别为28mm和10mm[18];斑块模型是半椭圆形,其短轴和长轴分别为7mm,6mm[18]。建立有限元矩阵方程,对整个区域进行网格划分。在流固耦合模型中,使用单位大小的自由三角形网格划分模型:血管壁由5878个网状顶点和11480个三角形单元组成,斑块由2632个顶点和5066个三角形单元构成。此外,血液包含2846个顶点和5408个三角形单元。

表1 结构参数的值
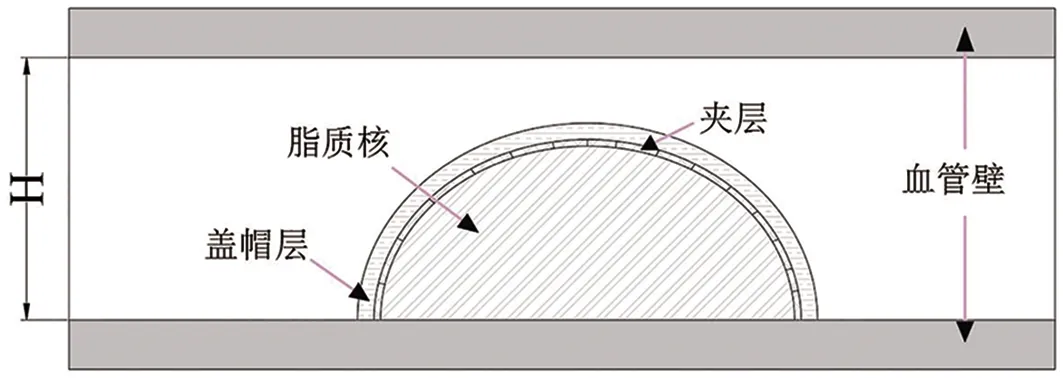
图1 几何结构模型
1.3 流体模型
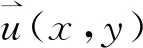
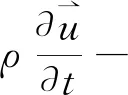
(6)
-
(7)
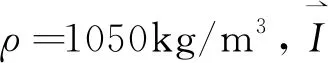
在血管入口处,流体以层流形式流入,流速按抛物线分布,但其幅度随时间变化:
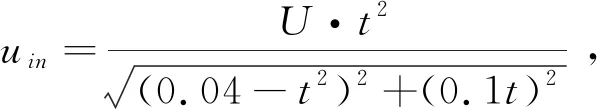
(8)
方程(8)中的t为秒计,在出口处(血管右端),设定相对声压值为0。
1.4 固体模型
斑块由纤维帽、过渡层和脂质核组成。运用线弹性理论及以非线性结构理论求出斑块内应力分布及变形。斑块被固定在下血管壁底部,血管内所有其他边界都受到流体施加的载荷作用,并用方程(9)表示:
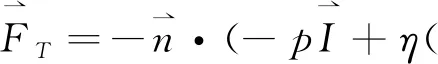
(9)

2 结果与分析
使用流固耦合模型针对不同过渡层结构的斑块应力分布进行分析,通过应力曲线评估斑块的稳定性。图2显示了非均匀过渡层的二维FSI模型的流场和应力场分布。从图中可知最大应力发生在AS斑块左肩部,达到78kPa。而最大流速流速则位于斑块最顶部,达到了3.2m/s.斑块内其它处应力分布较为复杂。
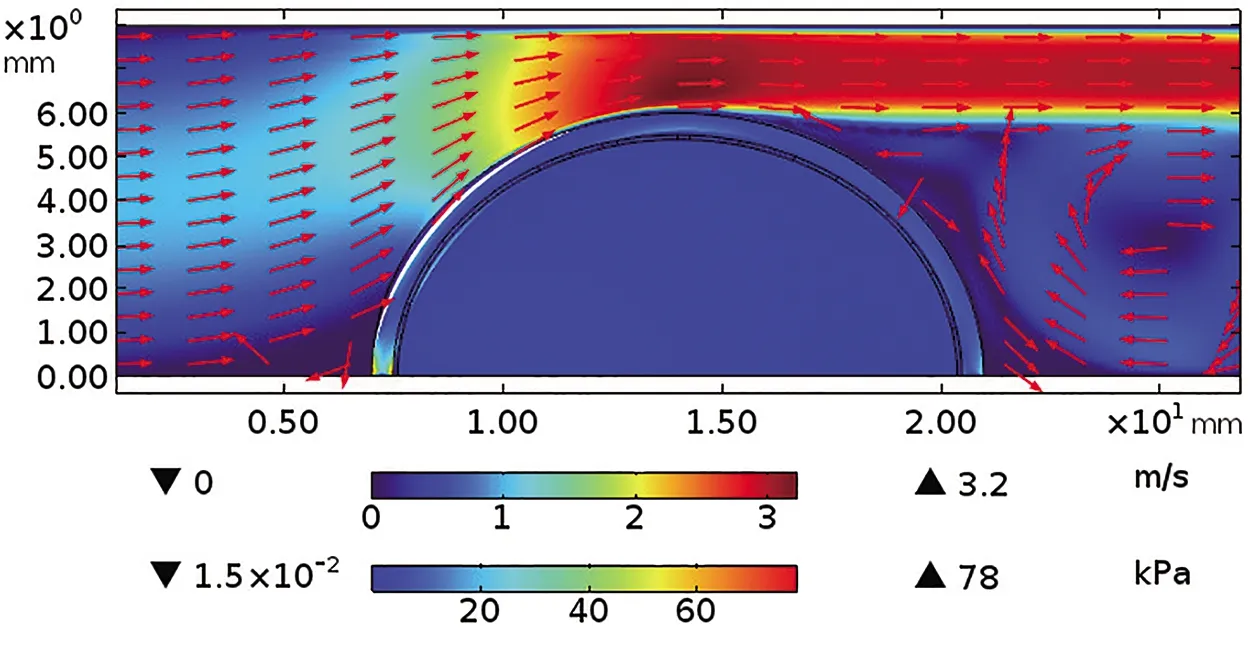
图2 动脉的速度分布和斑块的应力分布,纤维帽厚度为50微米,过渡层厚度为10微米动脉的模拟结果
图3通过应力分布直方图对均匀和不均匀过渡层上的斑块力和过渡层的部分缺陷进行了比较:
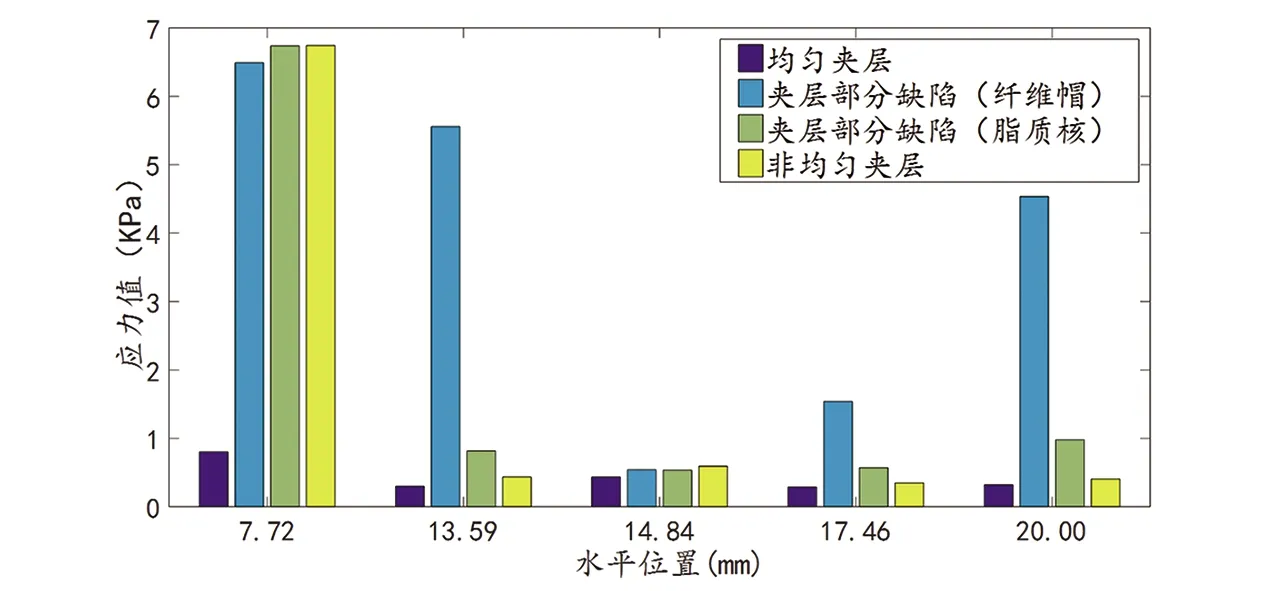
图3 在均匀过渡层,过渡层部分缺陷,非均匀过渡层三种情况下的斑块应力分布
过渡层中有缺陷位置处的应力明显高于均匀和不均匀的过渡层同等位置处的应力。从图3中应力直方图可看出:斑块内的应力分布受到不同类型过渡层的显著影响。对有部分缺陷的过渡层,观察到最高应力为6.85kPa。与其它三种类型过渡层相比,均匀过渡层各处对应位置处的应力都表现为最低。当x=7.72mm时,即斑块的肩部处,对应于四种过渡层分布的斑块的应力都达到最大值。然而,在x=13.59mm,17.46mm,20.00mm处,具有部分缺陷的过渡层(假设a)的纤维帽上应力值最大,分别为5.85kPa和2.85kPa,4.9kPa。同时,假设b中的应力值是同一位置的第二大值。如上所述,该结果表明在x=(12~14,16~18,20~21)mm三位置的过渡层应力随参数有较大变化,这表明过渡层的部分缺陷增加了斑块破裂的风险。
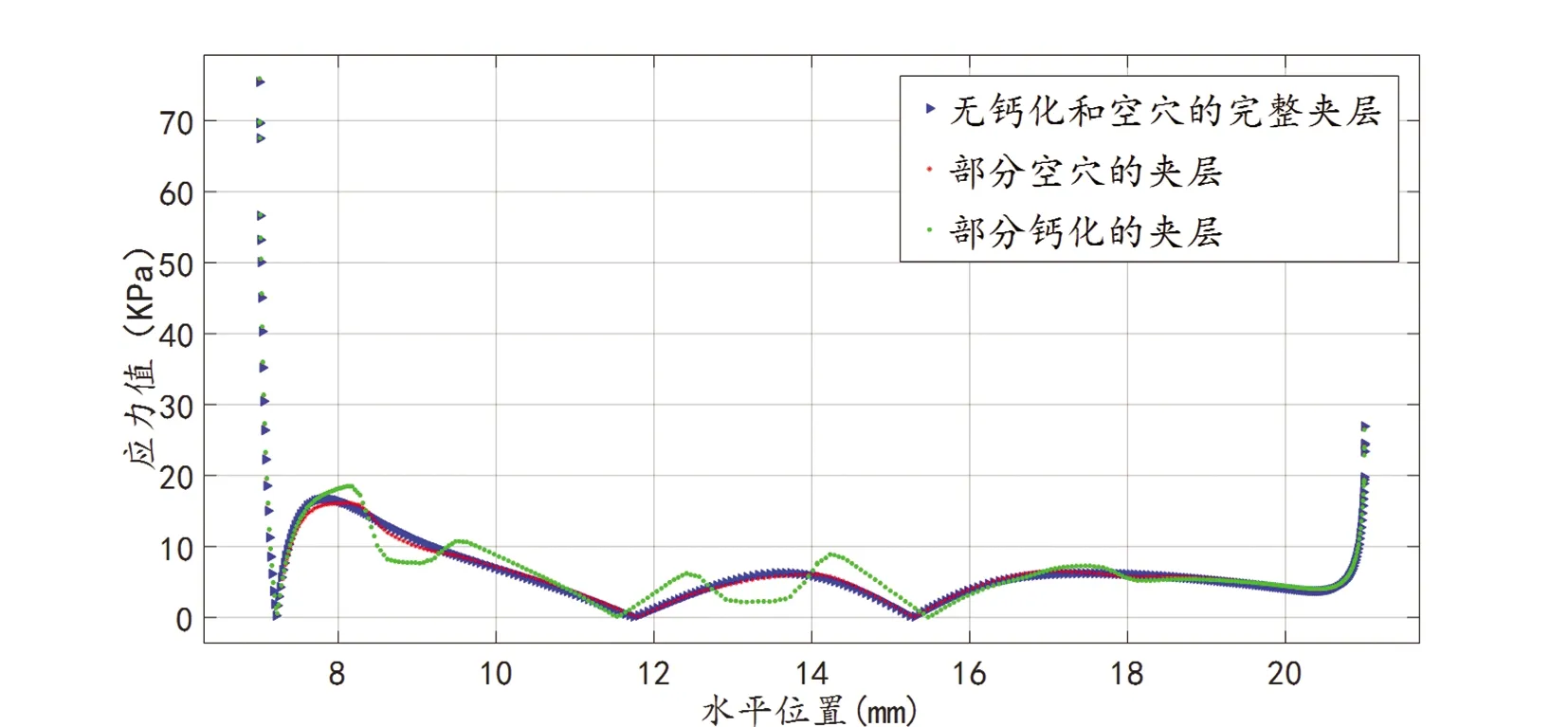
图4 三种情况下纤维帽外表面应力的比较
图4显示了图3中三种缺陷条件下纤维帽的外表面的应力分布。三条应力曲线形态比较接近,变化并不明显,且最大值均分布在斑块的肩部,约为78kPa。对于图4中的应力分布,可能是有缺陷的过渡层出现应力集中,且只对缺陷附近组织的应力改变较大,对远离缺陷区的纤维帽外层影响相对要小。由此可推断,对接近缺陷区的纤维帽内表面和脂质核外表面的应力分布应会有比较明显差别。图5描述了三种条件下过渡层中的峰值应力分布,图中显示了钙化和空穴对应力的影响。图中最左侧,蓝色曲线(无钙化或空穴时)
具有高达44kPa最大应力值,而在x=(8~10,12~14,16~18)mm之间,红色曲线和绿色曲线的峰值应力比蓝色曲线(无钙化或空穴时)变化较为显著,并在缺陷区域的每个位置有两个峰值。相对于有部分空穴过渡层的红色曲线的应力分布,绿色曲线(部分钙化)的应力变化尤为显著。它有一个清晰的驼峰型的分布。最大峰值为34kPa。由此可见,除左端肩部容易产生撕裂外,在钙化区域附近的纤维帽内表面也具有较大的破裂概率,计算结果与文献[5]中的观察结果具有类似的结论。
图5 三种情况下纤维帽内表面应力的比较

图6 三种情况下脂质核表面应力的比较
过渡层钙化或有空穴时对该区域内的应力分布影响还可以从脂质核表面应力分布曲线中观察到。如图6所示,当x=(8~10,12~14,16~18)mm时,红色曲线(部分空穴)中的最大应力是蓝色曲线(均匀过渡层)相同位置应力的三倍,而绿色曲线(部分钙化)的应力值几乎是蓝色曲线(没有空穴或钙化)的6倍。值得庆幸的是,脂质核表面的应力相对较小,斑块在此位置造成撕裂的可能性相对纤维帽的上、下面应力分布要小很多,最大值(红色曲线)为11.8kPa,但同样有造成AS斑块不稳定的潜在风险。从图中还可以看出,脂质核左右两端的应力峰值相对较小。过渡层周围斑块的应力分布与血管内超声造影观察结果具有相似性结论[19]。由此得到,有缺陷的过渡层对盖帽应力分布有显著影响。
3 结 论
本文依据动脉粥样硬化斑块的影像及相关尸解报告结果,建立了一个二维流固耦合计算模型,借助有限元法计算了有空穴或微钙化的过渡层内的斑块应力分布,得到了局部钙化区域易引起应力集中,增加斑块不稳定性、甚至破裂风险。另一方面,过渡层空穴的存在也会出现应力集中效应,导致结构不稳定,但其破裂效果相对于局部钙化要小。综上所述,过渡层中微小缺陷的存在是导致斑块易损性的重要因素之一,也是评价斑块破裂风险的指标之一。应该强调的是,目前的理论模型只是为了证实我们的模型假设,除通常在动脉粥样硬化斑块的肩部处有较大应力外,在纤维帽中有缺陷区域同样产生较大的应力。虽只是建立了一个简化模型,但该模型揭示了血流作用下斑块应力分布的特点,这可能对斑块的不稳定性或易损性评估具有重要理论意义。
