基于裂缝尖端应力强度因子的裂缝穿层行为分析

李浩哲，姜在炳，范 耀,2

(1.中煤科工集团西安研究院 资源勘探开发与瓦斯防治技术研发中心，陕西 西安 710077； 2.煤炭科学研究总院，北京 100013)

引 言

对于水力压裂裂缝在地层界面处的延伸行为，国内外专家学者已经开展了一定的物理模拟研究和数值模拟研究[1-13]。现有的水力压裂裂缝扩展分析中，常用欧文(Irwin)裂缝扩展准则判别裂缝是否延伸[14]，即当裂缝尖端应力强度因子大于地层的断裂韧性时，裂缝发生扩展。因此，研究裂缝穿层扩展过程中应力强度因子的变化对于分析裂缝的穿层行为具有十分重要的意义。而目前的研究主要是对裂缝穿层延伸影响因素的定性分析，对于裂缝穿层过程中裂缝尖端应力强度因子的变化规律则研究较少。本文基于应力强度因子理论，分析了界面处裂缝尖端应力强度因子的变化规律；应用数值模拟，研究裂缝在砂岩-泥岩界面和粉砂岩-煤层界面处的穿层延伸行为，探讨了界面两侧岩石力学性质对裂缝穿层行为的影响，并应用研究成果开展案例分析。

1 界面处裂缝尖端应力强度因子分析

1.1 层状地层模型与基本假设

裂缝在层状地层界面处的扩展模型如图1所示。假设裂缝尖端距离地层界面距离为a，界面两侧岩石力学性质不同，以μi,νi(i=1,2)表示界面两侧材料的剪切模量和泊松比。为适当简化计算，假设界面两侧为弹性均质材料，岩石的断裂行为满足线弹性断裂力学，并且岩石断裂形式为Ⅰ型断裂。目前对于层间界面的研究包括两类[13-14]，即非胶结界面(界面的上下两层只是接触关系，中间不存在胶结物)和胶结界面(上下两层界面之间存在着胶结物，将上下两岩层胶结在一起)。本文研究界面为非胶结界面。

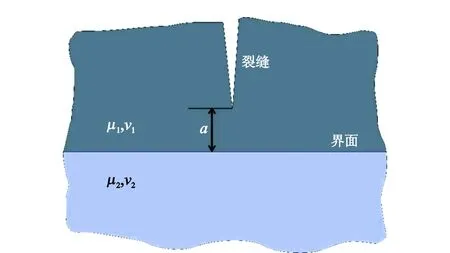
图1 层状地层界面处裂缝延伸示意图Fig.1 Schematic diagram of fracture extension at interface of layered strata

1.2 裂缝尖端应力强度因子

根据以上假设，距界面为a的裂缝尖端Ⅰ型应力强度因子KI为[15]

KI=c(α,β)kIaλ-1/2。

其中：kI为载荷系数，与裂缝内部压力成正比；c为无因次量，是Dundurs参数α,β的函数[16]，α,β取决于界面两侧材料性质，即

λ为Zak & Williams方程的实根[17]，其大小与Dundurs参数α,β有关，即

从式(1)可以看出，若λ<1/2，当a→0时KI(a)→，即裂缝尖端应力强度因子迅速增大，根据欧文(Irwin)裂缝扩展准则，裂缝可直接穿层延伸；反之，若λ>1/2，则当a→0时KI(a)→0，裂缝尖端应力强度因子将随着裂缝与界面距离的减小而减小，裂缝穿层趋势受到限制，可能表现出复杂的扩展特性，如停止扩展、沿界面扩展、拐折扩展等。由此可见，λ对于裂缝在界面处的扩展行为影响较大。

从式(4)可知，λ的大小受到α,β的共同影响。采用数值解的方法，绘制λ-(α,β)关系曲线如图2所示，其中，α∈(-0.95,0.95),β∈(-0.45,0.45),λ∈(0,1)，为岩石力学性质的常见范围[18]。从图中可以看出，当α,β均较大时，λ较小。

图2 λ-(α,β)关系曲线Fig.2 Relation curve between λ and α,β

如上文所述，λ与0.5的相对大小决定了裂缝尖端I型应力强度因子的变化趋势。令λ=1/2，化简式(4)可得

α=-β。

α,β关系曲线如图3所示。对于不同的岩石力学性质，可通过计算得到不同的α、β，图中直线右侧区域满足λ<1/2，直线左侧区域满足λ>1/2。

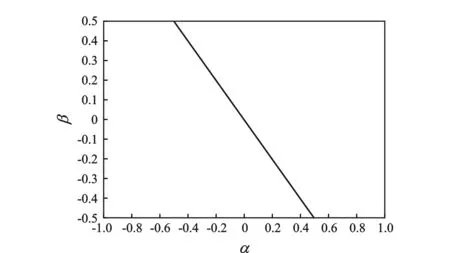
图3 α,β关系曲线Fig.3 Relation curve between α and β

将式(2)、式(3)代入式(5)后化简可得界面两侧材料的剪切模量和泊松比的关系为

引入比例χ=μ1(3-4ν2)/μ2(3-4ν1)，可得当χ>1时，α>-β，此时Zak & Williams方程的实根λ<1/2，裂缝可顺利穿层扩展；反之，当χ<1时，裂缝穿层扩展将受到影响。B.Nuller等[18]将该系数称为界面强度系数(ITI)，通过该系数可以判断裂缝在界面处的扩展行为。

2 数值模拟

2.1 数值模型

为研究裂缝在不同性质的地层界面处的扩展行为，采用ABAQUS软件建立二维数值模拟模型如图4所示。模型尺寸为6m×3m，模型单元为平面四节点应力单元CPS4R。模型上下两部分为两种具有不同力学性质的岩层，厚度相等，均为1.5m。模型右侧施加6MPa的均匀拉力。模型上部的预制裂缝长度为0.5m。

图4 物理模型及尺寸Fig.4 Physical model and its dimension

2.2 应力强度因子的计算

裂缝尖端应力强度因子的求解方法较多，可分为解析法和数值法[19-20]，其中，数值法的应用较为广泛。应力强度因子的数值计算方法包括基于单元应力的外推法和基于节点位移的外推法。在有限元分析软件中，位移是求解的基本变量，其精度比应力高，因此，研究中采用基于节点位移的外推法来计算应力强度因子。

对于距离裂缝尖端r处，裂缝后端垂直位移u的数据可以在有限元软件中读取。根据I型裂纹尖端附近的位移场，裂纹面上的张开位移比较显著，采用θ=π时的裂纹张开位移值求解I型应力强度因子即

其中，E为弹性模量，ν为泊松比，κ为膨胀模量；对于平面应力问题，κ=(3-ν)/(1+ν)；对于平面应变问题，κ=3-4ν。

利用上式构造数据对(ri,KIi)，假设(ri,KIi)之间可用线性关系表示，用最小二乘法拟合数据点，所得直线截距即为所需计算的应力强度因子。

2.3 砂岩-泥岩界面裂缝扩展行为分析

2.3.1 岩石力学性质

数值模拟模型中，砂岩和泥岩的岩石力学参数见表1[1]。根据式(2)—式(4)分别计算得到α,β,λ以及界面强度系数χ如表2所示。从表中可以看出，当裂缝从砂岩向泥岩中扩展时，λ=0.455 0<1/2，χ=1.60>1而当裂缝从泥岩向砂岩中扩展，λ=0.553 2>1/2，χ=0.63<1。

表1 砂-泥岩模型中岩石力学性质参数Tab.1 Mechanical properties of rock in sandstone-mudstone numerical model

表2 砂-泥岩模型中裂缝扩展行为判别参数Tab.2 Judgment parameters for fracture extension behavior in sandstone-mudstone model

2.3.2 裂缝穿层扩展行为分析

裂缝由砂岩向泥岩穿层扩展过程中的Mises应力云图如图5所示。从图中可以看出，裂缝延伸初期，裂缝尖端距界面较远，界面对裂缝的延伸影响较小。随着裂缝尖端接近砂岩-泥岩界面，裂缝尖端出现应力集中，界面处出现明显的应力不连续现象。裂缝到达界面后穿过界面进入下部泥岩，并且延伸速度逐渐加快，直至贯穿整个模型。从裂缝扩展的整个过程来看，裂缝扩展方向稳定，从上部砂岩向下部泥岩扩展过程中，并未发生偏转或拐折现象。

图5 裂缝从砂岩向泥岩扩展过程中应力场变化Fig.5 Varying of stress field during fracture propagation from sandstone to mudstone

裂缝由泥岩向砂岩穿层扩展过程中的Mises应力云图如图6所示。裂缝扩展初期，裂缝尖端距界面较远，界面对裂缝的延伸影响较小。随着裂缝尖端与界面距离逐渐减小，裂缝尖端出现应力集中现象。当裂缝尖端距界面为0.25 m时，裂缝发生拐折，与界面斜交穿层进入下部砂岩层中继续扩展，直至裂缝贯穿整个模型。从裂缝扩展的整个过程来看，裂缝扩展初期方向稳定，随着裂缝尖端接近界面，裂缝发生拐折，拐折角度约为5.7°，裂缝拐折后穿层进入硬度较大的砂岩扩展。

图6 裂缝从泥岩向砂岩扩展过程中应力场变化Fig.6 Varying of stress field during fracture propagation from mudstone to sandstone

2.3.3 应力强度因子变化

为观察裂缝扩展过程中应力强度因子的变化情况，采用上文所述方法，计算当裂缝尖端距离界面1.0 m、0.75 m、0.5 m、0.25 m、0 m(裂缝长度为0.5 m、0.75 m、1.0 m、1.25 m、1.5 m)时裂缝尖端的I型应力强度因子，结果如图7所示。对于裂缝从砂岩向泥岩扩展的情况，裂缝开裂后，裂缝尖端应力强度因子逐渐增大，达到约8 MPa·m1/2后，裂缝平稳扩展。随着裂缝尖端逐渐接近砂岩-泥岩界面，I型应力强度因子迅速增大，使裂缝加速穿层，从上部砂岩中进入下部泥岩中扩展。

图7 砂-泥岩模型中裂缝尖端接近界面时应力强度因子变化Fig.7 Varying of stress intensity factor when crack tip approaches interface in sandstone-mudstone model

对于裂缝从泥岩向砂岩扩展的情况，裂缝扩展初期与裂缝从砂岩向泥岩中扩展相似，裂缝起裂延伸后，裂缝尖端应力强度因子逐渐增大，达到约7 MPa·m1/2后，裂缝向下部延伸，裂缝长度逐渐增大。随着裂缝端部与泥岩-砂岩界面的距离的减小，裂缝尖端应力强度因子逐渐降低，裂缝穿层扩展的趋势受到限制。在裂缝尖端到达界面前，裂缝已发生拐折现象。

2.4 煤层顶板-煤岩界面裂缝扩展行为分析

2.4.1 岩石力学性质

数值模拟模型中，煤层顶板和煤层的岩石力学性质根据陕西彬县4号煤相关参数进行设置[3]，具体数值如表3所示。根据式(2)—式(4)分别计算得到α,β,λ以及界面强度系数χ如表4所示。从表中可以看出，当裂缝从煤层顶板向煤层中扩展时， λ=0.340 7<1/2， χ=5.90>1， 而当裂缝从煤层向顶板粉砂岩中扩展时，λ=0.6956>1/2，χ=0.17<1。

表3 煤层-顶板模型中岩石力学性质参数Tab.3 Mechanical properties of rock in roof-coal rocknumerical model

表4 煤层-顶板模型中裂缝扩展行为判别参数Tab.4 Judgment parameters for fracture extension behavior in roof-coal rock model

2.4.2 裂缝穿层扩展行为分析

裂缝从顶板(粉砂岩)向煤层穿层扩展过程中的Mises应力云图如图8所示。从图中可以看出，裂缝从上部粉砂岩中起裂后，沿原方向向下扩展，到达并穿过界面后进入煤层，直至贯穿整个模型。在裂缝扩展的整个过程中，裂缝扩展方向稳定，并未发生偏转或拐折现象。

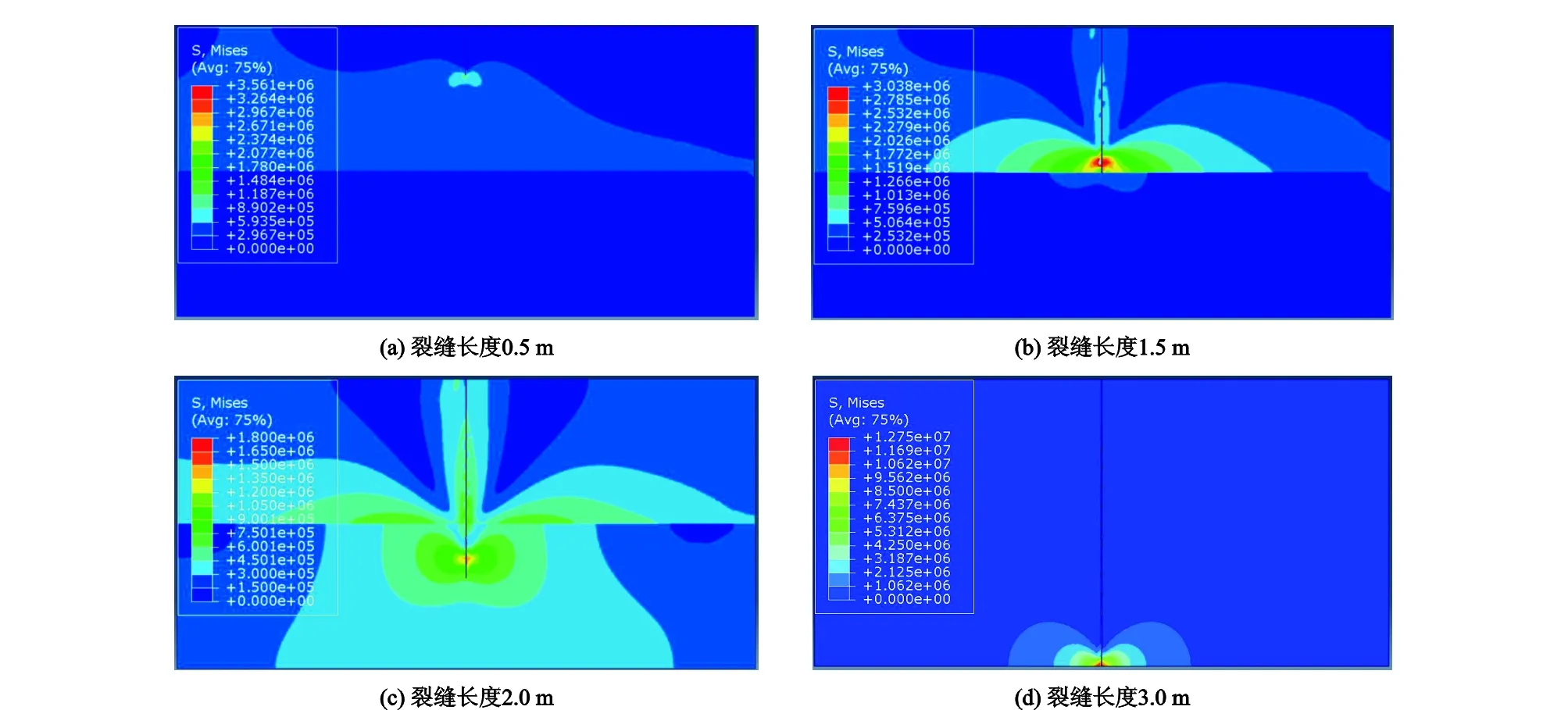
图8 裂缝从顶板向煤层扩展过程中应力场变化 Fig.8 Varying of stress field during fracture propagation from roof to coal rock

裂缝由煤层向粉砂岩扩展过程中的Mises应力云图如图9所示。从图中可以看出，裂缝起裂后立即向模型右侧偏转，当裂缝尖端到达界面时与界面斜交，夹角约为45°。随后裂缝沿该角度穿层延伸进入下部粉砂岩中，在砂岩中裂缝尖端距界面距离0.6 m处，裂缝发生第二次转向并向模型底部扩展，直至贯穿整个模型。裂缝扩展过程表明，裂缝扩展初期即发生明显的拐折现象，偏转角度最大可达45°，界面两侧岩石力学性质差异对裂缝的穿层延伸过程产生了较大的影响。

2.4.3 应力强度因子变化

为观察裂缝扩展过程中应力强度因子的变化情况，计算当裂缝尖端距离界面1.0 m、0.75 m、0.5 m、0.25 m、0 m(裂缝长度为0.5 m、0.75 m、1.0 m、1.25 m、1.5 m)时裂缝尖端的I型应力强度因子，结果如图10所示。对于裂缝从粉砂岩向煤层中扩展的情况，裂缝从粉砂岩中起裂后，应力强度因子逐渐增大，当裂缝长度由0.75 m增大至1.0 m的过程中，裂缝在粉砂岩层中稳定扩展，裂缝尖端应力强度因子变化不大。随着裂缝尖端逐渐接近界面，应力强度因子急剧增加，裂缝加速穿层扩展。对于裂缝从煤层向粉砂岩扩展的情况，应力强度因子较为稳定，整体呈现先增加后缓慢下降的趋势。从裂缝扩展过程可知，裂缝在穿层扩展前已发生明显的拐折现象，裂缝尖端接近界面时，界面强度因子降低，不利于裂缝穿层扩展。

图9 裂缝从煤层向顶板扩展过程中应力场变化Fig.9 Varying of stress field during fracture propagation from coal rock to roof

图10 煤层-顶板模型中裂缝尖端接近界面时应力强度因子变化Fig.10 Varying of stress intensity factor when crack tip approaches interface in roof-coal rock model

3 实例应用

某煤层气水平井位于煤层顶板中，拟通过水力压裂的方式与下部煤层实施沟通，其工程模型如图11所示。水力压裂裂缝从煤层顶板起裂后能否沟通下部煤层，形成有效的产气通道，是技术成功的关键，因此需要判断水力压裂裂缝在煤层顶板和煤层界面处的穿层行为。煤层及其顶板的岩石力学参数见表5，利用研究成果，计算得到裂缝从煤层顶板(泥岩)向煤层中扩展时的相关参数如表6所示。从表中可以看出，当裂缝从煤层顶板向煤层中扩展时，λ=0.4834<1/2，χ=1.22>1。根据上述结论，当裂缝从顶板起裂后到达煤层顶板和煤层的界面处时，可沿原路径顺利穿层扩展，进入煤层，从而沟通水平井井筒与煤层，为煤层气进入井筒提供通道。

图11 顶板压裂裂缝延伸示意图Fig.11 Schematic diagram for extension of fracture in fracturing of roof horizontal well

岩性抗拉强度/MPa弹性模量/GPa剪切模量/GPa泊松比煤层顶板(泥岩)0.56010.304.080.31煤层0.0697.202.730.40

表6裂缝穿层行为判别参数Tab.6 Judgment parameters for fracture extension behavior from roof (mudstone) to coal seam

为观察水力压裂裂缝形态，判断裂缝在纵向上的延伸情况，该水平井在实施分段压裂时，对其中2个压裂段进行了微地震监测。钻井数据表明，水平井井筒距下部煤层顶部距离为0.5～1.5 m。微地震监测数据分析表明，煤层及其顶板中均有较多的微地震事件，解释得到的压裂裂缝高度分别为20.5 m和17.6 m，证明裂缝实现了穿层扩展，沟通了水平井井筒和煤层，为煤层气进入井筒提供了通道。

4 结 论

(1)界面两侧岩石力学性质差异对裂缝的穿层延伸具有影响。

(2)由岩石力学性质差异决定的界面强度系数可用于判断裂缝的穿层扩展行为。当界面强度系数大于1时，裂缝可沿原路径顺利穿层扩展；当界面强度系数小于1时，裂缝的穿层行为将受到影响，裂缝可能停止扩展或拐折穿层扩展。

(3)当裂缝从高强度岩层起裂向低强度岩层扩展时，裂缝扩展方向稳定，裂缝扩展角度基本不变，裂缝尖端应力强度因子随着裂缝尖端与界面距离的减小迅速增大；当裂缝从低强度岩层起裂向高强度岩层扩展时，裂缝在到达界面前发生偏转，且界面两侧岩石力学性质差异越大，裂缝偏转角度越大，裂缝尖端应力强度因子随着裂缝尖端与界面距离的减小逐渐减小。