裂缝性油藏注水井动态渗吸数学模型及特征分析

2019-02-13李蒙蒙林加恩

西安石油大学学报（自然科学版） 2019年1期

李蒙蒙，李琪,，林加恩，毕刚

(1.中国石油大学(北京) 石油工程学院，北京 102249；2.西安石油大学石油工程学院，陕西西安 710065)

引言

在20世纪50年代，美国Spraberry砂岩油田发现渗吸采油是裂缝性油藏采油的重要机理。1958年，Aronofsky等人[1]将饱和油样的岩心浸没在纯水中，经过一段时间后计算渗吸累采油量，提出了经典的指数型渗吸经验公式。后来有许多学者应用此经验公式计算裂缝与基质之间的窜流量。1978年，De Swaan[2]考虑裂缝中含水饱和度的变化，基于裂缝中水的体积守恒，提出了卷积形式的渗吸经验公式。1992年，Kazemi等人[3]基于De Swaan提出的渗吸经验公式，得到了裂缝性油藏一维Buckley-Leverett 流动方程，并进行了解析和数值求解。后来也有一些学者[4-9]考虑渗吸作用，建立了一维油水两相渗流数学模型，但多是基于单个基质岩块进行的流动分析。国内也有许多学者对裂缝性油藏油水两相驱替过程中渗吸作用进行了研究，陈钟祥[10]、郭大立[11]等人基于Aronofsky渗吸经验模型，应用特征线法对双重孔隙介质油水两相驱替方程进行求解，分别得到了方程的近似解析解和精确解。邓英尔[12-13]基于扰动椭圆的概念，分别建立了双重孔隙介质油藏垂直裂缝井和水平井的油水两相流动渗流数学模型并进行了数值求解。但应用数值方法[14-17]分析裂缝性油藏水驱变化规律存在计算量大、数值弥散等问题。本文在前人研究基础上，建立了两种裂缝性油藏注水井动态渗吸数学模型，并应用Laplace变换与Laplace 反演算法进行解析求解，分析了裂缝性油藏的动态渗吸特征。

1 注水井物理模型

裂缝性油藏中心有一口注水井定注入量进行注水，将油藏分成三个区域。其中一区为高含水区域，二区为油水两相过渡区，三区为注入水未波及的具有原始含油饱和度的油区。裂缝性油藏分别采用双孔单渗模型和双孔双渗模型两种模型进行描述。储层厚度不变，流体为微可压缩流体，在裂缝与基质系统中的流动符合达西定律。基质与裂缝之间存在窜流，且流动为拟稳态流动。裂缝性油藏注水井物理模型示意图，见图1。

2 注水井渗吸数学模型

裂缝性油藏在注水过程中，注入水首先进入裂缝，驱替裂缝中的原油。

图1 裂缝性油藏注水井物理模型Fig.1 Physical model of water injection well in fractured reservoir

此时，基质周围的裂缝中充满水，在毛管力的作用下，水从裂缝进入基质，通过渗吸作用，将基质中的原油驱替到裂缝中。Arnofsky假定被水包围的基质岩块的累积采油量是关于时间的连续单调函数并且收敛于一极限值，得到了裂缝性油藏累积采油量与时间的指数型经验公式[1]

R=R∞(1-eRct)。

(1)

其中：

R∞=φm(1-Sorm-Swcm)，

(2)

R=φm(Swm-Swcm)。

(3)

式中：R为采收率，%；Rc为渗吸强度系数，1/d；R∞为最终累积采出程度，%；φm为基质系统孔隙度，%；t为时间，h；Sorm为基质系统残余油饱和度，%；Swcm为基质系统束缚水饱和度，%；Swm为基质系统含水饱和度，%。

Arnofsky的指数型经验公式是在静态渗吸的条件下得到的，而在注水过程中，裂缝性油藏基质周围的裂缝中含水饱和度是不断变化的。基于此，De Swaan考虑裂缝中含水饱和度变化，提出了新的积分形式的渗吸经验公式[2]

(4)

式中：qm为渗吸采收率，%；Swf为裂缝系统中的含水饱和度，%。

下面根据此渗吸经验公式，分别建立双孔单渗模型和双孔双渗模型的径向水驱油Buckley-Leverett(B-L)方程[18]，并通过Laplace变换与反演算法得到解析解。

2.1 双孔单渗油藏渗吸数学模型

双孔单渗模型即为Warren-Root模型，模型中存在相互正交的基质系统和裂缝系统。裂缝系统作为流体的流动通道，注入水进入地层以后，首先驱出裂缝中的原油，此时裂缝中的含水饱和度上升。由于毛管力渗吸作用，注入水进入基质岩块，排驱其中的原油。忽略基岩系统内部的流动，基质系统看作向裂缝系统补给的“源”。根据裂缝中的体积守恒，结合一维水驱油B-L流动方程和渗吸经验公式，得到双孔单渗油藏径向流动B-L方程[19-20]。

裂缝系统：

(5)

基质系统：

(6)

初始条件：

Swf(r,t=0)=0。

(7)

边界条件：

Swf(r=0,t)=1。

(8)

式中：q为日注水量，m3/d；h为储层厚度，m；r为径向距离，m；rw为井径，φf为裂缝系统孔隙度。

引入Laplace变量z1，对式(5)、式(6)和式(8)进行Laplace变换并代入初始条件可得

(9)

(10)

(11)

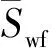
通过积分求解，并代入边界条件可得Laplace空间中裂缝与基质系统的含水饱和度变化公式

(12)

(13)

其中：

(14)

(15)

通过拉普拉斯反演，可以得到实空间中基质与裂缝系统中含水饱和度变化公式：

(16)

(17)

2.2 双孔双渗油藏渗吸数学模型

双孔双渗模型是在Warren-Root模型的基础上，考虑了基质系统中流体的流动。即当注入水进入地层以后，流体同时进入基质系统与裂缝系统中，但由于裂缝系统渗透率大于基质系统，所以裂缝中水的推进速度要快于基质系统中水的推进速度。由于毛管力渗吸作用，裂缝系统中的水进入基质岩块，排驱其中的原油，从而抑制裂缝中水的突进。双孔双渗模型基质系统的渗流控制方程在双孔单渗模型的基础上添加了流动项。根据裂缝中的体积守恒，结合一维水驱油B-L流动方程和渗吸经验公式，得到双孔双渗油藏径向流动B-L方程。

裂缝系统：

(18)

基岩系统：

(19)

初始条件：

Swf(r,t=0)=0，

(20)

Swm(r,t=0)=Swcm。

(21)

边界条件：

Swf(r=0,t)=1，

(22)

Swm(r=0,t)=1。

(23)

引入Laplace变量z1，对式(18)、式(19)、式(22)和式(23)进行Laplace变换并代入初始条件可得

(24)

(25)

(26)

(27)

通过积分求解，并代入边界条件可得Laplace空间中裂缝与基质系统的含水饱和度变化公式

(28)

(29)

通过拉普拉斯反演，可以得到实空间中基质与裂缝系统中含水饱和度变化公式：

(30)

(31)

3 裂缝性油藏渗吸特征分析

根据裂缝性油藏注水井渗吸数学模型得到的解析解，使用MATLAB软件编程可得到注水井注水过程中基质与裂缝系统中的含水饱和度变化规律，从而分析渗吸作用对水驱油效果的影响。图2和图3反映了双孔单渗模型注水井动态渗吸特征，图4和图5反映了双孔双渗模型的注水井动态渗吸特征，应用渗吸数学模型计算注水过程中的饱和度值，所使用的参数如表1所示。

表1 裂缝性油藏饱和度分布计算参数Tab.1 Parameters for calculation of water saturation distribution in fractured reservoir

图2和图3为注水井注入100 d后，渗吸强度系数分别为0, 0.001, 0.01, 0.1 和1时，双孔单渗油藏裂缝系统和基质系统中的含水饱和度分布图。通过两图对比可以看出，当渗吸强度系数为0，即不考虑渗吸时，水在裂缝中的驱替过程相当于活塞式驱替，裂缝水淹较快，水驱替过后裂缝中含水饱和度达到最大含水饱和度值。在驱替前沿处，含水饱和度存在一个突变。基质中的含水饱和度基本没有发生变化，含水饱和度值为束缚水饱和度。表明当不考虑渗吸时，注入水沿裂缝突进，只能驱替出裂缝中的原油，基质中的原油基本不能被采出，驱油效果较差。

从图3可以看出，当渗吸强度系数不为0时，注入裂缝中的水会通过毛管力渗吸作用进入基质，基质中的原油被驱替到裂缝中，从而抑制裂缝中水的突进，使裂缝中含水上升变缓。在油水界面处含水饱和度没有发生突变，而是逐渐缓慢的变化，存在油水过渡带。随渗吸强度的增加，油水两相区的扩大速度变慢，含水上升速度变缓，裂缝中的水能够充分进入基质，驱替出更多的原油。裂缝中的原油主要靠水的驱动作用采出，而基质中的原油主要靠毛管力渗吸作用驱出。表明对于裂缝性亲水油藏，毛管力渗吸作用是水驱油的主要动力。

图4和图5为当渗吸强度系数分别为0.01和1时，注入时间分别为5，50，100，200，300 d时，双孔双渗油藏基质与裂缝系统中的含水饱和度变化曲线。两图对比可以看出，当渗吸强度系数较小(Rc=0.01)时，随注入时间的增加，油水两相区的范围逐渐变大，水驱前沿在裂缝与基质系统中的推进速度基本一致。这是由于当渗吸强度系数较小时，裂缝中的水虽然会进入基质，但是基质与裂缝中的流体作用不够充分，基质中只有部分原油被驱出，所以油水两相区的范围会变大。

图2 不同渗吸强度系数条件下裂缝系统中的含水饱和度分布Fig.2 Water saturation distributions in fracture system under different imbibition intensity

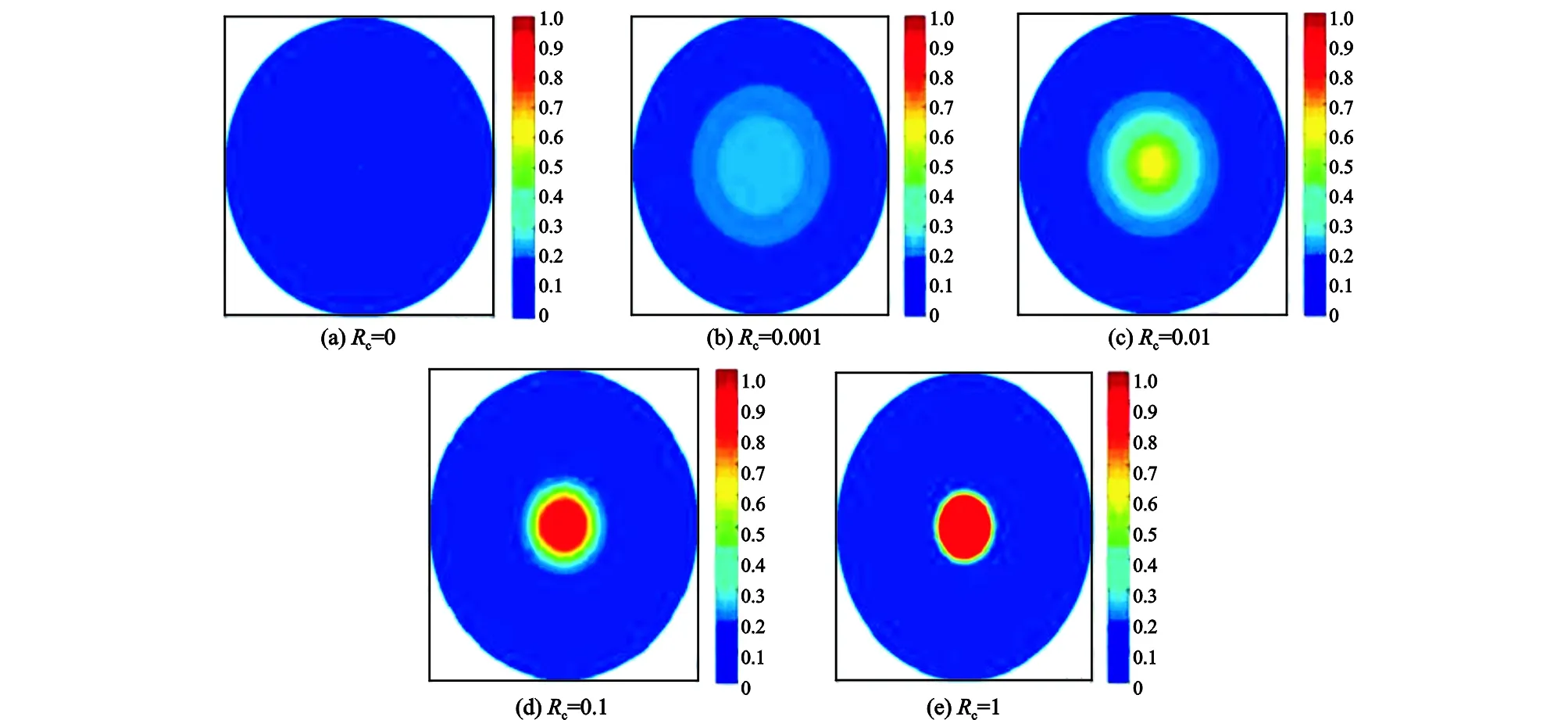
图3 不同渗吸强度系数条件下基质系统中的含水饱和度分布Fig.3 Water saturation distributions in matrix under different imbibition intensity

图4 渗吸强度系数为0.01时基质系统和裂缝系统中的含水饱和度变化曲线Fig.4 Varying curves of water saturation in matrix and fracture with distance when Rc=0.01

图5 渗吸强度系数为1时基质系统和裂缝系统中的含水饱和度变化曲线Fig.5 Varying curves of water saturation in matrix and fracture with distance when Rc=1

从图5可以看出，当渗吸强度系数较大(Rc=1)时，随注入时间的增加，水驱前沿在基质和裂缝中的推进速度基本一致，油水两相区的范围相比渗吸强度系数为0.01时变小。这是由于随渗吸强度系数的增加，裂缝中的水能够充分进入基质，使裂缝与基质中流体交换更加充分，驱替出更多的原油。因此，当渗吸强度系数为1时，水驱前沿在基质和裂缝中的推进速度比渗吸强度系数为0.01时的推进速度变缓。