康熙朝经线每度弧长标准的奠立——兼论耶稣会士安多与欧洲测量学在宫廷的传播

韩 琦 潘澍原

(1.中国科学院大学人文学院，北京 100049； 2.中国科学院自然科学史研究所，北京 100190)

明清之际西学输入以崇祯(1628—1644)和康熙(1662—1722)两朝为最，而后一时期高潮迭起，精彩纷呈，更为引人注目。康熙帝出于个人爱好和权术考量，躬身向耶稣会士学习，(1)关于康熙帝西学研习与其治术之关系，参见文献[1—4]。数学、天文、地理、物理、乐律、医药等知识因而得以传入宫廷。作为康熙朝最大的科学工程，大地测量和舆图绘制最为史家所关注。一般认为，这一工作始自康熙四十七年(1708)，至五十七年(1718)告成。然而，康熙帝此前已陆续派员开展测量活动，耶稣会士和皇子都参与其中，为后续全国范围的大规模舆地测绘奠定了基础。本文将结合中西史料和文献，以耶稣会士安多(Antoine Thomas， 1644—1709)(2)关于安多的生平和科学活动，参见文献[5—6]。关于安多在华期间的地图测绘和数学、天文工作，参见文献[7—14]。的相关活动和著作为中心，阐述其所从事的测量实践及其背景，并揭示当时宫廷数学传播的特点和数学著作译撰的复杂情形。

1 明季欧洲测量学知识的传入

测量学在中国源远流长，古代算学以“测望”名之，有“句股”“重差”等类别。(3)中国测量学发展的早期考述，参见文献[15]。《周髀算经》首篇和《九章算术》句股章皆有利用相似直角三角形边长关系推求高深广远的测量知识。利用两表测算日高的“重差”方法，至迟在汉代即已现世。曹魏末年，刘徽撰作《重差》(后称《海岛算经》)，完善其术。唐李淳风(602—670)等注释《周髀》，将“重差”推广至斜面立表。宋秦九韶(1208—约1261)《数书九章》(1247)以“测望类”专作一章，亦有发明。元中期以后，测量学知识渐趋普及和实用化。晚明程大位《算法统宗》(1593)“海岛题解”以下诸题[16]设问浅近，歌诀、图示简捷明了。

作为实用几何学的主要内容之一，欧洲测量学(4)关于欧洲的实用几何传统及测量学在其中的地位，参见文献[17—19]。在明末传入中国，经耶稣会士利玛窦(Matteo Ricci， 1552—1610)等人的演示与教授([20]，页5；[21])，很快引起士人的兴趣，成为经世济民的实学课题。万历三十五年(1607)《几何原本》刊印稍后，徐光启(1562—1633)与利氏合作编译晚明首部测量学专论《测量法义》(约1610出版)，主要目的之一就是要“广其术而以之治水、治田之为利巨、为务急也”([22]，题测量法义，页1)。崇祯二年(1629)改历之初，徐光启在条陈修历内容、人员、仪器之外，更提出“度数旁通十事”，期望借此将数学知识应用到关乎国计民生的各方面：

度数既明，可以测量水地，一切疏濬河渠、筑治堤岸、灌溉田亩，动无失策，有益民事。……天下舆地，其南北东西、纵横相距、纡直广袤，及山海原隰高深广远，皆可用法测量，道里尺寸，悉无谬误。([23]，页337—338)

均属测量学的应用。随后徐光启、李之藻(1565—1630)与耶稣会士罗雅谷(Giacomo Rho， 1593—1638)等人合作译撰《测量全义》(1631)，(5)《测量全义》崇祯三年(1630)九月已成二卷，“系臣光启、臣之藻同陪臣罗雅谷译撰”([23]，页348)。其卷二、三“测线”([24]，测量全义叙目，页6)专述大地测量，方法、仪器及理论基础等均较《测量法义》全面。(6)徐光启的学生孙元化(1581—1632)亦曾在兵书《西法神机》中介绍以欧式仪器测量敌营目标距离的方法，参见文献[25]，页38—40。

明季介绍的测量方法不外两种。一是利用相似直角三角形直角边对应关系，量取所需长度或比例长度，按比例推算；二是构建包含所求对象在内的平面三角形，量取相关角度和长度，并利用三角函数线长度按比例推算。复杂情况时需多次测量和计算。测量仪器主要有矩度(geometric square)和象限仪。象限仪用以测角，《测量全义》对其配备窥衡或垂线的不同形制和其“平安”“侧置”两种使用方式有详细解说([24]，卷3，页6—8；卷2，页1，27)。矩度形为正方板，相邻两边作同等的均匀划分，形成纵横等长而设有分度(比例长度)的直影和倒影，亦使用垂线或窥衡，即《测量法义》所示垂悬式([22]，页1—2)和《测量法义》所示固定式([24]，卷3，页9)。矩度亦称度高标尺(scala altimetra)，常以简化形式影矩(shadow square)附于其他仪器之上，[26]《测量全义》“造矩度法”之“约法”([24]，卷3，页9)，即介绍如何在象限仪弧内附设矩度，因而兼具分度与角度测量两种功能。(7)关于晚明自欧洲引入的大地测量仪器的详细考察，参见文献[27]。

2 康熙帝的测量学研习与实践

相较晚明的社会需求与实学氛围，康熙时代测量学知识的传播有着更为直接的缘由。康熙三至八年间(1664—1669)，杨光先(1597—1669)掀起的反教案给尚在冲龄的康熙帝带来极大触动，成为其历算研习的原始动因。此后他便亲自向耶稣会士南怀仁(Ferdinand Verbiest， 1623—1688)求教，学习数学仪器的使用和几何学、静力学、天文学等知识([28]，页123—124)。1675年5月起，康熙进行了集中而系统的研习([29]，页98，263)，在了解欧几里得几何学、三角学之后，又“以极大的乐趣转向更为令人愉悦的问题上，亦即实用几何学、测地学、区域地图绘制学(Chorography)及其他引人兴味的数学科学”，并期望这些知识能够“当面演示和验证”([29]，页99—100)。为此，他在观象台设置测天六仪以外，“命造内廷备用测天诸器，如黄赤二道、天体星球、圭表，并测地高低远近等项之仪器”([30]，页129)，时常操作象限仪、十字杆(radios astronomicos)、矩度、经纬测角仪(pantometra)等测量仪器([29]，页100，404)(8)“矩度”依南怀仁原书“quadrata geometrica”译出。，并用作实测：

他用仪器测量物体的高度和长度，并绘制区域地图，当看到他的计算如此接近于事物的真实情况和两地之间的实际距离时(因为没有充分的自信，他随即就用量竿和绳索对此加以检验)，就非常高兴。([29]，页100)

这样的“演示与验证”，显然令康熙对实用几何知识和测量仪器的功用印象深刻。

在数学知识之外，康熙对西方地理、风物也颇感好奇，特别是通过南怀仁等编制的《御览西方要纪》(1669)和《坤舆全图》(1674)大大扩展了知识视野，同时更因军事、河流等治理之需，对地图绘制日益关注。二十五年(1686)，《大清一统志》开编之时，他谕示修纂方针，要求将大清疆域山川等“质订图经”“画地成图”，并称“万几之余，朕将亲览”([31]，卷126，册5，页342—343)。

康熙二十七年(1688)初，洪若(Jean de Fontaney， 1643—1710)、张诚(Jean-François Gerbillon， 1654—1707)、白晋(Joachim Bouvet， 1656—1730)等“国王数学家”到达北京，进呈法国国王路易十四(1638—1715)赠送的各类科学仪器、书籍等礼物三十箱，其中有“西洋地理图五张”([30]，页169)。此后张诚、白晋留在北京，成为御用教师。1690—1691年间，他们频繁进出宫廷，讲授数学、哲学和医药知识，康熙的西学研习达至高潮。1690年3月上旬，张诚、白晋开始向康熙讲解欧几里得《原本》的命题；3月下旬，由于康熙希望尽快知道最为必要的几何命题，以求理解此前已有所接触的实用几何学，两人选用法国耶稣会数学家巴蒂斯(Ignace-Gaston Pardies， 1636—1673)简单明了、易于理解的《几何原本》(Elemensdegeometrie)作为教材，并编译为满文和汉文([32]，页228，245；[28]，页144)。事实上，注重实用正是巴蒂斯书的一大特点，其末卷“问题，或实用几何”(Problems， ou la Geomerie pratique)的诸多例题也被译出，其中就有运用仪器测绘地形的方法(图1)[33—34]。

图1 《几何原本》所示“用仪器画地形图法”及法文原著对应图示([34]，页67；[33]，页107)

与此同时，康熙也积极将几何学付诸实践，尤其热衷于测量仪器的操作。1690年1月15日，康熙要求张诚等耶稣会士“次日早晨将其住处其他适用于测量地点高度和距离及测取星体距离的仪器带去”；16日，张诚等呈上仪器，康熙对路易十四之子梅恩公爵(Louis-Auguste de Bourbon， Duc du Maine， 1670—1736)所赠半圆仪的精准性称赞有加，要求张诚讲解其功能和使用，并和他们一起演练([32]，页218—220)。白晋曾描述康熙对该仪的青睐和使用：

在这个时候，我们必然是把我们住处但凡适合他使用的都呈献给他。其中一件承梅恩公爵先生好意赠与我们，是一座精美硕大且带有窥衡镜片的半圆仪，很适于进行几何操作。除平日在宫廷御花园使用它外，旅途中他也让一名内府官员背着它到处随行，尽管因为背上这一珍贵包袱的重量而行动不便，但这位官员并不因此而感到不体面。他经常使用它，有时是测量某座山的高度，有时是一些引人注目的地点之间的距离，这一切都是在整个朝廷众目睽睽之下。令众人惊异的是，他们的皇帝在进行这些操作时都很成功，与每次旅行都照例伴驾的耶稣会士张诚神父一样。([28]，页137—138)

显然，康熙完全掌握了基于三角学的测量方法。张诚的扈从日记则披露了更为生动的细节。(9)博西耶尔夫人依据张诚日记择要概述其八次随行经历([35]，页29—92)，涉及测定某地纬度、测量高远、绘制地图、协助皇帝研习几何学和使用仪器等，所述均较为简略。如1691年4月20日，康熙召见张诚，希望他下月随驾前往鞑靼地区，并协助进行利用几何学的测量工作，不久张诚便随同康熙北巡([32]，页251—252)。6月6日(三十年五月初十日)，康熙“驻跸超射峰南”([36]，册2，页761)，张诚记述，皇帝射箭超过峰顶：

随后他命我用他带来的仪器测量那块岩石的高度。他携带了一件半径半法尺(pied)的半圆仪，它只能用小孔从较远的基点来观测。观测完成之后，他想要我们各自分别计算那块岩石的高度；我们得到结果为四百三十尺(Ché)即中国尺。第一次观测后，他仍想对同一块岩石高度再作一次观测，但基点建立在更远的地方。我们当着所有大人的面各自进行推算，他们不禁称赞那些推算是如此一致，数字无一不同；而皇上为了使他们信服，让我一一读出我的两份推算，同时向那些老爷出示他自己的，他们则不断惊叹其精确。皇帝还用几何方法测量了一段距离，在计算并公布结果后，他又命人实地丈量，其结果与计算正相吻合。([32]，页282)

可见康熙学习测量颇有成效，并重视实际用途，还时常以此炫学于群臣，令其折服。

3 耶稣会士安多与大地经线1度弧长的测定

在初步研习测量学之后，康熙帝在出巡途中经常亲身实践，亦经常遣员实测，耶稣会士安多便是这些活动的主要人物之一。安多生于今比利时纳慕尔(Namur)，早年在耶稣会学院学习，1679—1680间年任教葡萄牙科因布拉(Coimbra)耶稣会学院，期间编成《数学纲要》(SynopsisMathematicacomplectensvariostractatusquoshujusscientiaetyronibusetMissionisSinicaecandidatisbreviteretclareconcinnavitP.AntoniusThomasèSocietateIesu， Duaci， 1685)，旨在为初学者和将要前往中国的传教士提供算术、几何、球面三角、天文、地理、力学、光学、音乐、钟表等门类的简要知识(10)关于该书的缘起、内容、编撰、出版、影响及阅读史的考察，参见文献[37]。。1680年，他从里斯本登船前往印度，1682年7月抵达澳门。康熙二十四年(1685)初，南怀仁年老体弱，需要助手，安多因较高的数学水准而应召，十月到京陛见，入钦天监工作([30]，页157，158)。

1690年初，安多帮助康熙复习南怀仁之前教授的几何、算术和仪器知识([28]，页126—127；[32]，页282)；后来将《数学纲要》的部分内容编译为《算法纂要总纲》，又编写《借根方算法》《借根方算法节要》，向康熙讲授算术、实用几何学和代数学知识([11]，页150—153；[10]，页108—113)。同时，在钦天监负责“天文历法、五星凌犯、日食月食事”([30]，页170)，还曾向来京纂修《明史·历志》的黄百家(1643—1709)传播哥白尼(Nicholas Copernicus，1473—1543)的日心说([12]，页55—57；[14]，页71—73)。三十六年(1697)，康熙征讨噶尔丹期间，安多随行至宁夏，测验闰三月初一日(4月21日)日食([6]，页84；[38]，页249—250)。初五日，康熙谕留守京师的皇太子胤礽(1674—1725)：

朕至此地，即以仪器测验，较之京城北极低一度二十分，东西远二千一百五十里。以此付安多照法推算。原谓日食九分四十六秒，乃是日大晴，测验之，食九分三十几秒，并不昏黑见星。自宁夏视京师，在正东而稍北。([39]，卷40，页32—33)(11)康熙《御制文第二集》收有同一谕旨([40]，卷24，页13)，措词略有差异，参见文献[41]，页184。

并令其寄告京城日食时刻情形。初七日，胤礽回奏钦天监用仪器测得结果，又据自身观测称“食不至十分”，康熙朱批“安多与朕亦议，观此地日食情状，即断言京城未必全食，约余数秒，果然应验”[42]，透露出对安多的赞赏和信任。

除传授数学和天文测算之外，安多也承担了许多测绘工作。二十四年到京后不数日，安多便收到康熙让他绘制鞑靼地图的要求([6]，页67)。(12)1689年《尼布楚条约》签订以后，安多曾绘制两幅亚洲地图寄往罗马，参见文献[8]，页83—84。三十七年(1698)三月，直隶巡抚于成龙(1638—1700)等“奉使往视浑河、清河”测量河道([36]，册11，页6279—6281)，十六日“以浑河图形呈览”，奏称：

臣同西洋安多等自霸州入定河一道，自卢沟桥起至霸州药王庙止，尚可由水路丈量。自霸州堤乘马至苑家口，乘船至信安，由信安至丁字沽，看至里郎城，履旧河形，一路丈量到永清、固安。([36]，册11，页6298—6299)(13)同日《实录》记载([31]，卷187，册5，页996)较所引《起居注》稍略，参见文献([9]，页102)。

可见安多全程跟随于成龙前往霸州等地测量河道形势，绘制成图。(14)当年七月于成龙疏言“霸州等处挑濬新河已竣”，康熙赐名“永定河”([31]，卷189，册5，页1007)。值得指出的是，此前康熙曾数至霸州视察浑河、清河，之后三十八至四十一年间，更是每年皆至霸州一带巡视河堤([36]，册14，页7487—7496，7782—7786，7933—7935；册15，页8511，8514，8519—8520；册17，页9248—9250)。三十七至三十八年间(1698—1699)，安多还受命前往南直隶绘制黄河图形([6]，页67—68)。(15)康熙四十一年(1702)，安多还曾前往俄罗斯馆索取俄国地图，然未能获得，事见文献[43]。

在讨论安多测量大地经线1度弧长的工作(16)翁文灏、李约瑟等([44]，页4；[45]，页27；[46])曾述及康熙朝舆地测绘以安多所测经线每度里数为标准。之前，我们先简单回顾相关背景。希腊化时期数学家埃拉托色尼(Eratosthenes，约前276—前195)根据地圆学说和日影观测估算周长、每度弧长、半径等地球尺度，之后学者屡有改订。唐代中土虽无地圆观念，僧一行等亦通过实测和校算得出北极出地高度差1度而南北相距351里80步，实与经线每度弧长相当。[45]晚明地圆说自欧洲输入，传教士皆以中国里数给出大地每度弧长，或因换算误差，数值不尽相同([47]，页37—38；[48]，页172，174；[49])。万历二十六年(1598)南京刊印《山海舆地全图》之际，利玛窦重新设定地球每度为250里([50]，页37—38；[51]，页21—22)(17)关于南京所刻《山海舆地全图》的年份，参见文献([52]，页307)。，尔后《乾坤体义》《浑盖通宪图说》《表度说》《简平仪说》及《天问略》《职方外纪》《崇祯历书》等西学著作，以及南怀仁《坤舆图说》(1674)均沿袭此值。

康熙帝曾于三十五年(1696)行军途中测定喀伦北极高度与京师相差5度，认为“以此度之，里数乃一千二百五十里”([39]，卷22，页33；[40]，卷19，页7)，(18)参见文献([41]，页184)。仍从1度250里之说；及至1698年12月查看西鞑靼地图，发觉按纬度推算的距离与此前实测不符，遂向安多咨询缘由。1702年冬南巡期间，他委派皇三子胤祉(1677—1732)携领人员实施测量，安多作为这次活动的主持者，将详细经过写成《关于1702年12月在中国直隶进行的地球一度的测量》(De dimensione unius gradus Orbis Terrae Factain Prov(incia) Pekinensi Regni Sinarum Anno 1702， Mense Decembri)的专题报告寄往欧洲([5]，tome 46，页154—181；[6]，页111—114；[9]，页92—100)(19)报告节译参见本文附录。。

在此稍前，欧洲已有类似的大地测量活动。其中法国天文学家、测地学家皮卡尔(Jean Picard，1620—1682)的工作最为重要。作为1666年皇家科学院的创始成员，皮卡尔于1668—1670年间为科学院主持测量Sourdon和Malvoisine两地间的经线弧长以获得更为精确的地球半径值，后将这次测量的仪器、方法、经过等汇集在《地球测量》(Mesuredelaterre， 1671)一书[53]中出版。在测量之前，他首次为象限仪等测角仪器配备望远镜，这一革新大大提高了观测的准确性。他以13个大三角形组成的三角测量网得出两地的间距，并根据起讫点纬度差推算大地经线1度弧长为57060笃亚斯(toise)，由此导出的地球半径曾被牛顿(Isaac Newton，1643—1727)用于验证其地心引力理论[54—55]。

1702年11月中旬，胤祉派员在北京周边寻找适合测量的平原地域，最终选定在顺天府霸州至河间府交河县之间。12月2日从霸州城外开始，以长度为1标准里的铁线逐里丈量，并设桩立杆，以仪器窥望相准，确保其沿经线方向连续取直。如此量取200里，全程基本在同一经线之上。随后测量南北两端北极高度及正午太阳高度、日影长度等，为尽可能获得精确的结果，所用仪器均专门调制以保证水平稳固，天文象限仪则仿照皮卡尔的方法设置精密望远镜。通过数次细致观测，确定两端北极高差1°1′32″，推出经线1°弧长195里6步。为简便计算，康熙将该值取整为200里。(20)依安多报告所言，步等长度单位皆应相应缩短为原长的39/40。但此一变更实际曾否进行，尚存疑问。又按1里=360步(180丈)和角度60进制换算，1′对应1200步(600丈)，1″对应20步(10丈)，亦皆为整数，极便推算。

关于这次测量，中文史料也有记载。据官方文献，四十一年康熙南巡，十月初四(11月23日)到达德州，初五至二十日(11月24日—12月8日)因皇太子患病，驻跸行宫([36]，册17，页9621—9662)。《榕村续语录》亦载，康熙“至德州，东宫病作，驻跸焉”，继而叙述其在此期间与时任直隶巡抚李光地(1642—1718)谈话，提出“明初营造尺竟是古尺”，并论述如何利用“西法”(以单摆计量炮声每秒里数)和累黍予以验证，之后谈到：

又历家云，天上一度，抵地上二百五十里。朕虽未细测，觉得有二百五十里。刻下已叫三阿哥自京中细细量来。三阿哥算法极精，如今至德州，虽少偏东，用钩股法取直量来，钉桩橛以记之，再无不准者。[56]

十月二十一日(12月9日)，康熙起程回京，对李光地说：“三阿哥已量来了，恰好天上一度，地上二百里。”李光地以为，若按周尺为当时八寸换算，“恰是二百五十里当一度也。”康熙对此表示肯定，曰：“正是。余此行大有所得。少知得算法，又考求得明尺即古尺，存古人一点迹，亦是好的。[56]”二十四日(12月12日)回銮途中，康熙又谕示随行的张玉书(1642—1711)和李光地：

用仪器测量远近，此一定之理，断无差舛。万一有舛，乃用法之差，非数之不准。以此算地理、算田亩，皆可顷刻立辨，但须细用工夫，方能准验，大抵不离三角形耳。三角形从前虽无此名，而历来算法必有所本，如勾股法亦不离三角形，是此法必自古流传，特未见于书，故不知所始也。([57]，卷5，页4—5)

康熙对使用仪器测量远近距离的准确性予以充分肯定，这显然与他早年就此学习、操作、推算的亲身经历以及当时进行的测量活动不无关系。

这次测量和康熙的相关谕示给李光地留下深刻印象。他后来在《历象本要》中论及由地理经度不同造成的“里差时刻”，指出“北极高下殊，而地有南北之纬差；时刻早晚异，而地有东西之经差”，并附记往事：

壬午冬，銮舆南巡，命皇子领西洋筹人自京城南至德州，七百余里，立表施仪，密加测望，淹历旬月，乃得星度道里之真，计地距二百里而极高差一度。旧说云二百五十里者，大疏阔矣。然所用者今工部营造尺，或古尺当今八寸，则未可知尔。臣地实扈从与闻之。[58]

对照西文材料，此处所称“皇子”即胤祉，“西洋筹人”即安多([59]，页54—55；[41]，页185)，而“立表施仪，密加测望”正是对使用仪器测量的描述。(21)约康熙五十二至五十三年间，魏廷珍(1669—1756)等奉旨将其乐律知识的学习概要写给李光地，后者见到“古尺当今营造尺八寸”的谕示，再次重提旧事：“忆前岁皇上遣官立表量地，自京师至德州，约极高移一度而地差二百里，合之古人二百五十里而差一度之说，正为古尺得今之八寸也”([60]，页17)。

对于四十一年大地每度里数的测定结果，康熙颇为自得，后来在不同场合反复提及。四十三年(1704)十月，他向大学士等谈论尺度和量制规范时指出：“天之一度，即地之二百里。但各省地里有以大尺量者，有以八寸小尺量者，画地理图稍有不合者，职此故也。[61]”五十年(1711)，借朝鲜人越境杀人案审理之机，他密令穆克登(1664—1735)勘定中朝边界，同时将此前传教士未能前往的长白山一带详加测绘，五月就此事与大学士等谈话[62]：

天上度数，俱与地之宽大吻合。以周时之尺算之，天上一度，即有地下二百五十里；以今时之尺算之，天上一度，即有地下二百里。自古以来，绘舆图者俱不准照天上之度数推算地里之远近，故差误者多。朕前特差能算善画之人，将东北一带山川地里，俱准照天上度数推算，详加绘图视之。([36]，册19，页10670—10671)(22)同日《实录》记载([31]，卷246，册6，页440)与所引《起居注》基本相同，个别字词略异。

这段谕示强调经线度数与弧长的对应关系对舆地测绘的根本性作用，亦表明经线每度里数标准在四十八至四十九年间(1709—1710)满洲测绘时确在遵行。约在此前后，康熙所撰《量天尺论》亦言及天地度数相应，再次指明“地之一度，以周尺测验，得二百五十里而无余；以今尺测验，得二百里无余”([57]，卷19，页11)。(23)关于《量天尺论》，参见文献([41]，页91—92)。冠有“御制”之名的《数理精蕴》，下编“首部”开篇规定“度量权衡”，其“里法”中便载入此一标准([63]，卷1，页5)。(24)与此相应，《数理精蕴》编入《算法纂要总纲》例题时亦将有关里数予以更正。《算法纂要总纲》第6节“三率求四率之法”有题曰“有地球二度，系五百里。今七度，该里数若干？”([64]，页117)，《数理精蕴》改题设为“设如天上二度，当地面四百里”([63]，卷3，页7)。五十五年(1716)，据全国测绘结果制作的《大清中外天下全图》，经纬线每半度交错形成网格，图说则称：“用仪器考北极高度，绘中外舆图，每方百里。自北距南二百里，则北极高一度；自南距北二百里，则北极低一度；距百里，则半度。余各有差。[65]”五十八年(1719)二月《皇舆全览图》告成，康熙命九卿大臣观看，诸臣的赞语中也有“极高差一度，为地距二百里”之辞([31]，卷283，册6，页765)。此后该标准逐渐为人所知，如曾在蒙养斋学习的算学家梅瑴成(1681—1764)不仅在自己的论著中采用新测里数，还据之改订乃祖梅文鼎(1633—1721)的旧作。(25)梅瑴成《里差论》有注“地差二百里，则天顶差一度”([66]，页21)。梅文鼎《历学疑问补·论周髀所之说必在唐虞以前》言“北极髙一度，则地面差数百十里”，下注“屡代所测微有不同，今定为二百五十里”([67]，页12)，梅瑴成改订里数为“二百”([68]，卷49，页12)。

4 康熙时代测量学知识在宫廷的传播：《测量高远仪器用法》

康熙时代宫廷内曾翻译、编纂有多种历算书籍，如《几何原本》《算法原本》《算法纂要总纲》《测量高远仪器用法》《比例规解》《八线表根》《勾股相求之法》《借根方算法》《借根方算法节要》《比例表用法》《数表用法》等著作及各类实用算表。它们最初是供康熙帝学习的讲义和参考用书，后来则成为纂修《数理精蕴》的基础。(26)关于康熙时代宫廷编撰的数学书籍，李俨1930年代初已留心考察北平图书馆、故宫图书馆等馆所藏，并认识到《数理精蕴》系据此修正而成，参见文献([69]，页158—160；[70]，页12—13；[71])。韩琦在《康熙时代传入的西方数学及其对中国数学的影响》中系统考察了这些宫廷数学著作，后又发掘里昂所藏诸书，考察《算法纂要总纲》诸本异同，揭示出宫廷数学著作编纂的复杂过程，参见文献([72]，页22—43；[11]，页147—154)。其中，《测量高远仪器用法》为测量学专论。所谓“测量高远”，即间接测量高程(含高度、深度)与远距(含长度、广度、斜距等)的直线长度，是实用几何学和测量学的基础。

4.1 《测量高远仪器用法》的内容

《测量高远仪器用法》篇首为凡例，其后内容即各种测量方法的23题(表1)，可大体分为3类。前14题使用“仪器”，其中题1—8、题13—14只需简单的比例推算，并设有比例规用法，或用“平分线”代三率法，或用“测量线”代查八线表及三率法；(27)具体算例可参考题1“有知远不知高求知高之法”([73]，页1—2)。除版本比较外，本文引注《测量高远仪器用法》，皆据中国国家图书馆藏清抄本(A02726)即文献[73]。题9—12相对复杂，需要利用三角学多次测算。题15—20及题23使用水碗、测竿等器具测量，而皆以相似直角三角形边长作比例推算。题21、题22是不借助器具估算远距的方法。(28)题23“不用仪器求高远之法”实际需要“手执一尺”([73]，页23)。

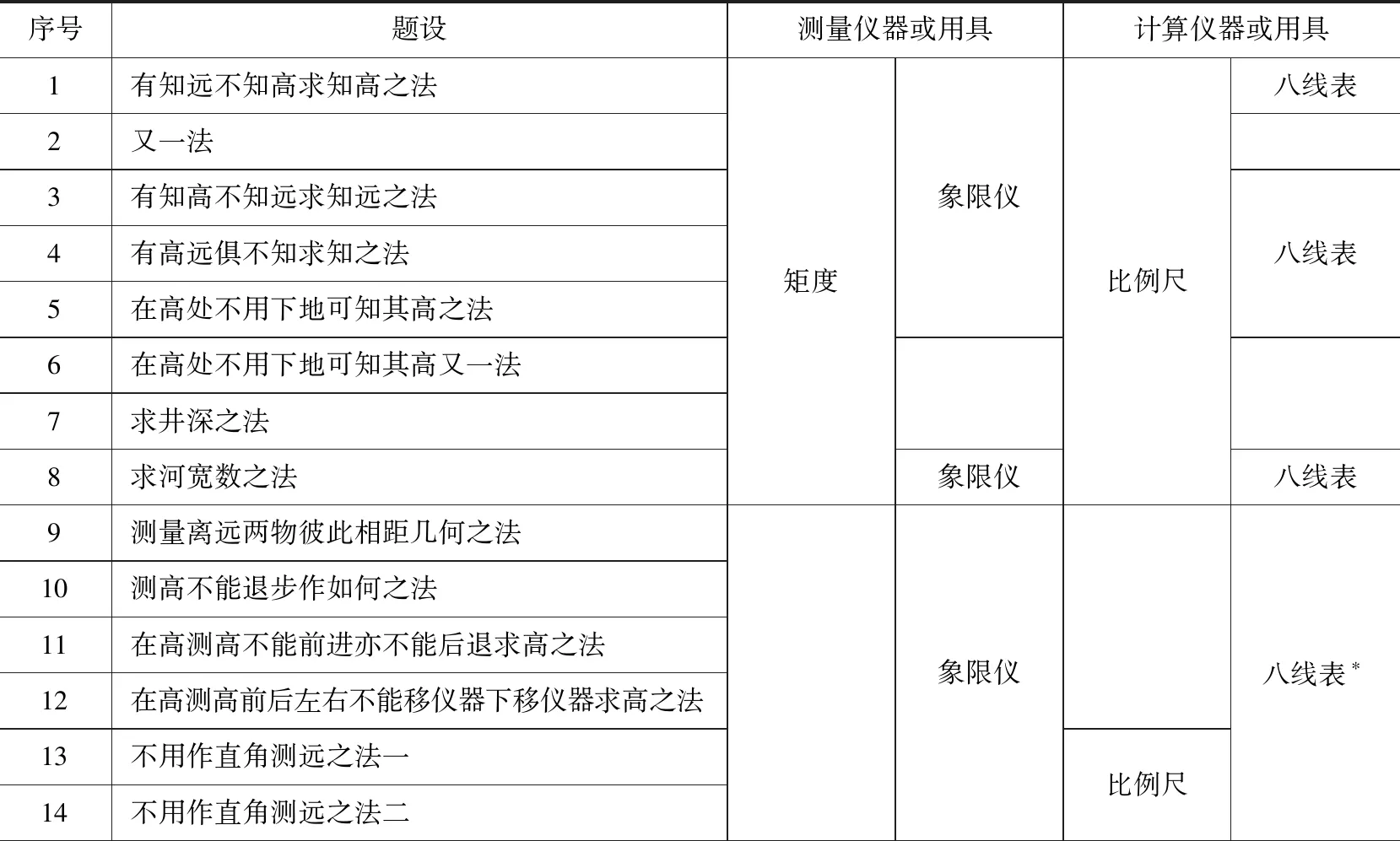
表1 《测量高远仪器用法》各题和所用仪器或用具

续表1

* 此六题实际使用八线表，只是题中未明确言及。

通观全篇，“仪器”诸题均以“有高远俱不知”“求井深”“测高不能退步”等已知情形或求解对象为名；其他题名则大多点明所用测量手段或工具，如“水平测”“用竿测高远”等等。由此表明，所谓“仪器”并非泛称，应是特定的一种。关于此仪形制，仅有凡例中的简略说明：“此书之用，俱是照仪器高线、地平线之三十分数录者。但仪器或有三十分，或有五十分，而至百分等等不同，随造仪器之便。”([73]，页1)再看其具体用法：

安仪器于所立之处，将地平直线坠定，稳住仪器勿动，将测表眼与塔尖相对，取必直一线中，察表与高线几分相交，假如与二十五分相交，则以地平线为一率，相交二十五分为二率，离远八十丈为三率，……([73]，页1)

从比例算法可以推知，“三十分”“二十五分”均是仪器之上的分度即比例长度，据此判断，所谓“地平线”“高线”当即前揭固定式矩度的直影与倒影，(29)明季《测量全义》介绍的固定式矩度形制“立边书高深，平边书远”([24]，卷3，页9)，与此略同。“测表”则指窥衡。同题另法又称“看测表与仪器周围度线几度几分相交”([73]，页1)，其值用八线表正弦入算，“几度几分”显系角度，而“周围度线”应即象限弧。总之，书中径称的“仪器”具备分度与角度测量功能，应是矩度、象限仪内外嵌套的组合仪器。值得指出的是，使用此仪的14题中，有6题以矩度和象限仪分别测量，而推算结果一致，可以互为验证，有利于初学者的理解。

相较明季传入的测量学知识，《测量高远仪器用法》在方法上有不少更新之处。如题10“测高不能退步作如何之法”(图2)：

设有如一远山，欲测其高，不能退步，亦不能前进。欲求高数若干，则先邪安仪器于丁，不动表对丙，转表对甲，察测表得几度，假如得八十度，为甲丁丙角之数。将丁与丙横线有几丈量准，假如得十丈。再移仪器，邪安于丙，将不动表对丁，转表对甲，察测表得几度，假如又得六十八度，为甲丙丁角之数。……得丙甲丁角三十二度。用三十二度之正弦为一率，……得十八丈五尺，为甲丙线数。([73]，页11—12)

前揭《测量全义》象限仪用法有平置或侧立两种方式，此处则用“斜安”以测量斜面角，(30)事实上，《测量全义》介绍的某些方法需要斜置象限仪测量或设置角度，但未予明确说明。即以所测远处高点与平地两点在斜向平面构造三角形，测量其平地边长及相邻两角，以求得一边斜远。《测量法义》曾介绍“以平镜测高”([22]，页17)即利用镜面反射的测量方法，但仅用一次，限于高远互求；该书的“水平测法”则首次引入“高远俱不知”“从两所测山之高”([73]，页18—19)(图3)等两次利用的方法。又题21测湖宽、题22测云距并不借助器具，实因所测目标相距较远而须“取圆式”([73]，页22)，即考虑地面曲率，方法新颖，亦有助于地圆学说的理解。(31)在此之前，南怀仁在《灵台仪象志》中已经介绍某些考虑地球曲率的测量问题，参见文献[74]。在编撰风格上，该书也较明季同类著作表现出更为鲜明的实用特征。如题目名称中的“在高处不用下地可知其高”“在高测高不能前进亦不能后退”“在高测高前后左右不能移仪器”等表述，显示出编者尽可能将这些方法置于实际场景以解决具体难题的考量。书中还注意指出某些方法在实际情形中的适用性，如强调“大凡用日影测法，若高远俱不知，不便于午时”并解释缘由，测湖宽则注明“此法远六七里之外者可用之，近者不便”([73]，页21—22)。

图3 用水平镜面前后两次测高图示([73]，页19)

4.2 《测量高远仪器用法》的编纂

就目前所知，《测量高远仪器用法》现有四种抄本存世(表2)。北京故宫博物院图书馆藏一部(32)影印收入《故宫珍本丛刊》，见文献[75]。；中国国家图书馆藏一部，为康熙十三子怡亲王胤祥(1686—1730)安乐堂原藏，后为孔继涵(1739—1783)收藏；又法国里昂市立图书馆藏有两部，为康熙年间来华的法国耶稣会士巴多明(Dominique Parrenin，1665—1741)寄回([76]；[69]，页158；[11]，页148—150)。(33)中国科学院自然科学史所另藏一部，系李俨依国图藏本影抄。经查对，四种抄本分属于两个版本系统，即(甲)国图藏本与里昂藏本一(Ms.82- 90 D)；(乙)故宫藏本与里昂藏本二(Ms.75- 80 D)。诸抄本均不分卷，共23叶，半叶13行，行15字。其文本内容亦大体相同，唯甲类抄本叶22“不用仪器测远法”(图4)和“测远望去有如与地平相等之云法”各多一段简短附语：

此地半径，用九万里变丈尺求径，半之即地半径也。径折半毕，以一百八十丈乘之。

此地半径，用九万里求径，折半即地半径也。([73]，页22)

图4 《测量高远仪器用法》国图藏本(左)和故宫藏本(右)“不用仪器测远法”([73]，页22；[75]，页479)

所谓“九万里”即地球周长，合1度250里。(34)甲类抄本地球半径“二五七七六〇〇”(步)和“一四三二四里”([73]，页22)即据引文算法估算，乙类抄本虽删去地球周长“九万里”两段，但地球半径值([75]，页479)并未相应改订。又甲类两本皆与《比例规解》《八线表根》同在一册；乙类两本皆与《比例规解》同在一册，其后皆有《地平线离地球(圆)面表》(故宫藏本在同册，里昂藏本二在后册)，该表系依照“二百里为一度，三里零六十丈为一分，十丈为一秒”编制。(35)引文据里昂所藏《地平线离地球圆面表》([77]，书衣题签小注)。书内所称“远数”即度数对应的经线弧长，一秒、一分、一度“远数”([77]，页1，2，10)与此规定数值吻合。故宫所藏《地平线离地球面表》影印本文献[78]未见书衣，四十一秒至一分四十一秒整叶阙。图示方面，甲类抄本相对简略，乙类抄本更为精细，特别是“用日影测高远法”之图，甲类抄本全无楼宇等实景，仅以几何虚线表示其高(图5)。综合考量，甲类抄本当系初稿，其成书应在前所述康熙四十一年修正地球经线每度里数以前。乙类抄本定稿较晚，当是四十一年以后略加删订，并附《地平线离地球(圆)面表》。

表2 《测量高远仪器用法》现藏诸本及异同

图5 《测量高远仪器用法》国图藏本(左)与故宫藏本(右)日影测法图示([73]，页21；[75]，页479)

《测量高远仪器用法》不著撰人，最有可能是安多编纂。他在编译《算法纂要总纲》《借根方算法》《借根方算法节要》以外，还曾教授比例规用法并编写专论(de usu circini proportionis)([13]，页141)，编制中文的正弦、余弦和正切数表([6]，页57)，故而《比例规解》《八线表根》也可推定为其著作。鉴于安多曾主持大地经线1度弧长的实测，《测量高远仪器用法》的测量方法阐述详明，又多用比例规、八线表计算，且与《比例规解》《八线表根》先后合订于同册，应当也是安多所作。(36)韩琦之前已有此推断，参见文献[11]，页150脚注①。又据前揭《地平线离地球(圆)面表》与《测量高远仪器用法》的关系，该表亦当是安多制作。

此外，《测量高远仪器用法》所述测量学知识与安多自著《数学纲要》多有相似。《数学纲要》第三章《论实用几何》(De Geometria Practica)共六节，第一节“论直线三角形的解法”(De resolutione triangulorum rectilineorum)、第五节“论面的测算”(De superficierum dimensione)、第六节“论体的测算”(De dimensione solidorum)分别编译为《算法纂要总纲》之“算三角形总法”“算各面积”“算体总法”([11]，页152)，而其余三节皆与测量有关：第二节“论几何(测量)仪器”(De Instrumentis Geometricis)、第三节“论度量”(Mensuris)([79]，页145—160)是预备知识，第四节“论线的测算”(De dimensione linearum)([79]，页161—181)即讨论高远测量，除第二、第四款为一些塔和山的高度外，就是阐述具体方法的19道命题。《测量高远仪器用法》与《数学纲要》的测量方法可以建立某些对应关系。如前书“测井深之法”即与后书“测量井的深度”(Putei profunditatem metiri)所用仪器、方法相同([73]，页8；[79]，页181)；前书“用日影测高远法”中的以远测高之法，亦同于后书“用影子测量”(metiri per umbram)([73]，页21；[79]，页162)。又，前书“有高远俱不知求知之法”的矩度与象限仪测法，可分别与后书“用度高标尺测量不能到达的塔的高度”(altitudinem turris inaccessae metiri scalaltimetr)和“当塔不能到达时测量”(meriti， quando turris est inaccessa)的内容对应([73]，页4—5；[79]，页164—165，166—167)。

还有例证显示出两书之间的紧密关联。其一是特殊的测量方法。《测量高远仪器用法》测云距之法，要求“有云远望之如与地平相等”([73]，页22)(图6)，如此便可利用视线与地面相切而构成的直角三角形求解；而《地平线离地球(圆)面表》亦据此计算“离数”即相应度数的地表弧线与地平切线之间的离差。《数学纲要》“论线的测算”命题14“测量山的绝对高度”(Montis altitudinem absolutam metiri)测算原理完全相同，即立于地平平望远处山顶，再利用视线与地径相切测算山峰海拔高度([79]，页175)(图7)。其二是特殊的测量仪器。前揭《数学纲要》第二节“论几何仪器”一节，分为测角仪器(De instrumentis ad angulos metiendos)与测线仪器(Instrumenta ad lineas mentiendas)两款，前者包含天文象限仪(quadrans astronomicus)，后者则有矩度(度高标尺，scala altimetra)和比例规(circinus proportionalium)两种([79]，页145—146，150—152)。其矩度图示(图8)内含象限弧，与《测量高远仪器用法》的“仪器”即矩度和象限仪的组合样式相应；(37)安多曾受命制作一具名为pyxis quadrata的组合仪器，其外部有天文象限仪，内部画有测量(几何)仪器([13]，页141)，或即《测量高远仪器用法》所用。将比例规视为测量仪器的归类方式，亦与《测量高远仪器用法》多使用比例规计算的特点一致。

图6 《测量高远仪器用法》测云距图示([73]，页22b)

图7 《数学纲要》所示测山高([79]，Lam.14)

图8 《数学纲要》所示矩度样式([79]，Lam.8)

以上考察表明，《数学纲要》“论线的测算”一节应是《测量高远仪器用法》的编纂基础。两书讨论的测量学知识多有相关，文本内容、结构、体例则不尽相同。(38)《测量高远仪器用法》总体上以测量仪器与用具为中心，而《数学纲要》则以测量对象为中心，将高度测量与长度、广度、深度的测量分作不同类别；前者各题均有详细步骤并设具体数值测算，而后者各命题一般仅阐述简明方法，并不举例演算(仅Prop.VIII附有一个演算实例)。鉴于安多本人的数学素养，他完全有能力在《数学纲要》的基础上增补若干测量方法，并以仪器用法为中心，编纂成一部实用、易解的测量学讲义。

5 余论

作为欧洲实用几何学的重要内容，测量学知识在康熙时代的科学传播中扮演了重要角色。自西学研习之初，康熙帝就对测量学及其仪器操作情有独钟，不仅在耶稣会士的指授下亲自推算和实践，还因军事、河工等治国之需，屡屡派员测地绘图。特别是康熙四十一年自霸州至交河的大地测量，由皇帝策划、耶稣会士安多主持、皇三子胤祉组织实施，在此前法国科学院同类工作的基础上，沿地表经线丈量约1度的弧线长度，由此确立每度里数，为全国范围的舆地测绘奠定了标准。

康熙四十一年大地每度里数标准确立之际，康熙帝在向张玉书、李光地谈论“用仪器测量远近”的谕示中，还提出三角法在中国古已有之的论调。次年(1703)七月，他就此加以阐发，撰成《御制三角形推算法论》，正式提出“西学中源”说，并不断向臣属论及([3]，页2—4)。(39)另值得指出的是，四十一年康熙南巡谈论测量话题的同时，李光地亦曾以梅文鼎《历学疑问》进呈御览，次年春蒙批点发还，此后梅氏《三角法举要》《弧三角举要》《堑堵测量》《环中黍尺》等此前多已成稿三角学著作集中在保定校订刊印，很可能与康熙关于三角的论说有关。四十一年的大地测量活动可说是促使康熙迈向“西学中源”的关键因素之一，引发了深远的历史影响。

大地每度里数测定以后，康熙帝仍对测量知识保持着浓厚兴趣。四十八年(1709)五月，正值传教士在满洲测绘之际，他召见算学家陈厚耀(1648—1722)，在询问所学之后：

午刻，内侍李玉传旨问：汝测量是何法？臣跪对云：测量之法，由近可以测远，由卑可以测高，由浅可以测深。又问：能用仪器否？臣对云：臣家无仪器，只用丈尺亦能测量，与仪器同是一理。仪器以圆测方，须用八线表；丈尺以方测方，直用三率法。([80]，页30；[81]，页28)(40)关于所引两篇文献及其解读，参见文献[82—83]。

这段君臣对答既体现出陈厚耀对测量方法及其原理的良好掌握和理解(41)陈厚耀曾作《测量法义》一篇，概论高远测量的基本原理与方法。，也反映出康熙对这类知识特别是用仪器测量的长期关注。五十年(1711)二月，康熙巡阅通州河堤，又偕多位皇子和满汉大臣测量河岸距离并示范仪器用法：

于是取仪器插地上，令将豹尾鎗纵横竖立，上亲从仪器者定方向，遣雍亲王、恒亲王、尚书黑硕色、侍郎揆叙分头钉桩，以记丈量之处。又于尽头处立黄伞，以为标准。上席地而坐，命皇太子测报仪器度数，回取纸裱方形仪盘，置于膝上，以尺度量，用针画记，硃笔点之，算毕，令从尽头处丈量至所插仪器处，其丈尺与所算之数吻合，随侍臣工无不称奇。([36]，册19，页10506—10507)(42)同日《实录》记载([31]，卷245，册6，页431)与所引《起居注》略同，但省去部分细节。

五十二年(1713)万寿庆典之际，王鸿绪(1645—1723)呈献的礼物中有“西洋察量远近仪器一个”[84]，迎合了康熙对欧洲测量仪器的喜好。(43)关于此次庆典与康熙朝后期宫廷历算特别是蒙养斋算学馆成立的关系，参见Han Qi, “1713: A Year of Significance,” lecture, REHSEIS, CNRS, Paris, 9 January,2007, https://www.academia.edu/8278554.对康熙帝而言，终其一生，钟情于测量，反映出科技知识在皇权统治中的重要作用。

《测量高远仪器用法》是康熙时代宫廷编纂的测量学专著，该书以一种矩度与象限仪合一、分度与角度兼测的“仪器”为中心，系统解说其在各类实际场景中的用法，而旁及其他测量方法。该书的内容相较明季的介绍多有更新，充分体现了当时宫廷数学教育注重理解、偏向实用的特征。多方证据表明，该书应为安多参考其西文著作《数学纲要》的测量学内容并补充相关材料编纂而成，在康熙四十一年大地每度里数测定后略加修订，和《比例规解》《八线表根》《地平线离地球(圆)面表》等著作一道，为后来全国大地测量提供了必备的知识基础。“测量高远仪器”也在舆地测绘中广泛施用，更以康熙“御制方矩象限仪”之名编入《皇朝礼器图说》[85]，成为国家仪制的组成部分。康熙五十二年蒙养斋开馆修书后，《测量高远仪器用法》亦有不少内容融入《数理精蕴》之中，这些知识的后续编纂与完善，尚值得进一步探讨。

附录

关于1702年12月在中国直隶进行的地球一度的测量(44)吴旻据文献[5](tome 46，页160—178)译出。

中国鞑靼的皇帝康熙曾经命人绘制了整个中国以及他辖下的鞑靼地区的地图，是中国人和鞑靼人用墨线绘制的。地图有不少谬误，皇帝想纠正过来，并且还想在图上增加原本没有的经纬度。之前皇帝曾经和南怀仁神父谈到过这个计划，后者建议他从中国地区入手。然而不久之后南怀仁神父就去世了，而且与厄鲁特部以及噶尔丹非常艰险的战争也爆发了。因此皇帝不再考虑实施这一计划，在接下来的几年之内，他只是埋头于学习数学。

噶尔丹死去、战争胜利之后，皇帝又重新考虑这个计划。他首先派遣了我会的两名神父去往西鞑靼，这一地区在其统治之下未遭战火侵袭。这一漫长艰苦的远征尽管曾使得我们面临生命危险，但我们甘之若贻。这是一个极好的机会让我们走过这片人口稠密的辽阔土地，似乎从未有过福音的宣讲。1698年5月24日，我们出发，三位管理西鞑靼藩王的理藩院高官同行。六天行程之后，我们跨越了中国与鞑靼的分界线长城。再走了相同天数，这期间我们遇到了一些村庄以及这里那里零星的耕地。然而再往前走，我们就只看到鞑靼人的帐幕以及数量可观的牛羊。我们继续向北偏东方向前进，6月30日，我们在一个名为贝尔(Puyr)的大湖前扎营。在这个湖与另一个名为呼伦(Colon)的大湖之间，各部藩王进行七天的会盟。这里的北极星高度是48°3′。我们继续向西行进，沿着游满鱼虾的克鲁伦(Kerlon)河，它穿过牧草丰饶的平原。走过900里(stade chinois)，沿途一直在测算，每一里是360几何步(pas geometrique)，我们扎起帐篷，而此地正是1696年皇帝扎营驻跸之处，也正是从这里噶尔丹溃逃出去。从这里开始，我们相继遇到了与此事相关的地方。我们最终告别了克鲁伦河，在8月3日抵达了土拉(Tula)河。我们扎营之处正是在同一年噶尔丹被皇帝的两支军队之一彻底击败的激战之处。当时整个地区荒无人烟。之前在此居住的鞑靼人不是被噶尔丹剿灭就是押往别处。土拉河，水质清澈、鱼虾丰满，它在树木青葱的群山环绕下令人心旷神怡的谷地流淌约900里之后流入鄂尔浑(Urgon)河的怀抱。它们的汇合点离厄鲁特城市什尔噶(Siriga)约300里。这个汇合点也是第二次藩王会盟的地点，厄鲁特部也过来参加。我们在8月13日到达此地，并测得北极星高度为49°3′。几天之后，我的同伴张诚神父，一向身强体健，但这次不适已有几天，突然病重垂危。然而由于天主特殊的恩典，他出乎意料地坚持了下来。他由车子载回北京，最终性命无虞。(译者按：中间写他带了一本天主教的书，试图传教等等，略)我们回程往中国地区走了另外一条路，并于10月2日到达，那是一个名为呼和浩特(Kokohoton)的小城西边，北极星高度40°54′。从这里开始土地有了耕作的痕迹，我们可以看到一些村庄。10月10日，我们从张家口入关至长城以南，再走了5天，我们于10月15日抵达北京。

皇帝不在宫中，正由东鞑靼地区回京的路上。12月8日我去迎接他。看到西鞑靼地区的图样之后，皇帝表示非常满意，并且计划来年去往东鞑靼地区的行程。他对我说：“朕要你从朝鲜边境一直走到东海，然后沿着海岸走到日本的北方边境，那里与东鞑靼仅隔一道很窄的海峡。”这并未让我感到不快，我说明一下：我可以由此对这些地区有更好的认识，也许有一天会对圣教有用。皇帝定下了我的出发日期并且发了旨意。但是之后发生了一些事件，服从肯定比牺牲要好。这一旅程被推迟了，之后就被取消了。这一年正是黄河泛滥，皇帝让人画下了堤坝的高度，以及黄河入海的路线，亲自研究治理的方法并且掌控整个事件。

而就在上文说到的那一天(译者按：注释里说是12月8日)，皇帝满怀兴趣长时间看着西鞑靼地图。他发现纬度的距离与之前测量的不符，之前测量过的是从长城直至土拉河由南至北的开放平原。事实上，根据汤若望神父刊印的数学著作，一度相当于250里；而根据我们沿途的测算，一度则多数时候等于200里。皇帝询问产生差别的原因。我回答说一般中国的里都小于皇帝使用的标准里，比例大约是4至5。而我自己经过鞑靼平原的时候，比较过北极星高度与官府测定的道路，一度最多也就等于皇家标准的200里。皇帝对这个理由表示满意。然而，他也到看到良好观测带来的巨大益处，也懂得了为了得到好的观测效果，与一度相关的标准里数应该是确定不变的。为此，在几年以后，即去年的4月25日，他下令测量准确的一度的距离长度，并且为了完成测量，选定了一块平整的地块，但却把测量的时间定在了秋末，是为了既不因测量影响了秋收使得百姓受损，也不因秋收影响了测量。

10月20日，按照惯例在鞑靼狩猎避暑三个月的皇帝回京，用于测量的仪器被呈至他面前。11月4日，他任命他的第三个儿子，人称皇三子来跟进此事并合作。皇帝曾经在几年间将自己所学亲自传授给他。王爷得益良多，并且成为了一位敏锐的观测者与迅捷准确的计算者。当月14日，皇帝出发前往南京，巡视河工及遭遇黄河水患的地区。之后不久王爷就派出自己府里以及钦天监熟悉北京周边的人，寻找合适测量的平原。在200里方圆当中，都是平整的田地，但是长满林木。最后从霸州至交河，他们找到一块空地，平得像海面，一点起伏都没有，大约有200里。当图样拿回来的时候，我们商议了一下，把出发日期定在11月28日。

出发前一天，仪器都被运到王府。王爷的战俘将会负责第一天的搬运，之后会有沿途各府县的挑夫接替运输。为了保证测量的顺利进行，皇帝命令钦天监的满洲监正沿途负责。他带了7个手下监督运送的挑夫。同一道圣旨里，还下令6位其他部院的官员一同随行。他们将随时听命于我们。还有一位宫中的满洲官员赫世亨，他负责找到及征用一切必需品。他雇用了木匠与画工。上文所说的28日，我们离开北京向南行进。王爷第二天乘轿前来，带了大批随从。我们在第三日会合，在听过第二批派出确定情况的人员汇报之后，我们确定在霸州原定地点进行测量。

我们于12月1日抵达霸州，次日早晨，我们在县城东门靠近城门的地方，选择了一座田野当中很显眼的用石头砌成的古建筑作为标志，然后我们从那里开始测量子午线。下面是我们测量的方法：我们拿着一根很直的一里长，即360步长的铁线。为了避免它偏离子午线，我们每隔120步打一个桩。这些桩都搁在三脚铁上，带有铰链，以便使得它们取得并保持垂直状态。为了画出子午线，我们在每一里的前面都配置了最好的调整好的仪器，包括两架望远镜和一个长针罗盘，以便我们在旷野之中利用经过子午线的北极星这一绝佳方法来确定磁偏角。磁偏角度数是2°1/2，与北京一样，在整个测量过程中都没有变过。

我们用180根杆子测量第一里，或是360中国步，与古罗马步相比就是16至15。然后再测下一里，直到所有的，遵循的是以下方法：在最远处的那根杆下，我们放一个十分精密的仪器，从一边向另一个方向瞄准，可以看到所有的桩都在一直线上。然后这直线延长至下一里，三个桩间隔120步。这些桩也放置得与前面的一样在一直线上。由于这整片地区十分平整，因此仪器的横向的两端也都指向各桩。我们用来测量的铁线，就架在桩上，并且有大量的测量员看着，以防它跑偏。王爷以及随从在场，极大提高了测量的速度。长时间习惯于摆弄这些仪器，这是一位有着敏捷思维且有远见的年轻人。他用仪器进行观测，他下达的命令，他在各处有效地帮忙，都表明他坚决而带着极大热情地主导这件事。邻近府县的官员都来了，还有大批民众过来帮忙。我们还看到大批木匠待命，随时准备砍伐影响我们测量或是挡住视线的树木。在我的请求下，人们留下了大部分的果树。我们也放过了一些村庄。在整个子午线经过的区域，我们仅仅遇到了三个村庄，而且都是极小的，在这个人口稠密的国家，还是挺让人吃惊的。其中的两个，子午线，即用来测量的铁线两次都经过了非常罕见低矮的房舍，屋顶是平的，可以在上面行走，并且很方便地安置仪器及桩子。这是测量经过第74里的事情。但是到了5里之外的第三个庄子，我们转了90度，向东一里，然后我们继续测量。最后，到第97里时，我们遇到了一个大湖，但是冰面尚未冻实。这一障碍使得我们不得不转回西面一里，回到我们最初测量的子午线延长线上。

但是，为了不把我们的时间都花在数学测量上，也可做为一个很好的目的。圣沙勿略日(12月3日，原注)由于恶劣天气的阻拦，我们停留在一个叫“苑家口”的大镇上。(……见了教徒做弥撒告解……)我们甚至和教友一起享用了王爷给我送来的宴席。王爷在家宴请了所有随同的官员，但是为了避免我在大雪里奔波，他就把给我的一份送了过来。(……各种传教事，带书去宣教……)

我们来到最平整的地段测量，到199里的时候，我们又遇到一条又宽又深的河，名叫“漳河”，我们就将之作为这次子午线测量的南端。我们在河边架起来一个30步的圭表，压在我们之前刻在另一块水平梁上的子午线上面。这两根水平梁，与其他横断部分一起，组成一个大约一里见方的框，这是在北京就做好的。如指针形状竖立起来部分的顶端有一块大的薄铁片，用支撑物和挂钩牢牢固定起来。在方框之内靠近水平梁的地方，有一块扎了眼的铁板，洞眼的直径约半指宽，那里连接着一个由细青铜线挂着的重2法斤(livre)的青铜球。方框的四周用柱子支撑起来，非常稳定，完全不会在风中动摇。而水平梁，平放在子午线的方向，有两根撑杆支持，并且有铰链系统以确保它稳固及与地面平行。为了维持平衡状态，人们挖了两个槽盛放水银，其容量约为120法斤。为了更好地地辨识从圭表顶部的小孔透过的阳光，王爷在他的帐篷前面支起了一块很大白色布幕，并且在上面留好了太阳光线通过的必要开口。尽管冬日的坏天气没有让这些精心的安排与准备完全成为幻影，但是结果多少还是不那么可靠。实际上，那天是12月17日，太阳达不到30度的高度。折射光线很亮，太阳光线却很弱，加之有一小股风总在使得吊挂轻轻震荡，尽管它根本没有暴露在风中。尽管做了很全面的准备，但是天体的中心经过的时候，太阳光线只是模糊地投射在子午线上。因此，尽管眼力很好的王爷声称并且确定清楚明白地看到了太阳光线经过了子午线，但是因为我并未清楚确实地看到，对于重复做了两次的这一观测，我留有疑义。

我决定应该更加确定北极星的高度。我用了一个很大的铁与铜精心制作并刻好刻度的象限仪，在北极星经过子午线时测量它的高度。在河边一个挡风的大帐篷里，我连着在三个晴朗的夜晚观测了北极星。

在子午线圈中的北极星高度是地平线上40°21′。

当我们回到我们测量距离最北端，也就是我们测量的起点之时，我们又往北测量了一里，这样测量的两端距离就达到200里，正如皇帝之前命令的那样。在那里，我们也像在南端一样架起一个圭表，遭遇了同样的失败，主要归咎于平整田野中的坏天气。尽管错谬实际上少而又少，但我还是怀疑这一测量。于是我仍然使用上文中提到的天文象限仪，确定北极星通过子午线的高度。经过两晚的观测，我确定其高度为地平线上41°22′30″。

这个象限仪不仅有孔，还有一架精密的望远镜，可以很方便很好地看到北极星。它可以读到至少10″的弧度。由于沿途府县官员的高度警惕，它被装在合适的盒子里由挑夫挑着，一路上没有任何损坏。因此对于在线的两端所作的两次及三次北极星观测，我们相信足够细致与准确，因为我们是非常小心地进行的，并且它们的结果也互相吻合。我们是按照下列方法解决一度经线长度的：

北端北极星高度 41°22′30″

南端北极星高度 40°21′00″

差 1°1′30″

南端折射超出北端折射的部分 2″

实际高度差 1°1′32″

因此，我们就得到1°1′32″对应200里即72000步，由于1°约为70206步，也就是说1°为195里零6步。

值得注意的是，我们用同一个象限仪在南北两端测得的正午太阳高度，并将结果两相比较，得出的一度长度也基本相同，有时稍长，有时稍短，但是差异极小。而在南北两端用圭表所作的观测，可靠度稍逊，确实得出的结果要稍长。这至少说明，几次对于北极星经过子午线的仔细测量，其结果对于一度长度的估算产生的误差极小。它们是12月15、16、17日在南端以及21、22日在北端所作观测，当时的天气平静晴好。

用于测量的中国步的基准器是刻在大铁尺上的，上面刻有五步。现在它藏于宫中。正如我在前面讲过的，中国步与依据Villalpando(著作)估算出的古罗马步之比为16比15。因此可以推出一度之中有74886罗马步。已知这一尺度，就很容易推及到所有各个国家，只要知道各种度量衡之间的关系。

但是皇帝希望一度回到200里的长度，因为这个数字方便计算。因此我们之前用来测量的中国步的尺寸必须被缩短，其比例为40比39。按照新的步数，一度就有200里或是72000几何步；其中一秒为20步，一分为1200步。由此进行的计算非常简便，使用数表也更加简单快捷，不论是地平线与地圆线的间距，或是正割线超出半径的部分。

以上就是我认为应该简单写出的有关皇帝命令下进行的大地测量。希望读者不会对此感到吃惊，我们这些远离欧洲、为了在远东异教徒中传播天主福音的人，却有时进行这些与传教无关的活动。我们在这个宫廷里是为基督服务的囚徒，我们所有人所做的所有事，无论大小，从国家大事到个人举止，都是为了耶稣基督。在中国，没有官府的支持，传播圣教根本没有可能也不会取得成果。中国人是世界上最骄傲的民族之一。必须让他们认识到不是所有从外族来的都是纯粹蛮夷。必须炫耀人文科学，用惊人事例呈现在人们眼前，为福音传播者立威，赢得这些习惯于蔑视外族的人，他们就如同欧洲人看不起野蛮美洲人一般。这就是为何我们有时会在这里放弃传教事业的缘故。这是为了支持在中国刚刚建立起来的教会，并且在暴风雨中庇护它。这是为了让它快速稳定地发展，借助于皇帝和权贵不可想象的支持和仁慈。从前使徒为了赢得罗马行政官与百人队长的支持，自称为罗马公民，并未自甘为奴牺牲圣教；而我们，为了不在这个国家被视为不开化的、必须接受中国人教导的蛮夷，必须在中国人面前公开展示科学实证，展示他们可以从我们这里学到很多东西，包括最重要的东西，而圣教也不因来自异域而被视为蛮夷。特别要求得天主的垂怜，让圣教的真理战胜这个如此博学民族的智慧，坚定它的信念，让它克服感官的愉悦，并决定投入圣教的怀抱。

北京，1703年9月8日。安多