基于RFT和AMF融合聚焦的雷达弱小目标检测
2019-02-13商哲然易天柱卢大威
梁 璞,陈 兴,刘 让,商哲然,易天柱, 卢大威
(国防科技大学 电子科学学院,长沙 410073)
0 引 言
无人机、空飘气球等低小慢目标的不断增加,使现有雷达对目标的检测难度越来越大[1],对防空预警构成严重威胁。这些类型的目标对雷达发射电磁波的后向散射较弱,导致雷达获取的信噪比大大降低,雷达的探测和检测性能也随之大幅下降。从信号处理的角度出发,研究低信噪比下的目标检测方法具有重要的价值。本课题要点主要是,在检测阶段,需要采用相干积累技术增大接收信号的能量以提高检测性能,难点在于如何实现长时间信号能量的积累。
雷达弱小目标长时间相参积累问题主要考虑目标是否跨距离单元和跨多普勒单元。由于场景[1]中杂波的存在,相参积累前需要进行杂波抑制。传统的杂波抑制方法是动目标指示(Moving Target Indication, MTI)滤波器,其阶数越高对零频附近杂波抑制越好,且不会影响周围频率信号。根据对测试数据的处理与分析,本文采用57阶的FIR滤波器实现MTI。对杂波抑制后的数据进行相参积累,考虑到目标存在跨距离单元,学者们提出了一些新的检测方法来解决目标回波跨距离单元走动问题,实现目标能量的有效积累,典型方法有Keystone变换法[2]、相邻交叉相关函数(Adjacent Cross Correlated Function, ACCF)[3-4]、Radon-Fourier Transform(RFT)法[5-7]等。Keystone法使用sinc插值计算,计算量较大,ACCF对单目标效果较好,处理多目标时会出现交叉项,影响聚焦。RFT法有机地将运动目标检测(Moved Target Detection, MTD)处理和Radon变换统一起来,直接沿目标初始距离和速度确定的直线轨迹对目标回波能量进行相参积累,取得了较好的聚焦效果,但标准RFT存在运算量大、实时性差、量化损失大的缺点。针对上述不足,文献[8-9]提出了Chirp-Z 变换加速的RFT(Chirp-Z Transform, CZT-RFT)算法。该算法的基本思想是将RFT算法在频域利用CZT变换实现,从而显著提高了算法的运算速度和能量聚焦效果。进一步,考虑到小目标信噪比较低,需要在MTI的基础上对数据做进一步的杂波抑制和聚焦,常用的方法有广义似然比检测(Generalized Likelihood Ratio Test, GLRT)[10]和自适应匹配滤波器(Adaptive Matched Filter, AMF)[11],其中,AMF的运算量要比GLRT的运算量小。RFT算法对大目标的聚焦效果更好,而AMF算法对小目标的聚焦效果更好,将两者聚焦结果进行单元选大,可以将两者的优势结合,得到RFT和AMF的融合聚焦结果,将聚焦结果送入单元平均恒虚警检测器(Cell-Averaging Constant False Alarm Rate, CA-CFAR)中,得到最终的检测结果送入后续的数据处理。
1 问题模型
1.1 信号模型
假设目标为点目标,则目标相对于雷达径向变化模型[12]为
(1)
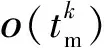
根据速度和加速度的取值情况,一般将运动模型简化为四种情形:① 低速匀速直线运动模型。该模型主要针对常规空中飞行器,认为目标具有一定的运动速度,但在积累周期内假定目标在同一个距离单元内,忽略目标的机动性。② 高速匀速直线运动模型。该模型主要针对高速运动飞行器,假设目标具有高的运动速度,忽略目标的机动性,目标在积累周期内出现跨距离单元走动现象,但距离维的轨迹可以采用直线描述。③ 高速匀加速直线运动模型。该模型主要针对高速高机动飞行器目标,在高速匀速直线运动模型的基础上,利用加速度来描述目标高机动性以及跨距离单元、跨多普勒单元现象,而且加速度还会使目标在距离维上出现运动轨迹弯曲现象。④ 高阶运动模型。高阶运动以及转动等更为复杂的运动需要更多的参数来描述目标的运动情况,相应的长时间积累方法也就变得更加复杂。
在以上运动模型中,传统的脉冲积累一般基于模型①设计,高速高机动目标长时间积累方法则基于模型②和③设计,而模型④较为复杂,根据应用不作考虑。
假设雷达发射的为线性调频信号:
(2)
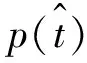
(3)
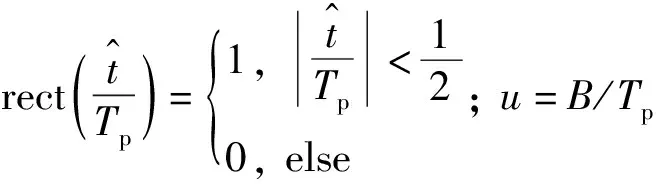
(4)
当a=0时,将式(1)代入式(4)得
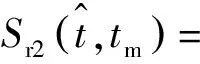
(5)
式(5)由三项组成:第一项为回波包络;第二项为载频项,表示目标初始位置;第三项为由目标径向运动产生的多普勒项。经过脉冲压缩后的回波信号为
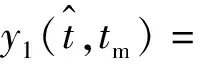
(6)
根据驻定相位原理,其频域形式为

(7)
当目标径向加速度a≠0时,目标存在二次相位,将式(1)代入式(4)得
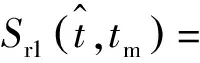
(8)
经过脉冲压缩后的回波信号为
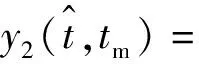
(9)
由式(9)可知,由于出现距离走动的二次时间项,脉压后结果也不再只是没有加速度情况下的一条斜线,而是呈一定弯曲的曲线。
频域形式为
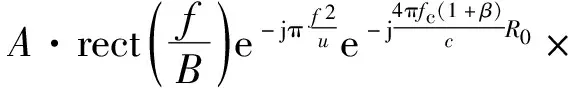
(10)
其中:β=f/fc。式(10)由四项组成:第一指数项为基带信号调频率项;第二指数项为目标位置;第三指数项为目标径向速度引起的多普勒项;第四指数项为加速度引起的调频项。
1.2 跨距离单元走动
由式(6)和式(9)可以看出,高速高机动运动目标回波随着慢时间tm变化,即在积累时间内,经过脉压后目标回波峰值不再位于同一个距离单元内,会出现距离单元走动的现象。若距离单元的大小为c/(2B),相参积累周期TCIT=MTr,则目标的跨距离走动情况如下:
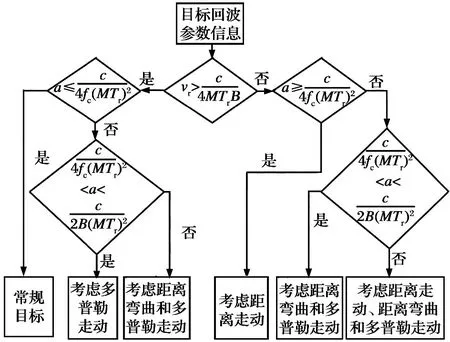
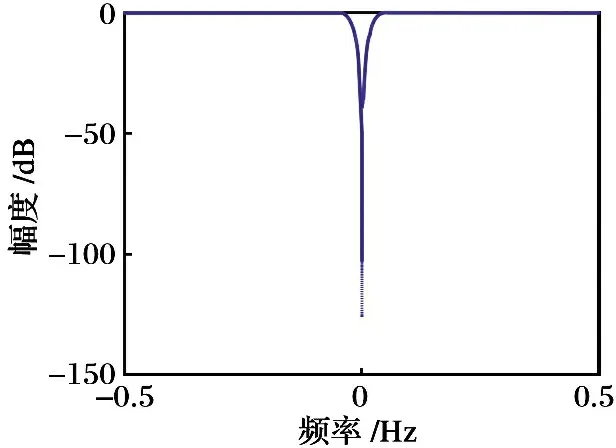
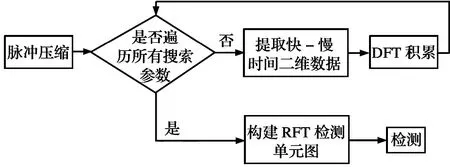
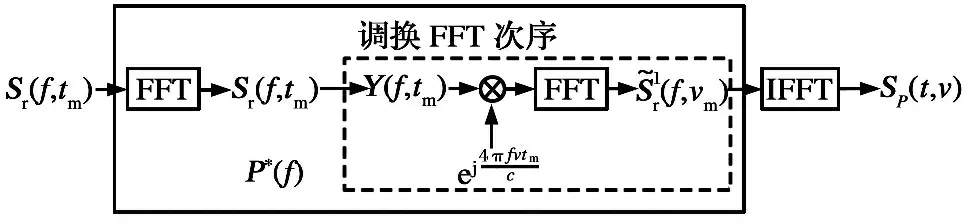
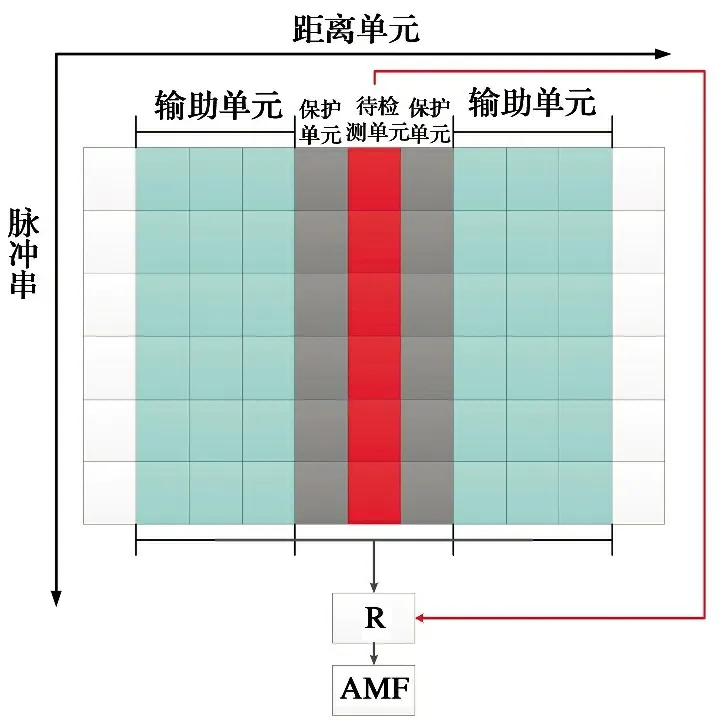
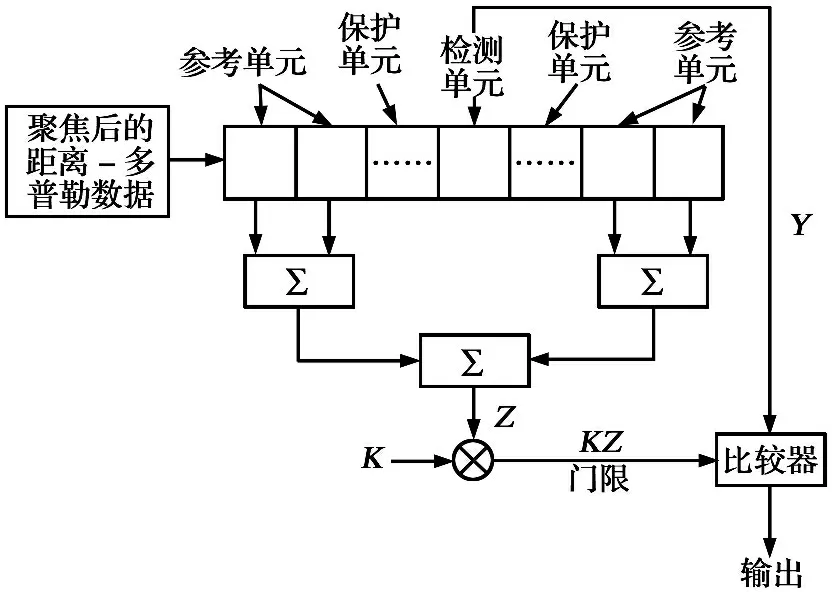
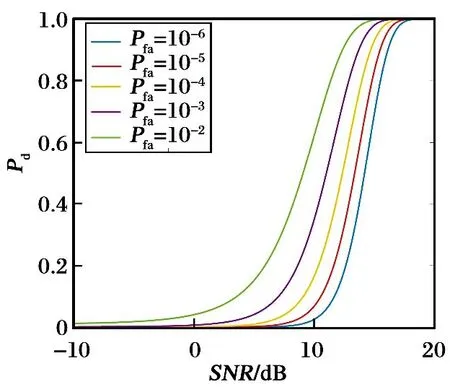
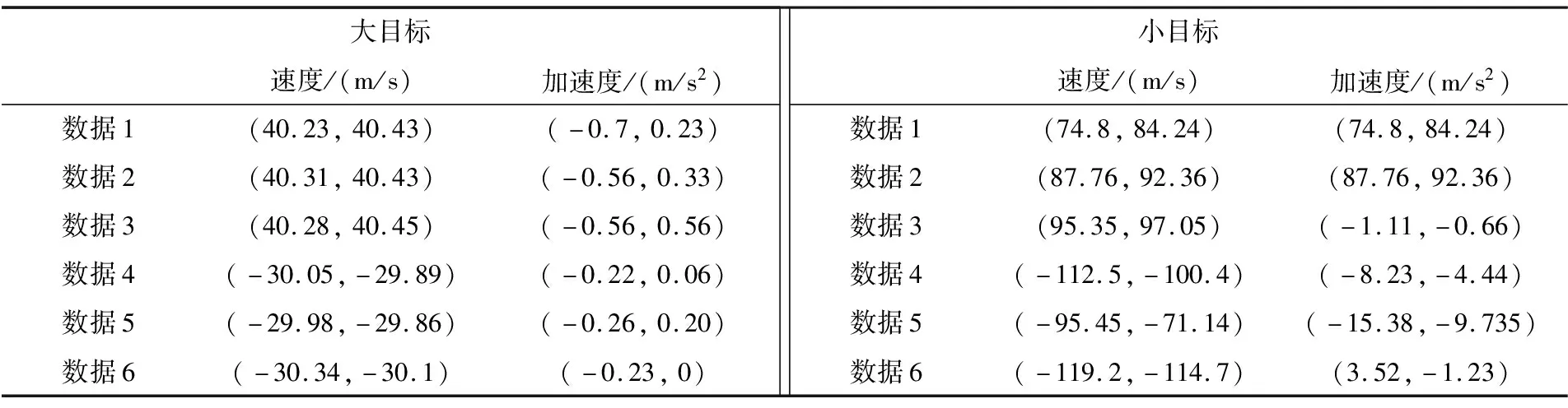
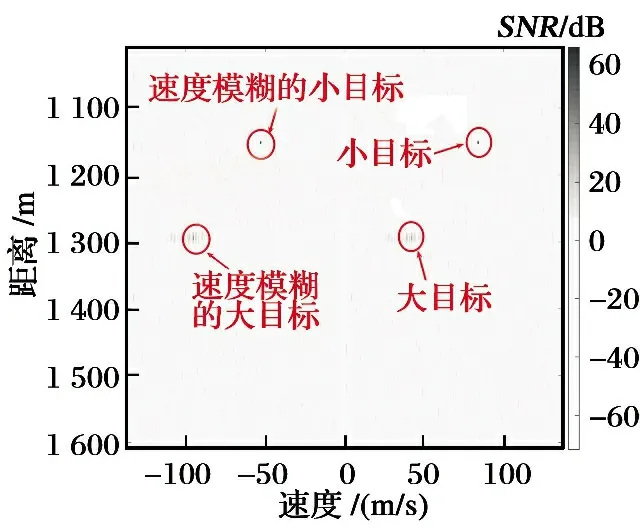
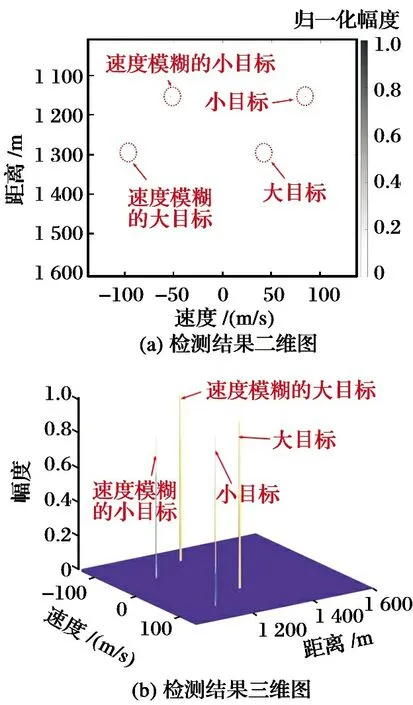
① 当2vrMTr ② 当vr>c/(4MTrB)且a ③ 当vr>c/(4MTrB)且a>c/[2B(MTr)2]时,根据式(9),目标距离走动超出了一个距离单元,且在相参积累时间内加速度使目标走动超出半个距离单元,所以目标同时出现跨距离单元和距离弯曲现象。 对于高速匀加速目标,加速度不仅会引起运动轨迹的弯曲,同时还会引起多普勒单元走动。对式(10)进行整理得 (11) 多普勒变化规律为 fdm(tm)=fd+uatm (12) 为简化运算,当目标的加速度较小时,往往忽略目标跨多普勒单元走动的影响。多普勒单元大小为1/(MTr),则目标的跨多普勒单元走动情况有下面两种情况: ①a≤c/[4fc(MTr)2]时,多普勒走动小于半个多普勒单元,加速度影响可以忽略,可直接对目标回波信号进行慢时间维FFT,实现相参积累。 ② 当c/[4fc(MTr)2] 综上所述,根据目标速度和加速度取值的不同,长时间积累方法设计需要考虑的影响因素如图1所示。 图1 长时间积累方法处理思路 Fig.1 Long-term accumulation method processing ideas 根据应用可知,对一帧即800个脉冲进行积累,则跨距离单元速度需要37.5 m/s,加速度需要3 000 m/s2,所以应用中一般不会出现距离弯曲。对于跨多普勒,需要加速度为3.4 m/s2。根据测试数据的真值可知, 大目标不会跨多普勒单元,小目标在一帧积累中可能存在跨多普勒单元的情况。 根据分析,本文提出了一种RFT和AMF融合聚焦以及LMB平滑的高精度PD雷达弱小目标检测跟踪算法。算法总体流程如图2所示,主要包括目标的检测聚焦和多目标状态估计两部分。 图2 算法总体流程 Fig.2 Overall flow of the algorithm MTI[13]通过延迟对消来消除固定杂波,常见的为2脉冲或3脉冲(即1阶或2阶)对消。3脉冲对消实际上是滤波器与慢时间上的各个脉冲进行脉冲间滤波,即做内积。阶数越高对0频附近杂波抑制越好,且不会影响周围频率信号。考虑到回波数据的相参积累脉冲数较多,本文设计了一个57阶的FIR高通滤波器来实现静态杂波剔除,其频率响应曲线如图3所示。 图3 频率响应曲线 Fig.3 Frequency response curve RFT[5]是一种优秀的相参积累方法,可以看作是广义的MTD,其统一了MTD、Hough变换和Radon变换。RFT无需对目标距离走动进行校正,通过对目标的初始位置和速度进行搜索,提取距离-慢时间二维平面中的目标观测值,之后通过离散傅里叶变换(DFT)对提取出的观测值进行积分,从而实现对目标回波能量的相参积累。所以,RFT也可以看作一组多普勒滤波器组,可根据需要将这组滤波器组的数量和系数进行改变。其定义式为 (13) 图4 RFT算法流程 Fig.4 RFT algorithm flow RFT算法在对目标回波进行相参积累的过程中,目标样本数据的提取是通过取整函数进行寻址运算提取出来的,难免存在误差,这就会使回波能量的积累受到损失,即“量化损失”。如果可以通过频域的方式实现上述变换,就可以减少通过时域寻址带来的量化损失。CZT-RFT就是在频域实现的RFT算法[9],并且由于其在频域中的对目标能量的积分可通过Chirp-Z变换在一个盲速区间内快速实现,所以其相较于RFT算法运算量大大减少,但也由于其通过Chip-Z变换实现,所以其多普勒分辨率由雷达的参数决定,不能改变。 与频域校正补偿算法类似,在频域乘以延迟指数项的共轭ej4πfVrtm/c,将t-tm平面中斜率为v的直线进行校正,最后通过快速傅里叶变换求频点fdi=2vri/λ处的能量,完成对目标能量的相参积累。整个过程如下: (14) (15) 式(14)补偿因其距离走动的相位项,并通过IFFT变换回时域,式(15)通过FFT对校正后的直线进行积累,即求取对应频点fdi=2vri/λ上的幅度。将式(14)和式(15)合并可以得到 (16) 式(16)即为频域相位补偿法的整个流程,其中,ej4πfvtm/c为频域相位补偿法中的补偿因子,ej2πft为频域相位补偿法中的IFFT。交换式(16)积分顺序可得 则式(14)~(15)变为 (18) (19) 对式(18)进行推导得 (20) 通过式(20)可以看出,将快时间频域相位补偿和慢时间相参积累结合,再进行式(19)计算,即快时间IFFT将信号变换回时域,其流程如图5所示。 图5 交换两次FFT次序信号处理流程 Fig.5 Signal processing flows for exchanging two FFT order 式(18)~(19)离散化形式为 (21) (22) 另外,式(20)采用频域相乘补偿因子补偿距离走动的方法,不会出现时域处理时因量化误差引起的能量损失,这是CZT-RFT算法的一个优点。但是,直接计算式运算量大,由于其运算过程和线性调频Z变换(Chirp-Z Transform, CZT)的形式相同,可以采用CZT进行计算,表达式为 e-jπa(k-m)2/M] (23) 其中,a是一个系数。如果a=(1-ηn), 则式(23)和式(21)完全相同。这样,式(23)可以通过CZT计算,而CZT可通过FFT实现。 CZT计算实际上是对序列x(n)的非等间隔采样,将DFT中的数字频率1/M乘以小于1的系数来调整需要得到的频率值。在CZT-RFT中,每一次CZT在慢时间序列进行,根据慢时间序列所在的快时间频点对数字频率进行调整。其原理类似于MTD,区别在于CZT-RFT是对在脉压后的快时间从时域变换到频域,再对每一频点处的慢时间序列进行CZT。 对每一慢时间序列进行CZT后,再对快时间频域进行IFFT,即可得到距离-速度二维结果,即CZT-RFT的最终结果。 基于CZT的快速RFT,在单个盲速区间内利用CZT在频域实现RFT算法(CZT-RFT),显著提高了算法的运算速度和能量积累效果,但对高速目标而言,当存在多普勒模糊时,该方法需要对多普勒模糊数进行遍历搜索并作补偿处理,然后对多次补偿后的积累结果进行选大处理,得到最终的积累结果。雷达的脉冲重复频率与目标多普勒频率关系为 (24) 自适应匹配滤波器[11](Adaptive Matched Filter,AMF)是根据广义似然比准则推导出的自适应滤波器,可有效抑制杂波,并内嵌有恒虚警效果。 二元假设检验的信号模型为 (25) 式中:y为待检测单元;yk为辅助单元,假设独立同分布;a是与传输信道和RCS有关的复数,通常未知;s为导向矢量,应用中为时域导向矢量,即 (26) 式(25)中c为杂波,服从均值为零、协方差为R的多元复合高斯分布,则两种假设下的概率分布如下: (27) 其中,(·)H为共轭转置,根据广义似然比准则: (28) 可得到滤波器输出为 (29) 其中,R的最大似然估计可通过检测单元附近的辅助单元yk得到,即 (30) 通过对导向矢量的遍历可得到每个多普勒值下的滤波结果。 AMF算法示意图如图6所示。可以看出,因为大目标距离向能量扩散,在聚焦大目标时, AMF会将大目标扩散到参考单元的信号能量认为是杂波能量,从而对大目标进行抑制,聚焦效果不好。但由于小目标距离向能量扩散较弱,对小目标聚焦的同时对周围的杂波进行抑制,可有效提高小目标对于其附近杂波的信杂比。RFT对大目标聚焦效果好,但由于小目标能量过小且信杂比提升有限,对小目标的聚焦效果不佳。 图6 AMF方法示意图 Fig.6 Schematic diagram of the AMF method 通过RFT和AMF可得到各自的聚焦结果,所以RFT和AMF各有所长,可将其结果进行融合。由于RFT和AMF的结果量纲不同,分别对RFT和AMF结果进行归一化,之后将两者结果进行单元选大,得到RFT和AMF融合聚焦结果。图7为RFT和AMF的融合聚焦结果。 图7 RFT和AMF融合聚焦 Fig.7 RFT and AMF fusion focus 将CZT-RFT和AMF的融合聚焦结果送入CFAR检测器中进行检测。本文采用单元平均CFAR(CA-CFAR[14])。CA-CFAR处理原理如图8所示,单元平均是在一系列距离和多普勒单元上进行的。 图8 CA-CFAR原理图 Fig.8 CA-CFAR schematic 被检测单元是中心单元,由于CUT可能会溢出,所以在平均处理中排除了CUT的临近单元,这些单元称为保护单元。将Nr个参考单元(在CUT的每一边各Nr/2个)的输出平均,将所有参考单元的平均估计值乘以一个常数K(用作缩放比例),就得到了门限。如果Y>KZ, 则认为CUT中存在目标。其中,K根据虚警概率Pfa和参考单元数Nr求得,程序中设置虚警率为Pfa=10-6,参考单元为Nr=36,则 (31) 其检测概率理论值为 (32) 从图9中可以得到理论值,当虚警概率Pfa=10-6,SNR≥20 dB时,Pd接近于1。 图9Pd随SNR变化理论值 Fig.9 Theoretical value ofPdas a function ofSNR 表1给出了已知的雷达系统参数。由雷达基本参数可以计算出雷达的波长为0.008 6 m,最大不模糊速度为137.14 m/s(不模糊速度范围从0~137.14 m/s),由于给定速度不超过120 m/s,因此存在一次速度模糊。最大不模糊距离为4 688 m,远大于观测场景宽度598 m,因此可以不考虑距离模糊。要求输出数据率为50 ms输出一次结果(即1 600个脉冲输出一次结果)。如果准确聚焦,50 ms的相干积累时长可以达到的速度精度为0.086 m/s,25 ms(800个脉冲)的相干积累时长可以达到的速度精度为0.172 m/s。这两种相干积累时长的精度都高于应用中给定的精度0.24 m/s(即±0.12 m/s),考虑计算的效率,本文选用相干积累时长为25 ms,也就是800个脉冲作相干积累。 表1 雷达基本参数 根据测试数据给出的真值,可知场景中存在两个机动目标,数据1~6中的时长均为2 s,目标速度和加速度(真值间隔50 ms一次)的变化范围如表2所示。 表2 目标真值变化范围 由表2可知,在2 s内,大目标的速度在-30 m/s或者40 m/s附近变化,加速度小于0.7 m/s2,可认为是匀速运动;小目标的速度在75 m/s~120 m/s之间变化,存在较大的加速度,最大值为-15.38 m/s2。 根据原理分析,若对800个脉冲进行相干积累,当目标速度大于37.5 m/s,需要考虑距离走动,加速度大于3 000 m/s2时,才需考虑距离弯曲。跨多普勒单元需要目标的加速度大于3.43 m/s2,可知大目标不会跨多普勒单元,小目标可能会跨多普勒单元。因此,对800个脉冲进行积累时,大、小目标均要考虑距离走动,不需要考虑距离弯曲。大目标不会跨多普勒单元,小目标可能会跨多普勒单元。 取表2数据1的800个脉冲进行回波分析。图10(a)为经过脉冲压缩后的原始回波,图10(b)为脉冲对消后直接FFT的二维聚焦结果,从结果中可以清晰看到大目标,而小目标则较不明显。图10(c)为脉冲对消后直接FFT的三维聚焦结果,图中可清晰看到大目标,可隐约看到小目标。需注意的是,测试数据1中小目标的信噪比相对其他数据中小目标的信噪比要高,即使这样,采用直接FFT的方法聚焦小目标的效果也很差。 图10 回波分析 Fig.10 Echo analysis 由于小目标的信噪比较低,直接FFT聚焦处理一般检测不出小目标。可以考虑对脉冲对消后的雷达数据进行RFT和AMF聚焦,得到RFT和AMF的融合聚焦结果,最后通过CA-CFAR检测器进行检测。 图11为本文方法对测试数据1第一帧数据处理的速度和距离二维图。可以看到目标位置信号的信噪比明显高于其他位置,其中,大目标不止在本身的速度位置上信噪比较高,在对应的模糊速度上也有较高的信噪比,由于模糊速度和距离不匹配可以通过跟踪去除;小目标在速度方向(对应多普勒维)由于没有估计加速度有轻微的散焦,在对应的模糊速度上也有一定的信噪比。图12为使用CA-CFAR对每个距离单元检测的结果,虚警概率Pfa为10-6。从二维和三维图中可以看到小目标可被检测出,大目标被检测出的同时在对应的模糊速度位置也出现虚警。 图11 RFT+AMF聚焦结果,各单元相对于其周围噪声的信噪比图 Fig.11 RFT+AMF focusing results, signal-to-noise ratio plot of each unit relative to its surrounding noise 图12 检测结果 Fig.12 Test results 针对雷达弱小目标的检测问题,本文设计了一套完整的聚焦-检测算法。本文算法的优势在于:RFT和AMF融合聚焦方法可以有效实现信号中强目标和弱小目标的聚焦,提高了弱小目标检测前的信噪比,从而极大地提高了CFAR检测器对弱小目标的检测概率。1.3 跨多普勒单元走动

2 基于RFT和AMF融合聚焦的弱小目标检测

2.1 动目标指示(MTI)
2.2 RFT算法

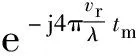
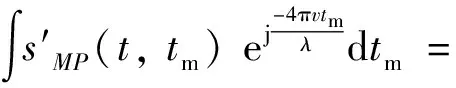
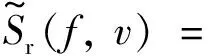

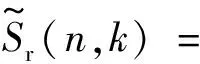
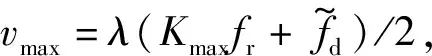
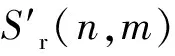
2.3 自适应匹配滤波器(AMF)
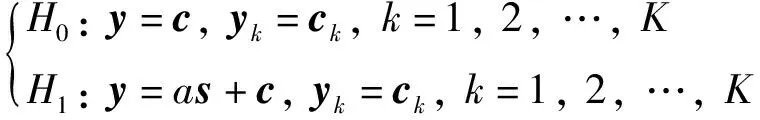
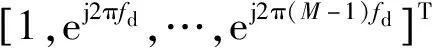
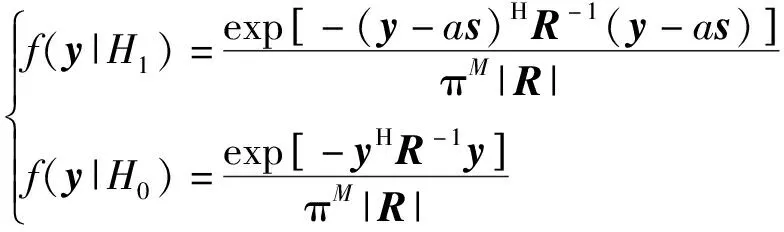

2.4 单元平均恒虚警(CA-CFAR)
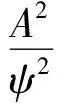
3 数据处理结果
3.1 雷达基本参数

3.2 目标特性分析
3.3 检测聚焦的结果
4 结 论
