巧用“题眼”破解压轴

韦宏 黄美玲

摘 要：“题眼”是指能够将题目中的已知条件与未知结论联系起来的关键信息。从数学解题思维过程的角度，详细说明捕捉“题眼”、关系联想、组织求解过程在中考压轴题的运用，由“题眼”联想题目的定理和性质，帮助学生提升数学思维，形成解题经验，提高解题能力。

关键词：题眼;压轴题;联想

一、数学题眼与巧用解析

数学中，何谓题眼？罗增儒教授曾指出，數学解题的本质实际上是把已知联系网与所求联系网连线起来的过程。而这条连线的交汇点就是解决问题的切入点、突破口或关键处。因此，“题眼”是指能够将题目中的已知条件与未知结论联系起来的关键信息，是题目的核心，是问题的枢纽，是问题解决的灵魂。一般地，“题眼”可从题目中的客观条件、已知结论、关键字词句或隐含的数学概念、公式、法则、定理和性质等知识点捕捉得到。

巧用，本意有灵敏、恰好之意，本文特指灵活运用某种方法，促使数学题目得以快速解答。巧用“题眼”是指根据数学的题意，围绕“题眼”展开联想、利用“题眼”产生解题思路，以便实现问题解决的过程。在教学过程中，教师若能巧用“题眼”，则能较好地抓住题目的要点，领悟数学问题的本质，顺利地解决问题。

二、巧用数学“题眼”的意义

数学解题的成功往往需围绕“题眼”展开关系联想，抓住题目要点，领悟问题的本质，找到解决问题的思路和方法。

（一）巧用“题眼”，高效解决问题

高效即快速之意，数学问题的解答，也要求有一定的速度，提高学习的效率。解数学题要先审清题意，寻找并捕捉“题眼”，然后想法设法利用题眼。巧用“题眼”，能够帮助学生快速地分清题目的主次内容，舍弃冗余的干扰信息，准确地把握问题的本质，明晰条件、结论以及问题之间的逻辑关系，打开学生解题的思路，促进其高效解题。

（二）巧用“题眼”，培养思维品质

培养学生的数学思维品质，是数学教学的重要任务。从认知心理学的角度来看，数学解题不仅是一个由表及里的心理活动过程，也是一个由现象到本质的思维探索历程。在培养学生使用“题眼”的过程中，也将经历较为复杂的思维活动过程。在教学过程中，教师指导学生对题目中的关键信息进行深入挖掘和深度解读，对有关的数学材料进行加工组织和灵活调整，以培养其思维的深刻性、灵活性和完整性。

（三）巧用“题眼”，提高数学能力

前苏联心理学家克鲁捷茨基认为，数学能力（Mathematical Ability）是指学生能较为迅速、容易并透彻地掌握数学知识、技能和习惯的那些独特的心理特征，它是一种综合素质。巧用“题眼”，要求教师要指导学生把观察到的“题眼”与已有的数学概念、基本事实等结合起来，寻找并捕捉它们的特点，归纳与概括它们的特征，发掘问题与旧知之间的启发性联系，选择和辨认所需的数学材料，进而加工组织成系统的知识系统，最终实现问题的解决。由此来看，巧用“题眼”有利于提高学生的数学发现能力、抽象概括能力和数学解题能力。

三、巧用数学“题眼”的方法

如何巧用“题眼”？解题中，要想巧用“题眼”，首先要审清题意，捕捉“题眼”。其次，调动已有的知识，回忆某些熟悉的特征，围绕“题眼”进行“关系联想”。3[3]即根据数学材料之间的一般关系、因果关系和内在联系等展开联想。例如，给出一个题目，便联想到它属于哪种题型，解决的一般方法是什么;由一个已知条件联想到相关的特征或性质;由一个定理公式联想到它的推论和应用等等。可见，关系联想就是一种调动已有的知识、回忆某些熟悉的特征、辨认所需的数学材料的思维活动。然而，在解题环节中，关系联想只是提供了问题解决的可能。因此，还需要对所收集的数学材料加以组织求解，让旧知充实或重组到原题中来，使原题得到重构、获得新的意义，实现由未知问题到已有知识的逐级递进、逐步转化和还原求解。

近年来，中考数学压轴题题目难度系数大，综合性很强，不仅注重考察学生综合运用基础知识的能力，还关注学生解题思维的探索性与创新性，巧用“题眼”，即可顺利解出压轴题。下文将以三道中考数学压轴题为例，详细分析巧用“题眼”的方法。

（一）挖掘题目内涵，由“题眼”联想定理

美国心理学家桑代克认为，一定的情境刺激与适当的反应所形成的联结构成了问题的解决。数学中，这样的“情境刺激”即为数学问题，“适当的反应”是指结论或目标，问题解决的关键则是要找到这两者之间的关系联结。数学题目中，“题眼”通常以一个字、一个词或一句话的方式来呈现。审题时，不仅要善于捕捉“题眼”，更重要的是要挖掘这些关键字、词、句的深刻内涵，理解题目的条件，认清问题的要求，深入分析已知条件与所求目标的各个元素以及元素之间的关系，利用它们之间的内在联系、因果关系等来回忆某些熟悉的概念、公式、法则、定理、性质或者数学方法，尽可能地把回忆起来的知识点用数学语言来表述出所求问题的元素，以此实现条件、目标与已有知识、经验之间的“关系联想”，从而找到解题的思路和方法。

例：（成都）抛物线与直线：交于A（1，1），B两点。若在X轴上有且只有一点P，使得∠APB=90°，求出k的值。

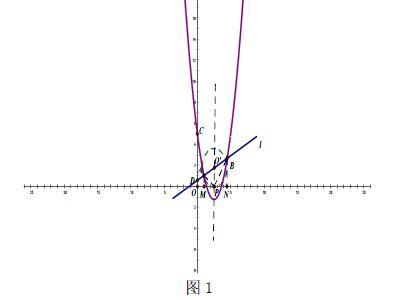
解题分析：①捕捉“题眼”：有且只有;∠APB=90°。②关系联想：可以明确这两个“题眼”构成了点P存在的限定条件，两者缺一不可。由于点P“有且只有”一个，且“∠APB=90°”，便可由合并后的“题眼”联想到切线定理。因此，以AB为直径的圆与X轴只有一个交点。③组织求解：如图1，过A，B两点添加辅助圆O，由此构造相似三角形，建立线段间的比例关系：AM·BN=PN·PM，最后，用含有k的代数式依次表示点B、点P的坐标以及未知线段，解出关于k的一元二次方程：即可。

（二）分清主次信息，由“题眼”联想性质

性质是定理的另一种表现形式，常常隐含于题干信息或解题过程中。中考压轴题的题目信息量大，客观条件足，考察的知识点较多，“题眼”的数量也不止一个，这时就需要分清主次信息，把问题的信息与认知结构的信息整合起来。根据问题所提出的目标，从复杂的回忆系统中检索出所需的理论法则或者与本问题的某些元素有联系的定理性质等。研究“题眼”时，可以将问题的条件用直观的图形、表格等表示出来，方便思考问题，产生解题思路。

例2：（2018玉林）如图2，点A，B分别为直线与X轴和Y轴的两个交点。二次函数交Y轴于点C，点P位于直线y=c上，且在第一象限内。点O是坐标的原点，连接PB，有△PCB≌△BOA。设点F是该二次函数与X轴的正半轴的交点，二次函数上的一点M位于点C，F之间（包括端点C，F），而且点M的横坐标为m。

（1）求出该二次函数的表达式;（2）当∠MPO=∠POA时，求出点M的坐标。

解题分析：（1）①捕捉“题眼”：要求抛物线的解析式，首先想到的是待定系数法。因此，需要找出位于该抛物线上的点C、P坐标。观察图象可得，点C、P分别是题目中△PCB的两个顶点。从而“△PCB≌△BOA”为本小题的“题眼”。②关系联想：围绕“题眼”，展开联想，检索所需的信息。回忆全等三角形的性质，主要有：对应边、对应线段相等和对应角相等这三点。③组织求解：在这些知识点中，哪个更适合本问题的求解呢？显然，将对应边相等这一性质“充实”到待定系数法中来，即可分别求出点C、P的坐标：C（0，4）、P（3，4）以及该二次函数的表达式为：。

（2）为本小题的“题眼”为“∠MPO=∠POA”。由图3可知，点M在二次函数上，若∠MPO=∠POA，则联想两个大知识点：全等或相似三角形中的“对应角相等”和等腰三角形中的“等边对等角”。而仅有∠MPO=∠POA和公共边OP两个条件，不易证明△POM与△POA全等或相似。此时考虑第二个知识点“等边对等角”，由此构造等腰三角形：分别延长直线PM和OA，交X轴于点Q，使得PQ=OQ。由图联想到：等腰三角形“三线合一”的特殊性质;点坐标（3，4）的特殊性（“勾股数”），则过点Q作等腰△POQ底边OP上的高QE，由此解出点Q的坐标：（）。至此，P、Q两点的坐标均已知，再联立直线PQ与抛物线的解析式，解出符合条件的点M的坐标有（0，4）或（）。

巧用“题眼”开展教学，是教师教学机智的集中体现;通过“题眼”教学，培养学生数学学习兴趣，掌握数学学习规律，不仅是新时期课程教学改革的要求，也是拓展数学课程内容边界、深化课堂教学改革的重要基础。巧用“题眼”，一般是由“题眼”联想到重要的数学概念和数学原理（公式、法则、定理和性质等）。因此，为了提高学生的“关系联想”能力，数学概念的教学不仅要让学生掌握单一的概念，还要引导学生形成一定的概念网络体系;数学原理的教学则要让学生准确地理解和记忆原理的条件和结论、熟悉原理的适用范围、掌握原理的证明方法等。总之，數学教师应努力帮助学生提升数学能力，丰富解题经验，提高数学涵养。

参考文献

[1] 罗增儒.数学解题学引论[M].西安：陕西师范大学出版社， 2001.

[2] 王成杰.题根  题眼  题感[J].高中数学教与学，2013（24）：42-45.

[3] 张雄，李得虎.数学方法论与解题研究[M].北京：高等教育出版社， 2001.

基金项目：本课题系2016年度广西职业教育教学改革研究立项项目“中职教师品牌培训项目设计、开发与实施研究”（课题编号：GXZZJG2016A138）的阶段性成果。

作者简介：韦宏（1968- ），男，广西上林人，南宁师范大学数学与统计科学学院副教授，硕士生导师，研究方向：学科教学（数学）;黄美玲（1994- ），女，广西来宾人，南宁师范大学数学与统计科学学院硕士研究生，研究方向：学科教学（数学）。