广西壮族自治区病毒性肝炎发病数的建模与预测分析

2019-02-11范晋蓉白晓东郭佩汶

质量安全与检验检测 2019年6期

范晋蓉白晓东郭佩汶白璐

（大连民族大学理学院辽宁大连 116600）

1 前言

病毒性肝炎是由多种肝炎病毒引起的以肝脏病变为主的一种传染病，它是由几种不同的嗜肝病毒（肝炎病毒）引起的以肝脏炎症和坏死病变为主的一组感染性疾病，是法定乙类传染病，具有传染性较强、传播途径复杂、流行面广泛、发病率高等特点。临床上以食欲减退、恶心、上腹部不适、肝区痛、乏力为主要表现。部分病人可有黄疸发热和肝大伴有肝功能损害。有些病人可慢性化，甚至发展成肝硬化，少数可发展为肝癌。病毒性肝炎的病原学分型，目前已被公认的有甲、乙、丙、丁、戊5种肝炎病毒，分别写作HAV、HBV、HCV、HDV、HEV，除乙型肝炎病毒为DNA病毒外，其余均为RNA病毒。己型肝炎曾有报道，但至今病原分离未成功；属于黄病毒的庚肝病毒和单链DNA的TTV与人类肝炎的关系尚存在争议。据报道，我国每年死于肝硬化和肝癌等病毒性肝炎相关疾病人数达3×105余例。因此，病毒性肝炎的预防和控制成为各级各类疾病预防控制部门的重点工作。

广西壮族自治区是我国5个少数民族自治区之一，地处亚热带季风气候区，生活环境差异大，人口增长速度较快，各类传染性疾病容易爆发。近年，随着经济不断的增强，人口流动性大幅增加，病毒性肝炎发病数也不断增长，因而病毒性肝炎的防控形势愈来愈严重。本文利用2013年1月—2019年8月广西壮族自治区甲肝、乙肝、丙肝、肝炎未分型以及全部病毒性肝炎发病数的月度数据，经过数据预处理、模型识别、参数估计、模型诊断和优化等时间序列分析手段，建立相应的时间序列模型，并对模型给出合理解释。利用构建的最优模型对广西壮族自治区甲肝、乙肝、丙肝、肝炎未分型以及全部病毒性肝炎发病数进行6期预测分析，并提出防控建议，为提高广西壮族自治区病毒性肝炎的防控提供科学依据。

2 资料与方法

2.1 数据资料

所有数据来自广西壮族自治区疾病预防控制中心（http://www.gxcdc.com/ywzd/tjxx/?from=groupmessage）。从该网站公布的数据中收集了2013年1月—2019年8月广西壮族自治区甲肝、乙肝、丙肝、肝炎未分型以及全部病毒性肝炎发病数的月度数据。

2.2 分析方法

传染病数据是典型的时序数据，因此，采用时间序列分析的方法建模。根据数据特征，利用差分整合移动平均自回归（ARIMA）模型，即求和自回归移动平均模型（Autoregressive Inte-grated Movingaverage），结合提取趋势的分析方法建模。

ARIMA模型是20世纪70年代由Box和Jenkins提出的时序数据预测方法[1，2]，其标准形式为

其中，φ（B）、Θ（B）—自回归系数多项式、移动平均系数多项式，Φ（B）=1-φ1B-φ2B2-L-φPBP，Θ（B）=1-θ1B-θ2B2-L-θqBq，εt—期望值为 0、方差值为 σε2的白噪声序列，且 E（xsεt）=0，∀s＜t；▽d=（1-B）d；B—滞后算子。模型（1）简记为：

其中，p—自回归阶数；q—移动平均阶数；d—差分阶数。趋势分析法的思想来自Wold和Cramer分别于1938年和1961年提出的序列分解原理[3]。在该思想的指导下，可把任何时序数据分解为确定性趋势部分与随机波动部分之和。

建模过程依照如下步骤：（1）数据预处理：首先，将数据整理成为可用于时间序列分析的形式，并绘制时序图和自相关图。通过时序图可初步观察数据的走势。一般地，平稳序列的时序图表现为围绕某一常数作有界波动，而自相关图表现为迅速衰减性。其次，对序列作白噪声检验。如果序列为白噪声，那么序列值之间没有相关关系。这样的序列不能用来预测，无需建模。（2）数据平稳化：首先，对具有确定性趋势的非平稳数据，提取确定性趋势项；对具有随机性趋势的非平稳数据作低阶差分，提取随机趋势。其次，对提取趋势信息之后的数据进行白噪声检验。一般地，提取趋势信息之后的数据是平稳的，可用ARMA模型拟合。但是实际操作中，如果趋势信息没有被完全提取，也会有其他情况出现。（3）模型识别：绘制平稳序列的自相关图和偏自相关图，观察拖尾和截尾的情况，估计自回归阶数p和移动平均阶数q的值。这一过程也称为定阶，其理论依据参见文献。（4）模型估计：对模型中未知参数进行估计，也称为口径拟合。（5）模型检验：首先对数据拟合的残差进行白噪声检验。如果检验结果不是白噪声，那么模型检验没有通过，就得返回（2）或（3）重新开始；如果检验结果为白噪声，那么进一步对所估参数进行显著性检验，去掉不显著的参数，获得精简模型。（6）模型优化：如果多个模型通过检验，那么依据信息量最小原则，选取最优模型。（7）预测：根据最优模型给出线性最小方差预测。

在建模过程中，使用开源软件R语言进行。

3 数据结果

3.1 数据预处理

原数据中缺失2015年3月、2015年4月、2016年5月、2017年4月和2017年11月的数据。为此，采用样条插值法，将缺失的数据补全。将甲肝、乙肝、丙肝、肝炎未分型以及全部病毒性肝炎发病数的月度数据时序化，并绘制时序图（图1）。

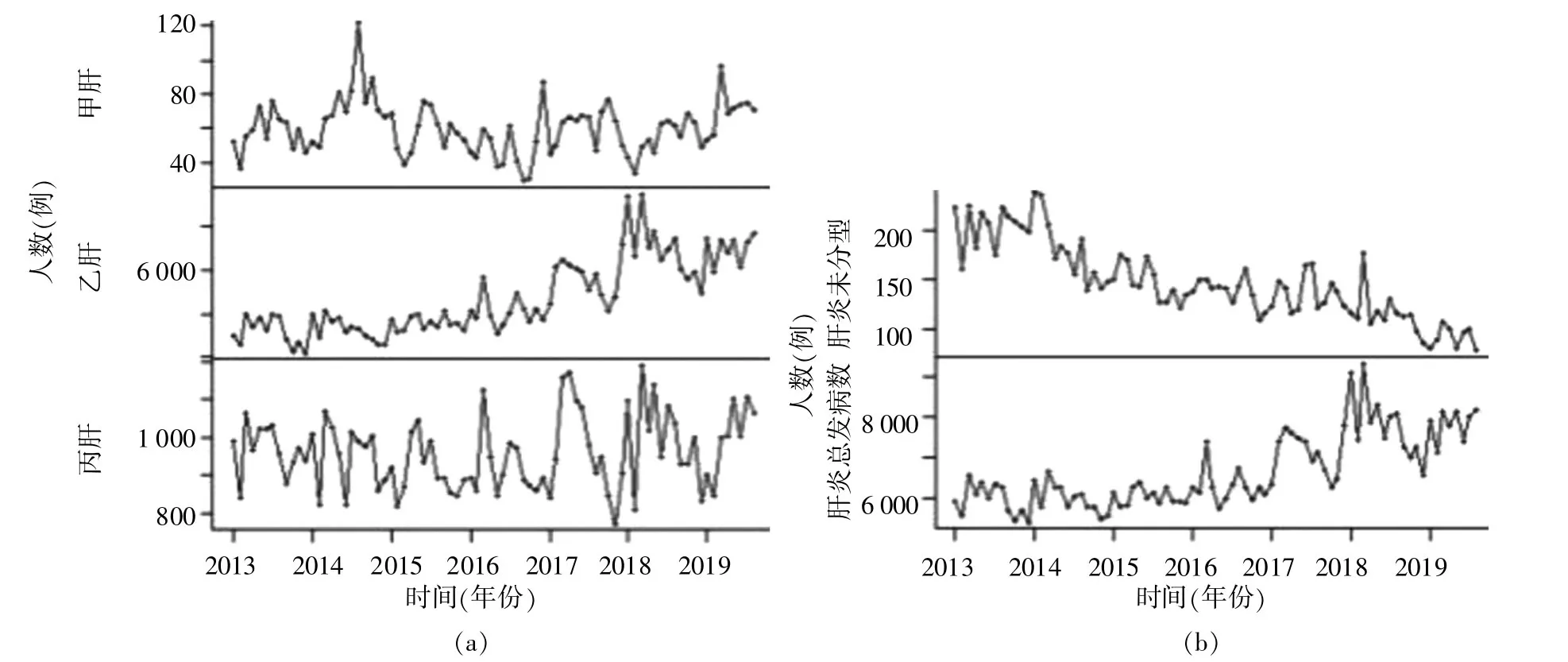
图1 时序图

由图1可知，甲肝发病数具有平稳特征；乙肝发病数具有线性递增趋势；丙肝发病数似乎具有随机性趋势；肝炎未分型发病数具有线性递减趋势；肝炎总发病数虽然主要由乙肝发病数贡献的，但异方差特征明显。

为进一步观察甲肝发病数的平稳性和丙肝发病数趋势的情况，分别绘制它们的自相关图（图2）。

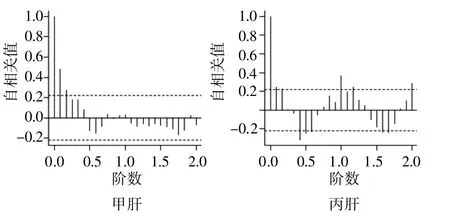
图2 甲肝和丙肝自相关图

由图2可知，甲肝发病数的自相关函数延迟2阶之后迅速衰减到2倍标准差范围之内，这是平稳序列的典型特征；丙肝发病数的自相关函数呈现出波动特征，而不具有迅速衰减的特点，因而丙肝发病数不是平稳序列。对甲肝发病数分别作延迟6阶和12阶的白噪声检验，检验的p值分别为2.09×10-5和6.58×10-4，远远小于0.05，故甲肝发病数不是白噪声，因而可以建模。

3.2 数据平稳化

分别对乙肝发病数、肝炎未分型发病数作线性拟合，详见图3。拟合结果如下：乙肝发病数：

肝炎未分型发病数:

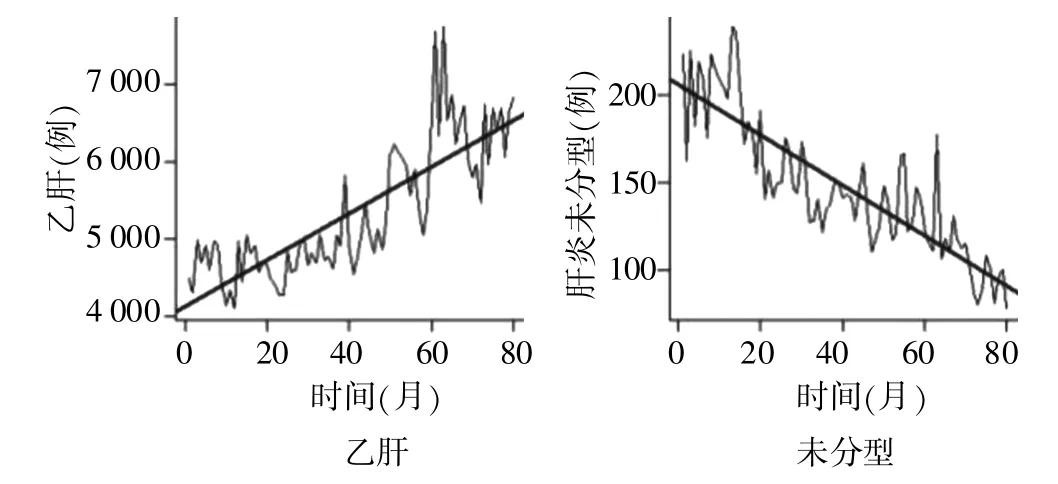
图3 乙肝线性和未分型肝炎线性趋势拟合图

图4 乙肝和未分型肝炎残差差分时序图

将肝炎总发病数的1阶差分序列平方之后，发现具有群集效应（图5），说明肝炎发病总数具有异方差特征。通过取对数，消除其异方差的特征，然后再作1阶差分，所得序列具有平稳特征（图6），最后作白噪声检验，结果表明，1阶差分非白噪声。丙肝发病数的时序图详见图7。

对丙肝发病数作1阶差分，即可消除其随机趋势。图7表明，丙肝发病数的1阶差分已经表现出明显的平稳特征。经检验，该差分序列非白噪声。

图5 群集效应

图6 时序图

图7 时序图

3.3 模型识别

甲肝自相关图与偏自相关图详见图8；残差相关自相关与偏自相关图详见图9；丙肝自相关图与偏自相关图详见图10；残差相关自相关与偏自相关图详见图11；对数相关自相关与偏自相关图详见图12。由图8可知,甲肝发病数的自相关函数具有拖尾特征，而偏自相关函数具有1阶截尾特征，因此甲肝发病数模型识别为ARIMA（1，0，0）。为了防止数据的随机性造成模型识别的偏差，可在不同视角下选择多个备选模型。为此，可提供备选识别模型：ARIMA（0，0，2）和 ARIMA（1，0，2）。由图 9 可知，乙肝波动项It（1）的2阶差分序列的自相关函数和偏自相关函数都表现为拖尾。根据拖尾特征，将It（1）模型识别为ARIMA（1，2，1）、ARIMA（1，2，2）、ARIMA（2，2，1）和ARIMA(3,2,1)几种形式。由图10可知，丙肝差分序列的自相关函数和偏自相关函数都拖尾。根据拖尾特征，丙肝发病数模型识别为 ARIMA（2，1，2），ARIMA（2，1，1）和 ARIMA（1，1，1）。由图 11 可知，未分型病发数的随机波动项 It（2）可识别为 ARIMA（0，1，1）、ARIMA（2，1，1）和 ARIMA（1，1，1）。由图12 可知，肝炎发病总数对数的差分序列自相关函数拖尾，偏自相关函数截尾，故肝炎发病总数对数的模型识别为ARIMA（1，1，1），ARIMA（2，1，0）和 ARIMA（0，1，2）。

图8 甲肝自相关和偏自相关图

图9 残差差分自相关和偏自相关图

图10 丙肝差分自相关和偏自相关图

图11 差分自相关和偏自相关图

图12 对数差分自相关和偏自相关图

3.4 参数估计、模型检验和优化

（1）甲肝发病数：分别对选定的3个模型ARIMA（1，0，0）、ARIMA（0，0，2）和 A—RIMA（1，0，2）进行“最小二乘—极大似然”口径拟合，并对残差进行白噪声检验，p值均大于0.05，认为模型都通过了检验。一般而言，R语言给出的参数估计是显著的，所以省去参数的显著性检验。若所估出的参数特别小，可通过t检验判断它的显著性，并决定是否精简。观察通过检验的模型的信息量，发现用 ARIMA（1，0，0）拟合甲肝发病数数据后所得信息量AIC=649.07，AICc=649.38，BIC=656.21，是所有拟合模型中最小的，故用模型 ARIMA（1，0，0）建模。模型如下：

（2）乙肝波动项 It（1）：使用类似(1)的做法，得到最优模型为 ARIMA（1，2，2）。模型如下：

（3）丙肝发病数：同法，得到最优模型为ARIMA（2，1，2）。模型如下：

（5）肝炎发病总数对数：最优模型为ARIMA（2，1，0）：

3.5 模型建立

（1）甲肝发病数模型已经建立，详见式（5）。

（2）乙肝发病数模型：由式（3）和式（6）联立可得，

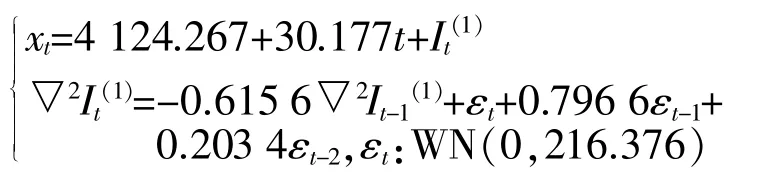
（3）丙肝发病数模型已经建立，详见式（7）。

（4）肝炎未分型发病数模型：由式（4）和式（5）联立可得

（5）肝炎发病总数模型已经建立，详见式（9）。

3.6 预测

使用建立的模型进行6期预测，给出预测的80%和95%的置信区间，并绘制预测图。

甲肝发病数预测结果详见图13；乙肝发病数预测结果详见图14；丙肝发病数预测结果详见图15；肝炎未分型发病数预测结果（2期）详见图16；肝炎发病总数预测结果详见图17。

图13 甲肝病发数预测图

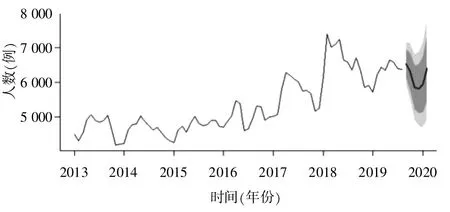
图14 乙肝病发数预测图

图15 丙肝病发数预测图

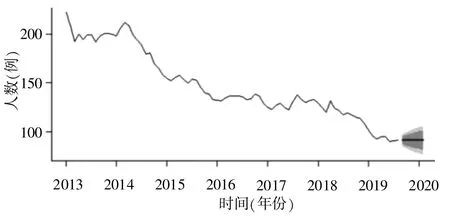
图16 未分型病发数预测图

图17 肝炎总发病数预测图

4 结果

数据表明，广西在2014年8月甲肝病发最多为122人，其余都维持在60人左右平稳波动，且模型预测结果也印证了这一点。由于甲肝传播主要依赖于日常接触、水源和食物，尤其集中爆发于人口密度大的公共场所，如学校、部队等，所以数据也表明广西城镇、农村普遍饮食卫生。乙肝病发在广西较多，而且有递增趋势。特别在2018年1月和3月乙肝病发数达到7 620和7 744人。预测结果表明，2019年9月—2020年2月，每月病发数都是6 000人左右。建议当地疾病防控工作重点放在血源性传播，医源性传播，母婴传播，生殖细胞传播，密切接触传播（性接触为主），吸血昆虫（蚊子，臭虫等）传播上。丙肝发病数的特点是波动比较大，特别是2017—2018年波动最为剧烈。丙肝的主要传播途径是血液传播、性传播和医源性传播，因此，防控重点是医疗卫生机构和性教育。肝炎未分型病发数呈递减趋势，1期预测值仅为90。这说明，广西医疗条件逐年改善，肝病化验医疗水平不断提高。病毒性肝炎至少有甲、乙、丙、丁、戊型5种，前面只分析了甲、乙、丙型，而肝炎发病总数中包含了全部病毒性肝炎发病数。从整体看，病毒性肝炎发病总数呈现递增状态，而且2017年和2018年还出现过爆发。从预测情况看，这种增长趋势在加强。因此，广西壮族自制区病毒性肝炎预防和控制工作形势严峻。