利用“数形结合”培养小学生“数感”的策略

江苏连云港市灌云县新区实验小学 于家波

《义务教育数学课程标准（2011年版）》指出：“应当注重发展学生的数感。”培养小学生的数感，也就是提高他们对“数与数量”“数量关系”“运算结果估计”等方面的感悟。建立“数感”对于提高学生对数量的悟性和计算结果的准确性，培养学生的逻辑思维能力至关重要。因此，小学数学教师在教学中应高度重视对学生“数感”的培养。培养小学生“数感”的方法有很多，其中最常用、普适性最强的就是“数形结合”法。下面笔者结合教学实际，谈谈利用“数形结合”培养小学生“数感”的几种具体做法。

一、利用实物、图形的直观教学，培养数感

在小学数学课堂上，利用实物或者图片进行直观教学，是教师常用的数形结合方法，可以帮助学生建立直接的数感，还可以帮助学生理解数学概念。

1.把数字形象化

直观教学法在低年级使用得比较多，因为数字对于低年级小学生来说只是一个个抽象的符号，教师需要借助直观教具的演示，帮助学生把抽象的数字与实物或图形建立实际联系，从而把数字具体化，形成固定的思维意识。

例如，在教一年级学生认识数字时，笔者先用小棒在教具上摆出一定的形状，比如数字“2”就用两根木棒摆出“一双筷子”，数字“3”就用3根小棒摆成一个三角形，数字“4”就用4根小棒摆成一个正方形……然后让学生在自己的课桌上用小棒分别摆出与相应数字对应的形状。这样做，巧妙地把数形结合起来，让抽象、呆板的数字变得具体可感、生动鲜活，使学生在脑海里建立了对数字的具体表象，加强了学生对数字的思维定式。

2.把概念直观化

在引导中高年级学生认识分数、小数和一些几何图形与几何体时，就更离不开直观教具和图形的辅助了。

例如，教学《认识分数》时，可以把写真图形与会意图形相结合帮助学生理解分数的内涵，建立对分数的数感。如下图：把一个蛋糕平均分成2份，每份是它的；把这个蛋糕平均分成4份，每份是它的；根据图意，＞，也就是说分子相同，分母大的分数反而小……如果没有具体的图形作为参照，任凭教师费尽口舌学生也无法理解同分子分数的这一特点，有了具体图形的帮助，学生理解起来就非常容易了。

利用实物或图形进行直观教学，是帮助学生认识分数和小数的意义、建立几何形体概念的最佳途径。教师可以利用图形引导学生一步步分析分数、小数的内涵，培养学生对分数、小数的数感；可以借助图形的变化推导出各种几何体的面积和体积计算公式，帮助学生在“实物、图形”与“数字、概念”之间建立起对应的数量关系，一方面培养了学生的数感能力，同时也提高了学生的空间思维与逻辑思维能力。

二、利用在数轴上表示数，培养数感

把“数轴”与“数”相结合，引导学生在“数轴”上认识“数”，可以帮助学生建立各种“数”的概念，进而培养学生的数感。

1.帮助学生建立数字的概念

对于低年级小学生来说，数字符号与它们所代表的意义是分离的，也就是说，他们在念“1、2、3……”时就像鹦鹉学舌一样，只是在机械地模仿和重复，并不懂得这些数字表示的内涵。因此，教师除了要借助直观教具，还可以利用数轴帮助低年级学生建立对数字的概念。

例如，教学《20以内数的认识》时，笔者先引导学生用小木棒摆出20以内的各个数字，然后再把20以内的数字在数轴上直观展示出来，如下图：

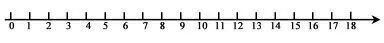
这样，学生就能从数轴上直观感受到数字的大小与排列顺序，就会把抽象的数字与数轴上具体的点联系起来，从而在脑海里建立清晰的数字概念。

2.帮助学生理解分数、小数的意义

分数和小数的意义对中高年级的小学生来说既拗口又抽象，尤其是分数、小数的大小比较，更是把学生弄得头晕目眩。如果把分数或小数在数轴上表示出来，就变得一目了然，学生就很容易判断出分数与小数的大小，从而真正建立对分数、小数的数感。例如，在数轴上可以这样表示，如下图：

这样，各个分数的大小及排序在数轴上展示得清清楚楚，学生很容易判断哪个分数大，哪个分数小，哪些分数是相等的。

再如，用直线上的点表示下面的小数，并比较每组数中两个数的大小：

0.1和0.08 0.4和0.04 0.29和0.31

如上图，通过观察数轴，学生很容易判读出0.1＞0.08，0.4＞0.04，0.31＞0.29。

笔者在教学实践中发现，利用直线上的点来表示各类数字（如整数、分数、小数等），可以把抽象的数字直观形象化，帮助学生建立数的概念、理解数的意义，提高学生对各种数字的数感。

三、利用线段图理清数量关系，培养数感

利用线段图理清数量关系，是指画一条或者几条线段来表示题目中的数量关系，让题目中的数量关系直观化、清晰化，帮助学生找到解题思路，从而顺利解决数学问题。在小学低段，很多应用题的数量关系比较简单，学生通过认真读题与思考就能理清题中的数量关系；但随着学生的年级不断升高，应用题的难度不断加深，题目中的数量关系也逐渐变得复杂，借助画线段图分析数量关系，既可以帮助学生找到解题思路、简化解题过程，也能不断提高学生的分析与推理能力。

画线段图解应用题有四个步骤：（1）找出题中的条件与问题；（2）用线段图表示数量关系；（3）根据线段图找出解题思路；（4）根据解题思路列式解题。

下面结合教学实际具体谈谈如何画线段图解决数学应用题。

1.找出题中的条件与问题

首先出示题目，让学生仔细读题，理解题意。

小建和小西买同样的笔记本，小西买了5本，小建买了3本，小西比小建多花12元。每本笔记本是多少元？

接着，让学生找出题目中的已知条件和未知问题并标记出来。题中的已知条件有四个，其中三个是数字条件：小西买了5本练习本，小建买了3本，小西比小建多花12元；一个是文字条件：小建和小西买同样的笔记本。题中的问题是求“每本笔记本是多少元”。

2.用线段图表示数量关系

题目中的条件和问题找出来后，就要引导学生把这些数量在线段图上表示出来：3本笔记本可以在线段上用3份表示；5本笔记本可以用5份表示；由于小西和小建买的是同样的笔记本，因此两条线段每份的长度相等，如下图：

这样一来，就把题目中的数量关系在线段图上直观地展现出来了。

3.根据线段图找出解题思路

从上面的线段图来看，小西多花的12元实际上就是比小建多买的笔记本的钱。因此，要求每本笔记本是多少元，只要先求出小西比小建多买了几本笔记本，再用12除以多出的本数，就是每本笔记本的价钱。

4.根据解题思路列式解题

既然解决问题的思路找到了，那么接下来的列式计算就是水到渠成，问题自然也就迎刃而解了。

教师在指导学生画线段图解决实际问题时，要注意以下几个问题：

（1）线段图上要标示出题目中所有的已知条件及问题；（2）要一边思考数量之间的关系一边画图，而不是画完图再去分析数量关系；（3）可以根据线段图用不同的思路解决问题，鼓励学生一题多解；（4）要把得数代入原题进行检验，引导学生学会验算与反思。

分析应用题的数量关系既是小学应用题教学的重点，也是应用题教学的难点，利用线段图分析数量关系、找解题思路，无疑是为学生解应用题插上了“双翼”，让那些纷繁复杂的数量关系变得直观明朗，使学生在解决问题的过程中充分体验到数学探究的乐趣，体会到自主解决疑难问题的成功与喜悦，这对于激发学生的数学学习兴趣、增强学生的数学学习自信心都大有裨益。