启“思”传“慧”：让核心素养在课堂上生根发芽——“圆的再认识”教学赏析

江苏南京市东山小学 李一婷

一、初识“传慧”其人

第一次见到穆传慧老师是在“百师万课”的舞台上，他执教的内容为“圆的再认识”。

正如其名，传慧老师慧心妙语，课堂上从容不迫、游刃有余，细细揣摩，每一句话语都蕴含深意、智慧无比，从简短的“课前三问”就可见一斑——

片段1：课前交流第一问

师：你会用话筒吗？

生1：我会用。

师：那么你们会用吗？这位同学，你说一下你会用话筒吗？

生2：会。（学生回答声音很小）

师追问：大家说会不会啊？声音太小了靠近一点。

生2：我会。

师：哎！这就好，这叫真会。

片段2：课前交流第二问

师（第二个问题来了）：你会鼓掌吗？

生：会。

师：什么时候鼓掌？你说。

生1：我会在有人发言，回答的好的时候热烈鼓掌。

生2：就算发言不好也要鼓掌鼓励。

生3：就是在所有同学做得好，值得去表扬的地方，要鼓掌。

师：好的，只要他思考了而且他遇到困难时不放弃，这时候更需要表扬。对不对，是吗？掌声可以给自己和同学。

片段3：课前交流第三问

师（第三个问题）：你会学吗？你会学习吗？生：会。

师：因为这是我们每天都在干的事，是不是？

生1：对，而且学习就是我们生活里一个很重要的事情。如果没有它或许我们也没法这样快乐。

师：她说学习是快乐的。你看掌声就来了，果然会鼓掌。

生2：因为我们是学生，学习就是我们的天职。

师：名人名言都出来了。那么，老师想告诉大家，有一种学习叫作“教”。你有感觉的时候你不要坐在座位上，你可以到前面来，像老师这样，和大家交流。来跟我说，有一种学习叫作——

生：教。

短短几分钟时间，穆老师迅速和学生打成了一片，在不知不觉中，他已经向学生传达了数学学习和数学课堂应有的姿态，带领学生逐步进入“一场惊天动地的享受”之中……

二、赏析“传慧”课堂

2016年9月发布的《中国学生发展核心素养》中提出：中国学生发展核心素养分为三个方面，即文化基础、自主发展和社会参与。文化基础又分为两种具体的素养——人文底蕴和科学精神。在穆老师的课堂上，科学精神与人文底蕴两者并举并重，真正让学生的核心素养得以“生根发芽”。

1.紧扣合情推理，力求科学实证

穆老师善用“问题”来激发学生进行深度探究。在这节课中围绕圆周长公式的推导他提出了三个问题，带学生经历了三个层次的理性思考和探究活动，让学生的猜测与推理都建立在科学思考与辩证推断的基础之上。

第一层次：周长与什么有关？

课始，穆老师从学生已有的经验——多边形的周长入手，引领学生逐步回顾了正多边形的周长。

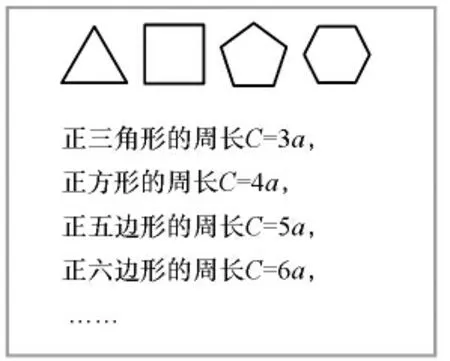
而后穆老师引领学生观察，感悟“什么变了？什么没变”，让学生体会到“边长会变，周长也会变，而周长与边长之间的倍数关系不会变”。之后，穆老师不断增加多边形的边数，让它越来越接近于圆形，给予学生视觉上的直观冲击——“圆的周长与近似多边形的边数有关，成倍数关系”。但是圆的周长与圆自身的什么因素有关呢？穆老师又启迪学生展开第二个层次的思考与探究。

第二层次：圆的周长与什么成倍数关系？

穆老师紧接着依次呈现了两幅图（如图1、图2），引导学生思考两个问题：（1）如果在正方形内画一个最大的圆，很显然正方形的边长就是圆的直径，那么正方形的周长是直径的多少倍？（2）如果在圆内画一个正六边形，这个六边形的周长又是直径的多少倍？学生由直观图轻松地发现“正方形的周长是圆直径的4倍，正六边形的周长是圆直径的3倍”。那又如何解决“圆的周长与正方形周长、正六边形周长、圆直径的关系”呢？穆老师提议“来合个影”!由此得到了图3，难题一下子迎刃而解：圆的周长比它直径的4倍（正方形周长）小，比直径的3倍（正六边形的周长）大。

图1

图2

图3

第三层次：圆的周长与直径成几倍关系？

圆的周长到底是直径的几倍呢？穆老师设计了一系列的测量和计算的活动：

（1）团队合作，测量一个瓶盖的周长和直径，计算周长与直径的商。

（2）想办法画出一个圆的周长和直径，测量后计算周长与直径的商。

（3）测量同一个圆的外接正六边形和内切正六边形（如图4）的周长与直径，计算周长与直径的商。

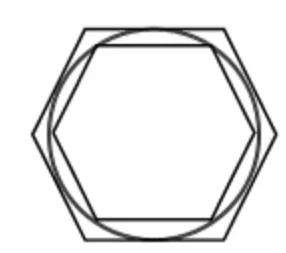
图4

图5

（4）测量同一个圆的外接正十二边形和内切正十二边形（如图5）的周长与直径，计算周长与直径的商。

学生通过一次又一次的测量、计算、反思、调整等活动，使周长与直径的倍数关系逐步精确，在这个过程中，穆老师抓住关键，“见缝插针”，引发学生的思考走向更深层次。如“车轮三兄弟”中周长与直径长度的直观比较、刘徽“割圆术”的引入，从而让学生的科学精神在数学课堂中得到有效培养。

“科学精神主要是学生在学习、理解、运用科学知识和技能等方面所形成的价值标准、思维方式和行为表现，具体包括理性思维、批判质疑、勇于探究等基本要点”，这些都在穆老师的课堂上得以落实。通过实事求是的度量，借助度量过程中的误差，培养学生求实的科学精神；通过同伴协作和实践活动，在对话、质疑、思考中培养学生刨根问底的探索精神和严格精确的思维习惯，让学生真正经历数学知识科学探索与求证的过程，让学习在每个学生身上都真实地发生，这样的经历对学生来说是生动而又深刻的，是他们学习生涯中最宝贵的财富，也是他们可持续发展的基础。

2.史料贯穿研究，文化浸润儿童

数学课程标准指出：“数学是人类的一种文化，它的内容、思想、方法和语言是现代文明的重要组成部分。”作为一种文化，数学有着其独特的历史积淀、文化情怀以及审美情趣，如何在数学课堂教学过程中渗透数学文化，让文化浸润学生的数学学习过程？穆老师给我们做了极好的一个范例。

如“割圆术”教学片段：

师：圆的周长差不多是直径的三倍多一点。你们知不知道数学家们怎么算周长？其实历史上很多人做过。比如刘徽的“割圆术”：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣。”你是怎么理解的？

生：在割圆的时候一圈一圈的就是让里面图形的边数增加，到最后增加不了了，它就是一个圆。

师：他懂了，如果我再配上这个图，你懂了吗？现在我要问你，我在圆里画正六边形、正十二边形、正二十四边形越画越多，割之又割，以至于不可割，则与圆合体，而无所失矣。现在懂了吗？想不想试一试？我们屡败屡战！

一课尽显其知识之广博。穆老师有着丰富的与数学内容有关的数学史话和数学故事，当和学生进行交流讲到相关内容时，引经据典、旁征博引，随时插入对学生进行数学文化的人文价值教育，如阿基米德洗澡的故事、爱迪生的100次失败，用通俗易懂、平实感人的故事感染学生。在介绍古今中外数学家研究圆周率的历史过程时，穆老师更是侃侃而谈、信手拈来。从“周三径一”到阿基米德，从祖冲之到鲁道夫，乃至现代数学家利用计算机计算出圆周率是一个无限不循环小数……在这一过程中，穆老师将数学史料和数学知识紧密结合，使学生经历知识形成过程的同时感受到数学文化以及科学家们严谨的研究态度。正如穆老师在课尾给予学生的谆谆教诲：“圆周率π的小数位数是无穷无尽的，也意味着我们对真善美的追求应该也是无穷无尽、永无止境的。”这样一种数学学习的过程，学生感受到数学学习的乐趣，领悟到数学知识的丰富、数学方法的精巧、数学思想的博大、数学思考的美妙，那么，数学的文化价值显露无遗。

南开大学数学科学学院顾沛教授曾说过：“十三年的数学学习后，那些数学公式、定理、解题方法也许都会被忘记，但是形成的数学素养却终身受用。”是啊，尽管我们大部分人在一生中至少要经历长达12~13年甚至更多年的数学学习，但几乎都错误地认为学数学就是为了解题、考试，而不了解数学在实际生产生活中的应用，更谈不上数学学习对其思维方式和习惯的影响。那么，数学教学到底要让学生学到什么？这是值得我们所有数学教师深思的问题，穆老师的课堂也让笔者“一梦惊醒”，我们在不遗余力地“教”的同时，该放宽自己的视野，聚焦儿童的人文底蕴和科学精神的培育，使得学生的核心素养真正落地、生根、发芽。