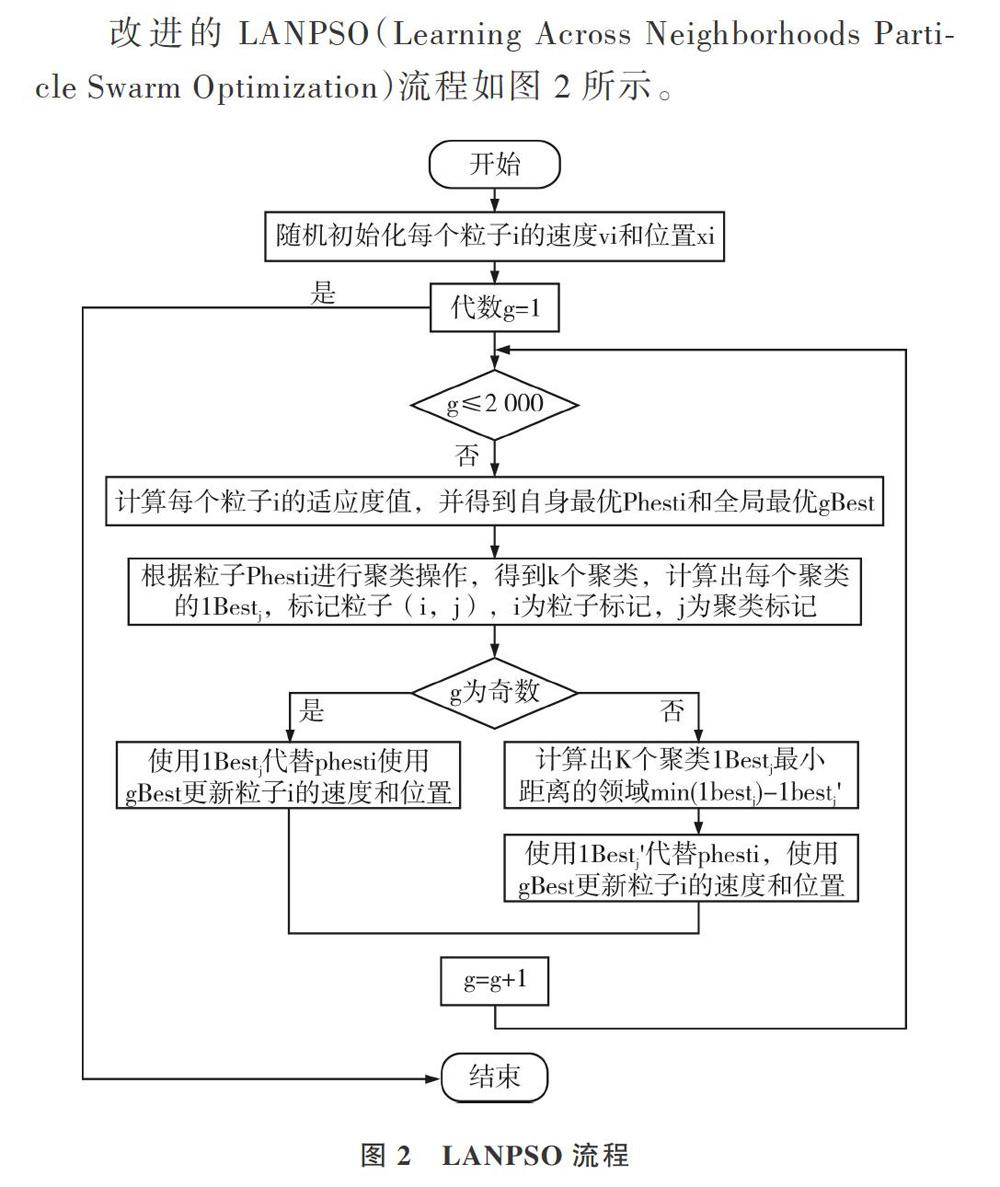
一种跨邻域学习的改进粒子群优化算法

唐懿芳 钟达夫 杨叶芬

摘要：为了改善传统粒子群优化算法过早陷入局部最优解的缺点，进一步增强算法收敛性，通过使用一定范围内邻域最好位置1Best代替自身历史最好位置pBest进行速度与位置更新，以增强粒子跨邻域学习能力。使用整个群体中最好位置gBest进行速度与位置更新，可增强算法收敛性，且具有较好的全局搜索能力。在8个不同的单峰和多峰函数上系统地对3种算法进行测试与比较，实验结果表明，提出的跨邻域学习改进粒子群优化算法可避免粒子群陷入局部最优解，求解精度与算法收敛性都提升了15%以上。

关键词：粒子群优化算法;跨邻域学习;局部最优;加速收敛

DOI：10.11907/rjdk.191162

中图分类号：TP312 文献标识码：A 文章编号：1672-7800（2019）012-0122-04

0引言

美国心理学家Kennedy和电气工程师Eberhart在1995年通过模拟鸟群或鱼群等群体觅食行为而提出的粒子群优化算法（Particle Swarm Optimization，PSO）是一种群体协作的随机搜索进化算法。该算法从随机解出发，通过捕获当前搜寻到的最优值，不断循环迭代寻找到全局最优解，并使用适应度函数值评价解的质量。该算法实现较为容易，已被成功应用于多个领域，尤其在各类智能优化问题方面应用广泛。

但PSO研究中一直存在两个待改进的问题：加速收敛与容易陷入局部最优。为解决以上问题，研究人员对算法进行改进，改进方案主要有：对惯量系数的改进、增强多样性的改进、拓扑结构改进，以及协同其它优化算法混合改进等。这些方法对粒子群优化算法的性能都有一定提升，但截至目前，针对上述两个问题，仍有较大改进空间。

本文所讨论的改进粒子群优化算法是基于当人们行为倾向于朝同伴方向变化时，会逐步趋同，比较容易陷人局部最优解，如果其学习别的邻域最优解，则会对容易陷人局部最优的问题有一定改善。同时算法选择邻域最优值学习要在一定范围内，不能选择较远的领域学习，因此比目前的粒子群优化算法易于收敛。

1粒子群优化算法改进基本思想

最开始通过随机产生一定规模的粒子作为问题搜索空间的有效解，这是粒子群优化算法的惯常步骤，然后进行迭代搜索得到优化结果。由于粒子群优化算法具有简单易用、高效实用的特点，自提出以来，众多研究者对其进行了探讨与改进，并且在越来越多的领域得到运用。

但Trelea在2003年指出，PSO最终稳定地收敛于空间中某个点，并不能保证收敛到全局最优点，甚至不一定是局部最优，而是过早停留在一个当前最好的点上。为了提高PSO算法性能，以Eberhart&Shi为代表的研究者提出3个方向：①算法参数研究;②拓扑结构研究;③混合算法研究。

算法参数研究是指PSO具有惯量权重ω、加速系数c1与c2、最大速度、种群规模等参数，参数分析试图通过研究这些参数对算法全局搜索能力与局部搜素能力的影响，找到更好的参数配置或自适应调整方案，提高算法性能。

拓扑结构研究是指PSO有全局版本与局部版本之分，其不同之处在于更新速度时采用整个种群最优的粒子作为样本，不同拓扑结构会影响算法局部搜索与全局搜索能力。本文重点针对拓扑结构的改进进行研究。

混合算法研究是指基于PSO自身收敛速度快，但容易陷人局部最优的特点，混合算法引入进化算法中的相关算子，例如选择、交叉、变异等算子，或者其它增加算法多樣性的技术，以提高算法性能。

2粒子群优化算法拓扑结构改进思路

粒子群算法拓扑结构也称为社会结构，是指算法中的个体如何进行相互作用的问题。群体中的每个个体都在相互学习，除基于自身的认知外，还在不断地向比自己更好的邻居移动。通过这样的信息交流，整个群体能够聚集到一个全局最优位置。本文针对在复杂问题中PSO表现出更好性能、更能避免陷入局部最优的特点，主要针对拓扑结构算法进行改进。

为了改进PSO过早陷入局部最优的缺点，PSO有全局版本PSO（Global Version PSO，GPSO）和局部版本PSO（Lo-cal Version PSO，LPSO）。在GPSO中，整个群体构成一个“社会”，即粒子在进行速度与位置更新时，将会使用自身的历史最好位置pBest与整个群体中的最好位置gBest作为更新向导。在LPSO中，每个粒子所处的“社会”仅是一个小的领域，除使用自身的历史最好位置pBest外，粒子在进行速度与位置更新时还要使用领域中的最好位置1Best作为参考。可见，LPSO版本中能够用作更新向导的位置要比GPSO更加多样化（因为在LPSO中每个粒子对应的1Best很可能不同，而在GPSO中的gBest都是一样的），所以LPSO的多样性更好，在处理复杂问题时会表现出比GPSO更优异的性能。GPSO和LPSO中的粒子更新示意图如图1所示。

相关研究表明，人们的信仰、态度与行为一般趋同，即人们行为会受到身处群体的影响，人们会模拟自身所在群体的典型行为。但如果一味拘泥于自己群体的最优值，比较容易陷入局部最优。为了避免固定邻居的不足，用别的领域的最好值进行学习，可在较大程度上避免出现局部最优问题。

文献[17]使用簇分析改进算法性能，具体实现过程为：首先将整个粒子群划分为几个簇，确定簇中心，然后用个体i的簇中心CLUSI代替pBest，或用目前找到的最优个体g的簇中心CLUSG代替gBest，用于进行粒子速度和位置更新。其采用带收敛因子的粒子群优化算法进行实验，实验结果表明，用CLUSI代替pBest可显著改善算法性能，用CLISG代替gBest则会降低算法性能，这也显示了增加算法多样性效果的两面性。

社会心理学研究也表明，当人们行为倾向于朝同伴方向变化时，其互相之间会有一个潜移默化的作用，即逐步趋同，也即容易陷入局部最优解。如果他们跳出圈子，学习别的邻域最优解，对粒子群优化算法容易陷入局部最优的问题则会有一定改善。选择邻域最优值学习要在一定范围内，不能选择较远领域学习，这样不容易收敛，应选择一定距离范围内的邻域，相当于遗传算法变异过程。设定合适的变异因子，小于变异因子的适应值才能进行变异，形成多样化的结果。

基于以上分析，本文改进算法思路是，基于增强多样性、避免陷入局部最优的原则，在粒子更新速度和位置时，不用本领域的最优值，而用与粒子群本身领域lbest最小距离范围内别的领域的最优值lbest'进行学习。即：

循环过程中，每隔一代就采用聚类方式，得到最近邻域进行学习，使粒子不会过早陷入局部最优，而用全局最优gBest更新位置和速度，可保证粒子尽早趋近于全局最优。

3实验测试与结果

3.1基准函数说明

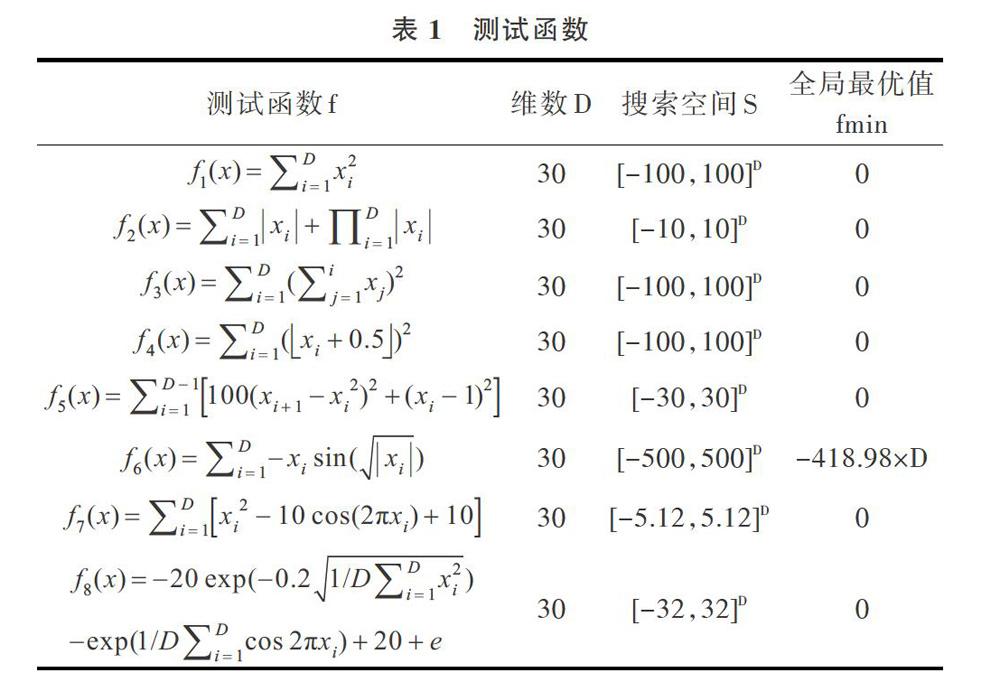
为了验证改进算法的有效性和高效性，本文采用8個标准测试函数进行测试。8个基准函数都是用来测试算法性能的典型函数，如表1所示。对于每个测试函数，通过进化过程中的每一次迭代对函数进行优化。

表1列出了用于实验测试的函数，这些函数可分为两组，前4个是单峰函数，后4个是多峰函数，其中多峰函数存在多个局部最优解。另外，在表1中还给出了测试的基因维数D（第2列）、基因数据搜索空间（第3列），以及该函数对应的全局最优值fmin（第4列）。

由于改进算法会多次调用适应值评价函数，而调用适应值评价函数对系统资源量消耗较大，因此为了公平地与其它算法进行比较，所有算法都采用最大适应值评价次数2000作为循环结束条件。同时，为了减少统计误差，各算法在每个函数上测试30次，分别取最优值、平均值、最差值进行比较。

3.2结果比较与分析

实验结果采用经典的PSO算法、Lin提出的分层改进粒子群优化算法HSPPSO（A Hierarchical StructurePoly-Particle Swarm Optimization）与本文提出的LANPSO算法作比较。3种算法在单峰函数f1和f4的比较结果如图3、图4所示，在多峰函数f7和f8的比较结果如图5、图6所示。

在一定范围内的邻域学习有更精细的局部搜索能力，如果粒子与全局最优位置相距较远，则收敛速度较慢，但本文提出的LANPSO算法仍能较快收敛。

图5、图6显示在多峰函数f7和f8中出现较早收敛，使用跨领域学习方法可以增强算法多样性，不容易过早陷人局部最优。

实验结果表明，无论是单峰函数还是多峰函数，本文提出的LANPSO算法在收敛性和多样性方面都得到了一定程度改善。

4结语

为了解决粒子群优化算法收敛速度慢与容易陷人局部最优的问题，本文提出一种基于跨领域学习的改进粒子群优化算法。该算法在粒子更新速度与位置时，用与粒子群本身领域lbest最小距离范围内别的领域最优值lbest'进行学习，避免了过早陷人局部最优，在一定程度上平衡了算法的局部搜索能力与全局搜索能力。通过对8个基准函数进行测试对比，实验结果表明，本文提出的改进算法收敛速度快、求解精度高，对大多数函数都能避免陷入局部最优，因此对粒子群优化算法性能有较大提升。下一步研究重点主要集中在如何应用LANPso算法降低无线传感器网络能耗方面。