初中生数学理解力弱化的现实解读与教学修正
2019-02-06张兆驹
张兆驹

摘要:由于初中数学八年级教材知识点出现断层,内容难度大,学生阅读能力转化不力,逻辑思维不够严谨,心理调节能力不强以及创新思维匮乏等原因,造成了学生数学理解力弱化的现象。为此,教师在教学时应注意:加强知识点勾连,形成数学知识链条;注重阅读力培养,提高数学审题能力;提升逻辑思维水平,提炼数学思想方法;关注情绪化体验,树立数学学习自信;创新教学手段,提升数学学习效能。
关键词:理解力;数学阅读;数学知识;教学修正
中图分类号:G633.6 文献标志码:A 文章编号:1673-9094(2019)12A-0075-05
与七年级相比,八年级的数学内容无疑增加了广度和深度。随着孩子年龄的增长,自我意识的提高,学生对于获得尊重、享受平等的意愿也明显增加,但对于数学课堂知识的深化没有较好的心理准备,产生了一定的认知和心理冲突。
数学理解力就是运用数学知识来解决生活实际的问题,是数学学科的价值和功能的一种体现,也是培养能力,提升素养的一个重要方面。数学理解力已成为考察学生数学学习力的一个重要方面,但由于初中生正值“身心剧变”时期,其中八年级学生尤为明显,美国心理学家霍林沃斯称之为“心理性断乳期”。甚至有人认为八年级是整个中学阶段“最危险”的阶段,他们最难管理,被称之为“八年级现象”[1]。因此,在学习过程中,学生的数学理解力出现了逐步弱化的现象。
一、初中生数学理解力弱化的现实解读
数学理解力主要是指学习数学时的阅读能力、书写解题过程的能力、整体思考的能力、观察问题的能力等。本文参照苏科版教材,根据教学实践情况以及调查问卷分析,归纳出八年级学生数学理解力弱化的原因。
1.知识点出现断层,增加了学习数学的难度
对于七年级学生来说,由小学学习中应用题的计算延伸到七年级的方程,自然而流畅;由小学学习的特殊图形的认识延伸到七年级的平面图形的认识,熟悉而亲切。而当进入八年级时,学生学习函数时,对知识的理解很显然出现了断裂,特别是变量关系的寻找,抽象性很强,学生往往产生畏惧心理,也就不太容易把握知识点的横纵联系。学生对于七年级的平面图形的认识也仅局限于零散的、碎片化的知识结构。而到了八年级,要求学生把零散的知识有条理地组织起来,再借助性质特点把因果关系表达出来,条理化要求较高,学生再一次遇到了瓶颈,造成了学生表达困难,甚至听不懂的现象。
2.阅读力转化不力,影响了学习数学的效度
数学阅读力关键体现在数学语言(文字语言、符号语言、图形语言)间相互转化的能力[2]。而八年级学生阅读数学材料时往往不能静心,一目十行,缺少分析思考,结果对材料的理解不深不透,时间一长甚至会失去阅读兴趣。笔者抽查了八年级的期中、期末考试试卷,经过统计分析,发现不少学生在阅读量较大的题目上的得分整体不高,特别是对于知识点的概括提取和运用时会和题目要求有偏差。通过回访一部分学生,得出的原因是学生认为数学阅读耽误时间,所以只抓要点,但往往忽视前后的联系。
3.逻辑性不够严密,影响了学习数学的深度
八年级的学生条理化水平不高,在解答完题目后缺少总结的意识,更谈不上规律的概括和思想的提升。学生很难形成对某一数学类型的深入理解,更谈不上迁移运用了。在笔者批改一道勾股定理题目时,出现了这样的情况:
题目:直角三角形的两条边长分别为6和8,那么这个直角三角形的第三边长为 。有一部分学生的解答是这样的:由勾股定理得,该直角三角形的第三边10。这里学生首先会受勾股定理中常见的勾股数6、8、10的影响,不假思索地把6、8當作直角三角形的两条直角边,从而得到上述错误的结果。其次,学生已经做了较多勾股定理公式的运用练习了,但还没有真正理解这个公式,没有理解它的实质,更没有上升到对勾股定理三边关系高度概括化的认识。其实,没有总结提升和内化,学生即使练习再多的勾股定理题目,同样会出现这样的错误,甚至会强化这样的错误。
4.情绪化现象普遍,降低了学习数学的温度
进入八年级后,一部分学生对数学知识的学习方法和认识还是停留在七年级的水平,特别是对逻辑性较强的推理和证明不知所措,很难理解老师所讲的问题。这会导致学生的挫折感和失败感;再加上心理调节能力有限,有时又缺少外界及时合理的开导和鼓励,学生会觉得学习数学特别费劲,甚至失去信心,滋生厌学情绪。
5.创新性思维匮乏,遏制了学习数学的热度
数学教学不仅训练学生严谨的思维过程,也不断促进学生思维的创新。学生只有听懂了,感兴趣了,才能更好地去理解数学内容,数学思维的活跃程度才能高,也才可能有课堂的创新。然而,纵观我们的数学课堂,沉闷、无味、一讲到底的情况依然存在,有时甚至是常态。这样的数学课堂,很难引起处于青春期的八年级学生的兴趣,更谈不上帮助学生很好地理解其教学内容,提升数学理解力。
二、初中生数学理解力弱化的教学修正
提高数学理解力,就要从学生的实际出发,以学生已有的知识结构为依据构建知识体系,系统地培养学生的阅读、创新等能力。笔者在教学实践中尝试了以下几种教学策略,收到了一定的效果。
1.加强知识点勾连,形成数学知识链条
苏科版教材对于初中三个年级的数学内容安排的层次非常清晰,其结构层层递进,但八年级与七年级的知识点存在明显断层,加之八年级学生思维发展存在瓶颈,这就给学生学习带来了很大的困难。这时候就需要我们教师引导学生加强知识点的勾连,等一等,缓一缓,想一想,分层递进,分步解决。比如,在教学《等腰三角形的性质和判定》这一课时,从知识本身来看,学生可以利用轴对称性发现等腰三角形的相关性质;从证明过程来看,学生已初步掌握有条理地思考与表达;从活动经验来看,学生已初步体验到观察、操作、实验、猜想得到的结论有时是不全面的、不深入的,甚至是错误的,明白证明的必要性。但这些感受还是较肤浅的,并且学生演绎推理的能力还比较薄弱,思维的广阔性、严密性、灵活性比较欠缺。因此,要从学生原有的认知基础出发,以学生自主探索、合作交流为主要方式,让学生经历等腰三角形性质的形成与应用的过程。具体来说,一是要通过创设具有启发性的、学生感兴趣的、有助自主学习和探索的问题情境,使学生在积极思维的状态中进行主动探究,发现证明等腰三角形的性质和判定定理的证明思路,明确“怎么想”与“怎么写”之间的关系;二是通过此探索活动进一步理解合情推理和演绎推理都是获得数学结论的重要途径,体会证明的必要性,发展学生合乎逻辑的思考和有条理的表达能力;三是对互逆命题的真假判断和例题的拓展,和学生一起探讨辨别命题真假的方法;四是通过积累活动经验,进一步理解“观察—猜想—概括—论证”这一数学发现的过程,同时为后续的有关三角形、四边形中相关定理的证明提供经验储备和证明依据。比如,在讨论思考与表达之间的关系时,为了加深学生的理解,我们可以分步骤进行(见图1):
规范正确的证明书写格式,即怎样将头脑想的思路转化成数学语言,是困扰许多学生的一个问题。在学生讨论交流的基础上,教师添加“箭头”,重现“小黑板”,点明“怎么想”是我们证明的思路,是从结论入手的,而写出它的证明过程要从已知条件入手,也就是将“怎么想“的过程逆过来,二者是互逆关系。分步骤层层递进,推进学生理解数学、理解数学课堂,这样学生才能抓住我们的数学课堂,也能更好地学好数学,提升学生学习数学的兴趣,增强数学理解力。
2.注重阅读力培养,提高数学审题能力
数学不仅是一门学科,还是一种描述自然科学的语言。美国心理学家布龙菲尔德说过,“数学不过是语言所能达到的最高境界”。数学本身就需要阅读,但有别于语文阅读。数学语言具有高度的抽象性、严谨性和精确性,尤其是一些符号语言、图形语言。因此在平时的数学课堂教学中,要注重学生阅读能力的培养,让学生养成认真细致、勤思多想的习惯,认真读题,真正读懂题,逐步提升审题能力。
例如,在一次数学测试中有这样一道改编题:
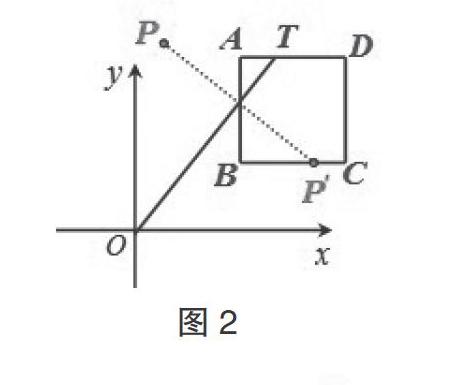
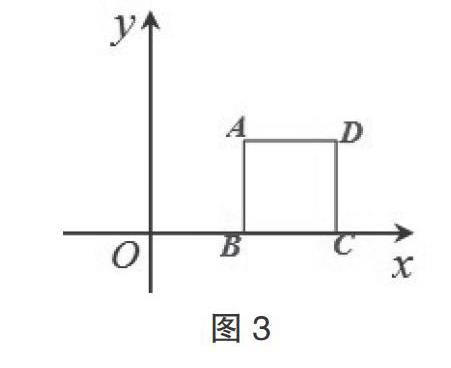
在平面直角坐标系中,对于点P和正方形ABCD,给出如下定义:若正方形ABCD上存在一点T不与O重合,使点P关于直线OT的对称点也在正方形ABCD上,则称P为正方形ABCD的反射点。下图2为正方形ABCD的反射点P的示意图。
(1)如图3,已知点B的坐标为(2,0),正方形ABCD的边长为2。
①在点E(0, 5),M(1, 2),N(0, -3)中,正方形ABCD的反射点是____________。
②点P在直线y=x上,若P为正方形ABCD的反射点,求点P的横坐标的取值范围。
(2)如图4,平移图3中的正方形ABCD,使它的中心Q在x轴上,若轴上存在点P是正方形ABCD的反射点,直接写出正方形ABCD中心Q的横坐标x的取值范围。
本题的得分率非常低,平时数学学得不错的學生仅能判断出第一问中三个点是否是反射点,而且是花了较长时间去画图,有的是猜对了,自己也说不清为什么。其实,这很大一部分原因是没有读懂题意,或是没有充分抓住题目的本质。在讲解该题时,我设计了几个小步骤:①P和P'对称说明什么?②O到正方形最近的距离是多少?③O到正方形最远的距离是多少?这样便于学生理解反射点的本质:首先,由对称可知,OP=OP',所以P点不能太远也不能太近,OP的长度范围很显然受到O到正方形的距离影响;其次,还要保证∠POP'的角平分线能穿过正方形,才能符合反射点的特点。通过这样的分析,引导学生在阅读数学题时要学会通过对于已知问题的转化来抓住问题的本质,才能深入理解移动变化后的反射点的情况。学生通过分析后很快理解在解答第二问时需要考虑长度和角度,对于最后一问,学生通过分析也顺利地找到最远的一种情况,问题就迎刃而解了。对问题这样的分析和引导使学生不仅从知识层面加深了理解,从方法提升角度也有较大的收获。
3.提升逻辑思维水平,提炼数学思想方法
问题是数学的心脏,思想是数学的灵魂,方法是数学的行为。数学教学的核心是数学思想方法的培养和建立。解决数学问题的过程既是应用数学知识和数学思想方法的过程,也是学生进一步巩固数学知识,培养解决问题能力的过程[3]。因此,在数学教学中,不仅要重视知识形成过程,还要重视挖掘在数学知识的发生、形成和发展过程中所蕴藏的数学思想方法。
首先,要深入挖掘隐含在教材里的数学思想方法。教师应精心设计课堂教学过程,展示数学思维过程,让学生了解不同数学思想方法的产生、应用和发展的过程,理解数学思想方法的特征、应用的条件,掌握数学思想方法的实质。例如,立体几何教学中许多内容都体现了一个重要的思想方法,就是把空间里的问题转化为平面上的问题。在教学过程中,教师要引导学生从具体问题中提炼出这一具有普遍指导作用的思想方法,并进一步上升为降维的思想方法,再总结出更高层次的思想转化与化归。
其次,要有意识地运用数学思想方法。对于数学重难点的教学,教师要有意识地运用或揭示数学思想方法。数学教学中的难点,往往与数学思想方法的综合运用有关。因此,教师要掌握重点,突破难点,更要有意识地运用数学思想方法组织教学。例如,二次根式的加减运算是一个教学难点,为了突破难点,就要运用类比思想、整体思想、化归转换思想等方法寻找解决问题的途径,采用类比整式的加减运算的手段,构造出具体形象的数学模型,从而进行猜想、推理、研究,实现从未知到已知的转化。
再次,要通过范例教学挖掘数学思想方法。有意识地组织学生进行必要的解题训练,设计具有探索性的、能从中抽象出一般和特殊规律的范例进行教学,在对其分析和思考的过程中展示数学思想和具有代表性的数学方法。教师应对数学思维活动过程中展示出来的数学思想方法及时地进行提问与讨论,启发、引导学生领悟出思想方法。比如,在教学一次函数时,可从函数本身的定义出发,研究它的解析式、图像、性质,这种过程显然是符合知识的发生发展规律的。老师应及时总结并引导学生去探究这个过程。学生在充分理解的基础上来学习函数,也就较容易触摸到知识的本质,为后面反比例函数、二次函数的学习提供极好的模板和参照。
数学思想和方法不是学生通过几个题目的练习就能总结出来并随时使用的。八年级的学生没有接触太多的数学思想方法,解题思路不清,逻辑混乱,但是他们已经有了零散的知识积累。在教学过程中,老师应有意识地渗透数学思想方法,引导学生按照一定的知识序列有条理地将知识点串联起来,让他们有计划地、有步骤地进行总结反思,逐步提升逻辑思维水平,最终提炼出数学思想方法。
4.关注情绪化体验,树立数学学习自信
八年级学生在数学学习上出现分化现象,部分学生对学习数学渐渐失去信心。究其原因,除了认知结构跳跃大外,情绪波动大、心理自我调节弱也是很重要的原因。俗话说,“亲其师,信其道”,教师要注重与学生交流,建立和谐的师生关系,才能转变学生的学习态度,激发他们学习的主动性。
对于有自卑情绪的学生,在课堂教学中,我们加强小组合作学习,创设良好的学习氛围,注重学生的资源开发,列举学生感兴趣的事例,激发学习兴趣,帮助他们树立学好数学的自信心,从而提高学生对数学课的专注度。
对于有畏难情绪的学生,在课堂教学中,我们采取分层教学的方式,适当减低学习难度,让学生体会到学习数学的乐趣,增强学习自信,从而想学、会学。当学生数学成绩提高了,我们要及时给予鼓励,这种鼓励既要有仪式感,也要有成就感。例如,部分数学作业批改采用批语的形式,坚持使用“书写规范,过程完整,如能再细心一点就更好了,相信你能做到!”“再思考思考,能完善一下解答过程吗?”“解法巧妙,还有更好的方法吗?”等批语进行师生对话,既及时纠正了学生作业中存在的问题,又增进了师生之间的感情,树立了学生学好数学的信心。
5.创新教学手段,提升数学学习效能
创新是进步和发展的强大动力,初中数学教学模式的固化导致教学效率的下降和学生学习积极性的受挫。因此,在新课程改革不断实施的过程中,初中数学教师应该不断创新教学手段,丰富教学形式,以创新的形式来激发学生课堂学习兴趣,从而提升学习效能。此外,教学要留白,即留给学生自我消化的时间,把刚刚讲过的不懂的知识点及时再自我消化理解,以便切实掌握。
在数学课堂教学中,我们利用《伴你学》中的问题导学部分内容,结合老师的教学经验,安排学生的自主预习。对于在自主预习过程中发现的不懂的问题或是不理解的内容,小组交流讨论,经过小组讨论依然解决不了的,再通过小组汇报的形式呈现到课堂上,由全班同学和老师来共同完成。学生经历充分的思考和交流,展示了自己的思维过程,更细致地理解了知识的形成和思维的发展过程。教师能了解学生的思维及存在的问题,及时调整教学设计。在此基础上,教师再给出具有层次性和跳越性的问题,抓住学生的注意力和兴趣点,引导他们进行交流、讨论、合作探究,促进知识的掌握和能力的形成。教师设计安排互动方式要合理,内容要贴近主题,问题要抓住学生思维的漏洞和错误,让他们自己感知,经历问题—思考—交流—解決的过程,使课堂教学得到进一步的优化。
此外,我们还针对不同课型,不同班级和不同层次的学生,采取灵活有效的方式进行教学,不拘泥于模式,重点关注学生的“动”,关注“教与学”的高效,注重对数学思维方式和方法的训练和指导,让学生知道数学问题应该从什么角度,按什么方法进行思考,从而突破了八年级数学学习的瓶颈,提升了数学思维力和创新能力。
总之,在数学教学过程中,根据八年级学生身心变化特点,首先,教师要科学设计有价值的学习内容,调控学习过程,以学生为主体,以问题为主线,促使学生真学;其次,教师的引导要符合知识本身内在的逻辑序列和背后的思想方法,将学生的思维引向更高层次,促使学生深学;再次,教师要关注学生的情感体验,根据学生的学习状态组织、实施和调整教学,充分调动学生的主动性,促使学生乐学。这样,就可以让八年级学生的数学理解力得以实实在在地提升。
参考文献:
[1]曲永华.“八年级现象”的探究及应对措施[J].辽宁教育, 2017(16):45-47.
[2]周莹.高中生数学教材阅读策略研究[D].宁波:宁波大学, 2017:2-5.
[3]周淑红.小学数学核心素养培养研究[D].哈尔滨:哈尔滨师范大学, 2017:2-4.
责任编辑:赵赟
Realistic Interpretation and Teaching Rectification of Junior Middle School Students Weaker Ability of Comprehending Mathematics
ZHANG Zhaoju
(Lianyungang Foreign Languages School, Lianyungang 222006, China)
Abstract: For reasons of discontinued knowledge points in the teaching materials of junior middle school Grade-Eight mathematics, more difficult contents, students lack of reading transforming ability, non-rigorous logical thinking, weak ability of mental adjustment, and shortage of creative thinking, students ability of comprehending mathematics is getting increasingly weaker. To solve the problems, teachers should pay attention to the following points: strengthening connection of knowledge points to form the chains of knowledge, emphasizing cultivation of reading ability to improve their ability of mathematical examination, enhancing the level of logical thinking to refine mathematical thinking methods, focusing on emotional experience to build their confidence in mathematics learning, and creating teaching means to promote the efficiency of mathematics learning.
Key words: ability of comprehension; mathematics reading; mathematics knowledge; teaching rectification
