MetaCCA在多元表型与基因型相关分析中的应用

贾晓灿，杨永利，王 威，施学忠

1)郑州大学公共卫生学院卫生统计学教研室 郑州 450001 2)郑州大学公共卫生学院劳动卫生与职业病学教研室 郑州 450001

过去十几年，全基因组关联分析(genome-wide association study, GWAS)在识别疾病的常见变异方面取得了巨大进展，但越来越多的研究[1-2]结果表明罕见变异在复杂疾病的发生发展中同样起着很大作用。单位点分析的GWAS忽略了不同表型之间的相关信息，因此不能有效识别复杂疾病中的罕见变异。MetaCCA也称Summary statistics-based multivariate meta-analysis of genome-wide association studies using canonical correlation analysis[3]，是利用典型相关分析(canonical correlation analysis, CCA)的原理，对GWAS的汇总统计结果进行分析，以探讨多个疾病表型与基因型之间的关系，从而为研究疾病的发病机制提供依据[3-6]。该文将重点介绍metaCCA的原理和实现，并探讨其在多元表型与基因型相关分析中的应用前景。

1 MetaCCA简介

1.1MetaCCA的提出2005年Klein等[7]在Science杂志上首次报道了视网膜黄色雀斑的GWAS结果，并发现一个与视网膜黄色雀斑有显著关联的基因。此后，一系列针对人类复杂疾病或性状的GWAS相继开展，在肥胖、高血压、高血脂、心血管系统疾病、肿瘤、神经精神类疾病等诸多疾病方面取得了突飞猛进的研究成果[8-10]。GWAS逐渐成为识别疾病遗传变异最常用的方法，为众多疾病的基因诊断及个体化治疗提供了理论基础。

GWAS是一种单因素分析方法，它只能分析一个单核苷酸多态性(single-nucleotide polymorphism，SNP)与一个表型之间的关系，忽略了多个SNP之间的内部关联性以及复杂疾病中多个表型之间的相关性，因此检验效能有限[11-12]。随着海量测序数据、基因表达数据、多维数据以及多元表型复杂疾病的出现，GWAS的局限性也越来越凸显。此外，GWAS分析的数据需要具体到个体水平上，由于个体水平上的测序成本高而且数据需保密，因此目前仅有部分GWAS的汇总结果得以公开。如何基于公开发表的GWAS汇总统计的数据库识别复杂疾病中的罕见变异，已成为目前基因组学研究面临的主要问题[13]。2015年，Cichonska等[3]首次在《Bioinformatics》杂志上提出metaCCA的方法。CCA是一种分别提取自变量集与因变量集的最大主成分，通过两个主成分的相关关系推测自变量集与因变量集之间的相关关系的方法[14]。MetaCCA是对公开发表的GWAS的汇总结果进行整理，利用传统统计方法CCA，检测多个SNP与多个疾病表型之间的关系。

1.2MetaCCA的优点与传统的GWAS相比，metaCCA有如下优点。首先，metaCCA将多个GWAS结果汇总在一起，增大了样本量，提高了检验效能。其次，metaCCA利用的是已公开发表的GWSA数据，不需要个体水平上的测序，是一个成本-效益较高的方法。最后，metaCCA借助于CCA的原理，既考虑到了基因型之间的内部关联性，又考虑到了疾病表型之间的相关性。而传统的检验多元表型与基因型相关性的方法是逐个对表型单之间与基因关联性进行检验，然后采用多重检验校正。然而同一疾病的多元表型之间往往具有相关性，基于单个表型与基因型的关联性分析难以全面揭示遗传与复杂疾病的联系[15]。利用多元表型变量间的相关性，从多元表型变量中提取类似主成分因子的策略进行相关分析，是识别复杂疾病中罕见变异的有效方法[16]。

2 模型建立与实现

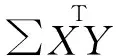
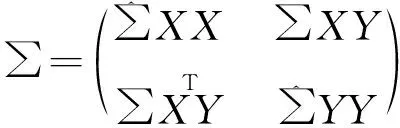
①∑XY由单个SNP与单个表型变量的回归系数β的矩阵组成，β可由单变量GWAS的汇总统计结果获得，其表达式为:

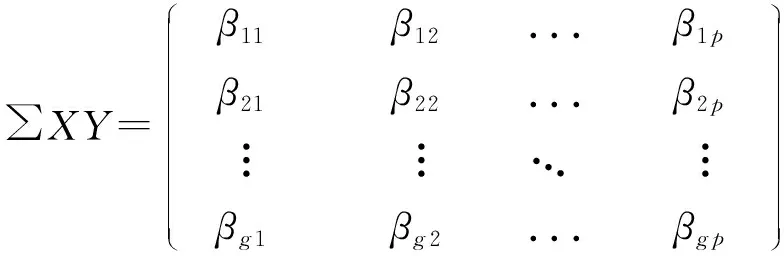
式(2)中，g为基因型变量个数，一般为SNP个数；p为表型变量个数。

需要注意的是，X和Y应标准化转换后才可以带入计算，其标准化公式为：

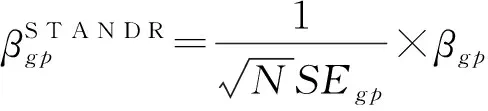
式(3)中，N为样本量，SEgp为βgp的标准误，也可以由单变量的GWAS汇总统计结果获得。

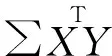
经过以上步骤可得出总协方差矩阵，在将此协方差导入CCA模型之前，需要先判断总协方差矩阵是否为半正定矩阵(positive semidefinite，PSD)。当不满足PSD时，需要使用迭代方法对矩阵进行降维，直至满足PSD。此后，将总协方差矩阵进行CCA，计算基因型与表型之间的典型相关系数r：

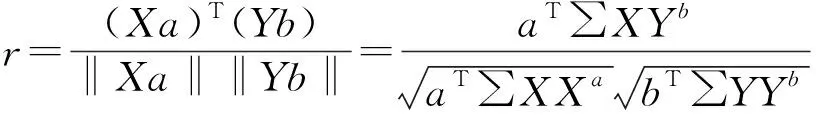
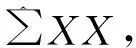
2.3软件实现及程序包MetaCCA主要通过Plink软件(http://zzz.bwh.harvard.edu/plink/download.shtml)及R中的metaCCA包(https://github.com/MoisesExpositoAlonso/metaCCA)实现。假设将原始GWAS汇总统计结果整理后得到一个样本量为n、含1 000个SNP和10个性状的数据集S_XY_full_study，则metaCCA的软件实现过程如下：

plink2 --file hapmap3 --extract SNP_id --keep CEU_hapmap --r2 inter-chr with-freqs --ld-window-r2 0 --make-bed --out uppro

S_YY=estimateSyy(S_XY=S_XY_full_study)

输出结果为10×10的相关系数矩阵。

③利用metaCCA包中的metaCcaGp函数进行单个SNP(以rs123为例)与10个表型之间的相关分析，输入数据为S_XY_full_study,代码为：

result=metaCcaGp( nr_studies=1),

S_XY=list(S_XY_full_study),

std_info=0,

S_YY=list(estimateSyy(S_XY_full_study)),

N=n,

analysis_type=1,

SNP_id=(′rs123′)

输出结果有三列，分别为“rs123”“典型相关系数r”和“-Log10P”

④假设rs123、rs125和rs127分布在基因A上，利用metaCCA包中的metaCcaGp函数进行基因A与10个表型之间的相关分析。输入数据为S_XX_study和S_XY_full_study,代码为：

result=metaCcaGp(nr_studies=1),

S_XY=list(S_XY_full_study),

std_info=0,

S_YY=list(estimateSyy(S_XY_full_study)),

N=n,

analysis_type=2,

SNP_id=c(′rs123′,′125′,′rs127′),

S_XX=list(S_XX_study)

输出结果有3列，分别为“rs123、rs125和rs127”(即基因A)、“典型相关系数r”和“-Log10P”。

3 MetaCCA在医学中的应用

3.1血脂水平相关基因的识别Cichonska等[3]利用3个芬兰人群9个血脂表型的数据进行了metaCCA分析并与个体水平上的GWAS和CCA结果进行对比，纳入的SNP有455 521个。与单变量GWAS结果相比，metaCCA的检验效能较高。比如GWAS结果显示USP1/DOCK7和FCGR2A/3A/2C/3B两个区域的SNP与血脂水平相关(P<5×10-8)；通过metaCCA进一步验证了此结果，而且发现了位于PCSK9/BSND、CELSR2和GALNT2基因区域的位点。基因水平上的分析选择了5个基因，包括APOE、CETP、GCKR、PCSK9和NOD2，其中APOE、CETP、GCKR和 PCSK9已经被之前的研究证实和血脂水平相关，而NOD2未见报道。与个体水平上的CCA相比，metaCCA的结果比较准确，所选择的5个基因中，有4个基因结果的绝对误差不超过0.2。

3.2精神疾病共有风险基因的识别精神疾病是一类以感知和认知障碍导致行为、意志和情绪异常的复杂疾病。常见的精神疾病有精神分裂症、双相情感障碍、抑郁症、孤独症和注意缺陷多动症[18]。从血液样品中抽提出患者全基因组DNA，使用群体遗传学知识和统计推断技术寻找与疾病相关的遗传变异，是研究复杂精神疾病遗传变异的主要途径[19]。已有的GWAS和生物通路分析均显示这几种常见精神疾病之间存在共有的遗传风险位点和生物路径[20-21]。本课题组[22-23]利用metaCCA对美国精神病学基因组学联盟(Psychiatric Genomics Consortium，PGC，网址: http://www.med.unc.edu/pgc/)的数据进行了统计分析，共发现37个多态性基因，其中13个已被报道与多种精神疾病相关，4个被报道仅与一种精神疾病相关，另有20个为新发现的基因。此外，基因功能富集分析结果显示，这37个基因与黄素腺嘌呤二核苷酸结合、电压门控钙通路等多个路径相关。这些被发现的基因为精神疾病的发病机制研究提供了线索。

4 MetaCCA的局限和挑战

MetaCCA在多元表型与基因型数据关联分析方面的应用，很大程度上增强了人们对复杂疾病遗传机制的理解，对于复杂疾病的预防、治疗有较大的实际意义，但是，也存在一定的局限性。首先，metaCCA主要依赖统计分析，因此可能会出现假阳性结果，尤其是在基因和通路水平上，容易出现某个SNP和多个表型强相关而导致该SNP所在的基因或通路有意义，此时就需要其他基因水平的统计方法或多元统计方法对metaCCA的结果进行筛选，或者结合基因功能分析结果综合下结论。其次，metaCCA需要将多个GWAS结果整合在一起，而原有的GWAS选取的参照数据库模板、最小等位基因频率等处理因素可能不同，在数据筛选过程中，需控制或降低这些混杂因素的影响以及避免几个研究之间样本的重复。再次，metaCCA的核心思想是CCA，而CCA在纳入变量时需要对原始变量进行筛选，当同一组内的变量存在较强相关关系时，一般建议删除其中一个变量或将变量合并，以得到更加合理的模型。因此，对于metaCCA纳入的基因型变量应通过连锁不平衡或线性模型等方法进行筛选；对于表型变量，不仅要考虑临床症状的相似性、生物路径的相同性，还要考虑各变量之间相关性的强弱。最后，metaCCA的结果只能表明基因型与表型之间有无统计学关联，其生物学机制还需实验研究来证实。

5 小结

目前，对于metaCCA的研究虽处于起步阶段，但已经为人类复杂性遗传疾病以及高维数据的研究打开了一扇大门。该方法具有高通量、低成本、不涉及候选基因等优点，是目前分析多元表型与基因型相关关系的有效途径，也可应用于基因组学、蛋白质组学等方面的研究，从而为人类了解复杂性疾病的发病机制提供更多的线索，但其理论和方法还需在应用中进一步完善。