房价影响因素的研究及预测—以阜阳市为例

（阜阳师范学院数学与统计学院，安徽 阜阳236037）

1 引言

近年来，房价问题一直受到社会各界的广泛关注,房价的高低也影响到社会诸多方面的利益。与此同时，房价的影响因素和房价的预测问题也倍受社会各界人士的关注。其中，房价的预测不仅可以为投资决策和消费决策提供参考,也可以为政府相关部门的行政决策提供参考，具有颇高的现实价值。

本文在大量统计数据基础上，建立相应的数学模型，对阜阳市房价的影响因素进行研究并做出预测。首先，通过线性拟合的方法并借助Excel软件进行图像的绘制，找出影响阜阳市房价变化的因素。其次，建立主成分分析模型，利用MATLAB软件计算出各项指标在总指标中的贡献率及主成分的个数，找出影响阜阳房地产价格的主要因素及其影响程度，最终实现对阜阳市房价影响因素的研究。最后，建立多元回归模型，对房价进行预测。

2 问题的研究

2.1 房价影响因素的研究

为了找出阜阳市房价的影响因素，本文将采用线性拟合的方法对其进行研究。

通过调查，本文主要从以下几个指标来分析阜阳市房价的影响因素，具体如下表。

表1 房价影响指标体系表

将收集到的数据进行整理，然后利用EXCEL软件进行线性拟合得到如下图像：

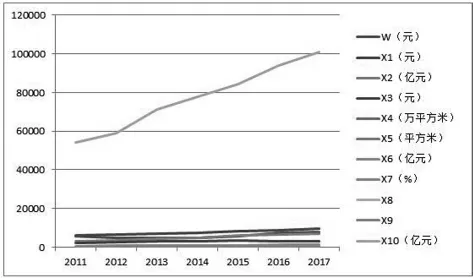
图1 2011-2017年各指标与房价变化趋势图

由图1可以看出，在2011年至2017年期间，由于通货膨胀的原因，导致人民币贬值，出现各年份的货币供应量偏差较大，无法较为准确的预测其未来几年的变化状况。因此，将X10这一指标舍去，最后将影响房价的指标确定为X1,X2，L，X9。

2.2 房价主要影响因素的研究

对于主要影响因素的研究，本文将采用主成分分析法[2]（PCA）对其进行研究。

2.2.1 主成分分析的概念及原理

主成分分析也称主分量分析（PCA），就是设法将原来众多的具有一定相关性的指标，重新组合成几个相互无关的综合指标，并且尽可能的反映原来指标所带有的一些信息，实现了维数的降低，从而简化问题便于分析。

为了使这种综合指标F1反映足够多原来的信息，则要求综合指标的方差要大，即Var（F1）越大，F1所包含的信息量越多，因此在所有线性组合中选取的F1应该是方差最大的，故称F1为第一主成分。如果第一组成分不足以代表原来P个指标的信息，再考虑选取第二个线性组合F2，其中F1中已有的信息就不需要出现在 F2中，即要求 Cov（F1，F2）＝0,称F2为第二主成分,以此类推即可构造出第三，第四，AA，第 P 个主成分[2]。

2.2.2 主成分分析法下的数学模型

对通过2.1筛选后的收集到的9项指标，X1，X2L，X2每个指标有7个观测数据，便得到原始数据资料矩阵

现用矩阵 X 的 9 个向量 X1，X2，L，X9，作线性组合，得到

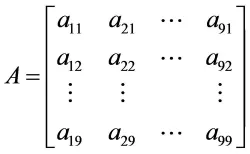
X=（X1，X2，L，X9），且系数 aij有下列原则决定：

①Fi与 Fj（i≠j）不相关；

主成分分析计算步骤[2]如下：

（一）对所收集到的关于房价的影响指标数据进行标准化，以消除各变量在单位上的相互影响；

（二）根据标准化后的矩阵求出相关系数矩阵R＝（rij）9×9.

（三）根据（二）中所求相关系数矩阵，进而可得到其对应的特征根 λi（i＝1，2，L，9）和对应的特征向量 ei（i＝1，2，L，9），其中 eij表示向量的第 j各分量；

（四）计算主成分的贡献率和累积贡献率

其中，主成分Zi的贡献率为

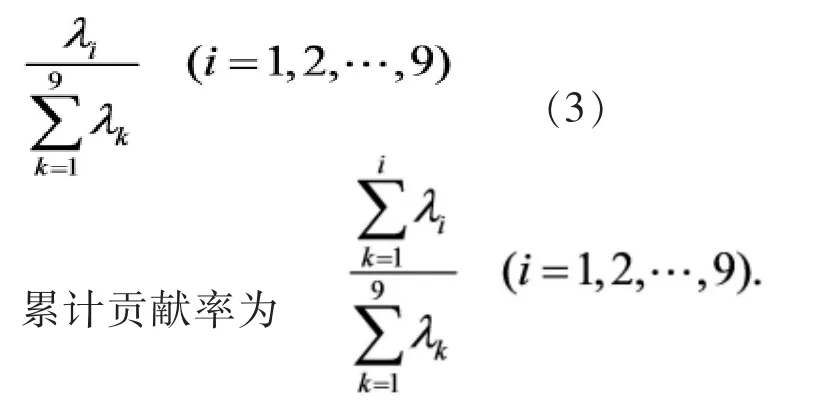
通过 MATLAB 软件计算可得 X1，X2，L，X9的贡献率分别为-0.0000、0.0000、 0.0000、 0.0015、0.0062、0.0181、0.0444、0.1499、0.7798。 由 MATLAB计算结果可知主成分数为2，且要保证累计贡献率达85%-95%，则易知最后两个指标的累计贡献率为92.97%，是主成分，说明主要成分X8，X9已经包含 X1，X2，L，X9这些指标所具有的信息。 从而，实现简化问题的目的。

（五）计算主成分的载荷数，计算公式为

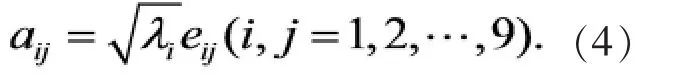
便可得到各主成分载荷矩阵

（六）然后对载荷矩阵进行单位化，得到A＝（aij）

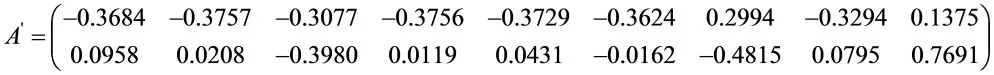
（七）阜阳市房价的第一、二主成分为

根据以上结果可知：

①在第一主成分的表达式中，我们可以看出第一、二、四、五、六项的系数比较大，这五项指标对房价的变化影响较大，其中X2阜阳市生产总值、X4新增保障性住房面积、X5人均住宅建筑面积的系数相较于另外两项大，说明阜阳市生产总值、新增保障性住房面积和人均住宅建筑面积在房价变化过程中占重要地位。

②在第二主成分的表达式中，我们可以看出只有第三项和第七项的系数相对来说较大，且远远超过其他指标的系数。因此，恩格尔系数和经济适用房销售价格对阜阳市房价变化的影响较大。

综上，我们可以得知对阜阳市房价影响最主要的因素有：城市化率和CPI.

2.3 房价的预测

通过2.2的研究，我们已经确定了影响阜阳市房价变化的主要因素。为了检验其正确性，本文将建立多元线性回归模型[2]，确定模型的参数代到回归方程进行检验。

2.3.1 多元线性回归的定义

一切运动着的事物之间总存在着一定的相互联系，其中这些运动的事物相当于变量。而回归分析就是处理变量之间相互关系的一种数理统计方法。线性回归即是变量之间的关系为线性关系，同时根据自变量的多少，将线性回归可分为一元线性回归和多元线性回归[2]。

2.3.2 多元线性回归模型的建立

设有 p+1 个变量，x1，x2，Λ，xp，y，β0，β1，β2，Λ，βp为未知参数，则变量间的关系可用如下式子进行表示

其中，ε 为随机误差且服从正态分布（0，σ2），叫做回归常数，叫做回归系数[2]。

现 x1，x2，Λ，xpy对分别进行 n次观测， 可得 n组样本，xi1，xi2，Λ，xi（P－1），yi，（i＝1，2，Λ，n）则有

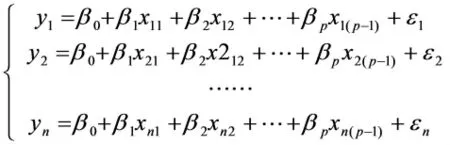
其中，ε1，ε2，Λ，εn相互独立且

εi：N（0，σ2）

现令

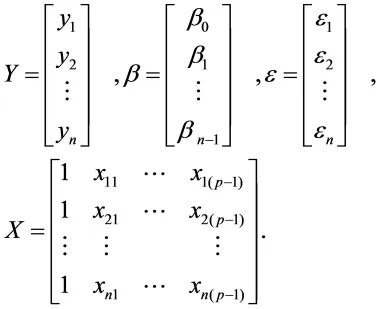
则上式可表示为

由于线性回归分析的主要任务是用样本值对β0，β1，β2，Λ，βp和 σ 作点估计； 对回归系数 β0，β1，β2，Λ，βp作假设性检验。现利用最小二乘法对β进行估计，即选择合适的β，使得误差项的平方和最小。

对于建立的数学模型，为了检验其拟合度、显著性将要对模型进行检验。检验的常用方法有F检验、t检验、R检验，下面就R检验为例进行叙述。

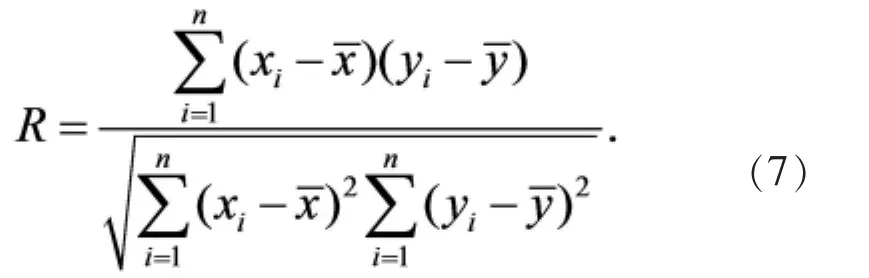
其中，R为线相关系数，用于判断回归模型的拟合的程度。 当 R 越大，y 与 x1，x2，L，xP的线性关系越显著。

2.3.3 根据回归分析得到房价与主要影响指标的关系模型

通过2.2的研究，我们得知阜阳市房价变化主要受城市化率和CPI的影响。为了使结果更为准确，本文先采用线性模型[7]，再采用二次模型[7]。

1、线性模型

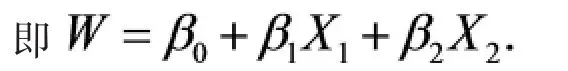
借助MATLAB软件可以得到rmse的值为1.5741，stats的值为 0.0000、0.0000、0.0000、155.33，bata 的值为-2.9353、2.2358、1.6910.

便可得回归方程为

2、纯二次模型

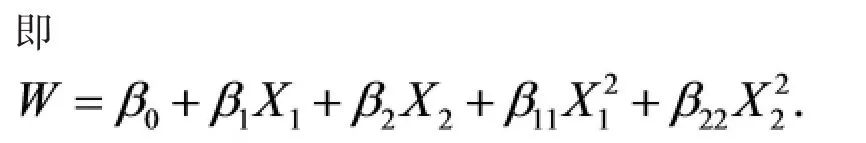
借助MATLAB软件可以得到rmse的值为1.5741，stats的值为 0.0000、0.0000、0.0000、2.4779，bata 的 值 为 -1.3461、-0.8222、3.3320、0.5126、 -1.6504.

便可得回归方程为

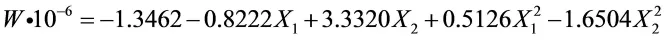
通过以上两种类型的回归模型的建立，可以较为准确的把握房价与城市化率和CPI的关系。同时，得到残差图和预测交互图如下：

图2 残差图

根据残差图可以看出，各数据的残差离零点均较近，且残差的置信区间均包含零点，这说明回归模型能够较好地符合原始数据。

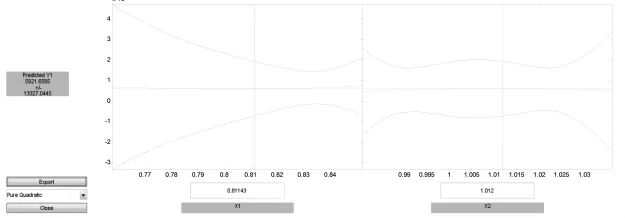
图3 预测交互图

根据预测交互图，在左边图片下方的方框中输入城市化率，右边图片下方的方框输入CPI，则在画面左边的“Pre-dicted Y1”下方的数据即为在该城市化率，CPI下的房价。

3 本文结论

经过本文的研究，我们得出影响阜阳市房价变动的主要因素为城市化率和CPI。同时，通过建立相关模型对阜阳市未来几年的房价展开了预测。最终发现阜阳市房价在近几年内依然会略有上涨，但变化幅度不大。这将解决广大购房者的购房困惑，即在城市化率和CPI变化幅度较小时购房最为恰当。同时，为投资决策、消费决策和政府的行政决策都有较高的指导意义和参考价值。

编辑：林军