向量法在立体几何中的应用

云南省开远市第四中学 董秋理

立体几何一直是高中数学的一个难点，解决这个难题的最好工具就是空间向量。向量融数、形于一体，具有代数形式和几何形式“双重身份”，具有线性运算、数量积，既有有向线段表达式，又有坐标表达式，是解决立体几何问题的一种重要工具，向量本身的这些特点决定了它与立体几何、解析几何、三角函数等内容的自然融合，是知识的“交汇点”。

一、平面法向量的坐标的求法

一般根据平面法向量的定义推导出平面的法向量，推导平面法向量的方法如下：

例1，在例1的条件下，求平面ACD1的法向量和平面A1ABB1的法向量

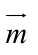
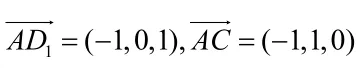
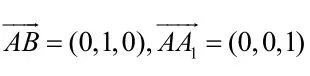
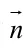
二、空间向量在求解立体几何题中的应用举例

（一）空间向量在求空间距离中的应用

1.点到平面的距离、直线与平面的距离、平面与平面的距离

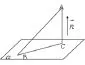
直线与平面的距离、平面与平面的距离均

可以转化为点到平面的距离求解。当求直线与

平面的距离时，A，B 两点分别表示直线上的任意一点和平面上的任意一点，表示平面的法向量。

2.求异面直线间的距离

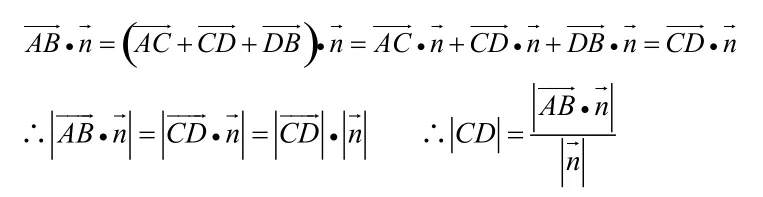
（二）空间向量在证明垂直、平行中的应用

要证明两直线垂直，只需证明这两条直线所对应的方向向量的数量积为；要证明直线垂直平面，只需证明这条直线所对应的方向向量与平面内不共线的两向量的数量积均为；要证明两平面垂直，只需证明一个平面内的一个向量垂直另一平面，或者证明两个平面的法向量的数量积为0。

要证明直线与平面平行，只需证明这条直线所对应的方向向量平行平面内的一个向量，或者证明这条直线所对应的方向向量垂直于平面的一个法向量；要证明平面与平面平行，只需证明这两个平面所对应的法向量平行，或者证明一个平面的法向量垂直另一个平面。

（三）空间向量在求空间角中的应用

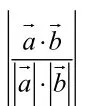
2.求直线与平面所成的角

设AB是平面α 的斜线，AC是平面α 的垂线，

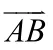
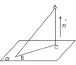
3.求二面角

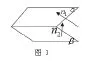
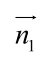
向量法的思维过程较简洁，规律性较强，解答比较容易，但需要正确建立空间直角坐标系及正确确定点的坐标。