平移齐次化妙解定点定值问题

广东省英德中学 陈国宗 全红盈

一、概述

圆锥曲线是历年高考命题的重点与难点，而定点定值问题又始终在圆锥曲线的问题中占有一席之地，该问题对学生分析问题能力，知识综合运用能力，数学运算能力与技巧要求较高.学生普遍存在计算不完或者计算不对的现象.为此，本文将介绍平移齐次化方法解决一类定点定值问题，以提高运算的效率与准确率.

二、例题分析

例1，已知A，B为抛物线x2=4y上异于原点O的两点，设kOA，kOB分别为直线OA，OB的斜率且kOA+kOB=2.证明：直线AB的斜率为定值.

解：设直线AB与抛物线的交点A(x1，y1)，B(x2，y2)，

设直线AB的方程为mx+ny=1.

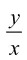
（1）求椭圆C的标准方程；

（2）证明：直线AB的斜率为定值.

解得a2=8或a2=3（舍去）

∴b2=a2-c2=2

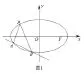
（2）分别平移x，y轴，建立以P(-2，1)为原点的直角坐标系x′Py′，如图2所示

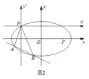
在直角坐标系x′Py′下：已知P(0，0)，设A(x1′，y1′ )，B(x2′ ，y2′)

设直线AB方程为mx′ +ny′=1

变形得：x′2+ 4y′2- 4x′+ 8y′=0

联立得：x′2+4y′2-4x′(mx′+ny′ )+ 8y′(mx′+ny′)=0

∵直线PA与直线PB的倾斜角互补，故kPA+kPB=0

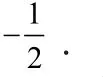
二是一般地，设P(x0，y0) (x0≠0)为圆锥曲线C:f(x，y) = 0上一点，由点P引倾斜角互补的两弦PA，PB，利用平移齐次化方法证明直线AB斜率为定值的基本步骤为：

①平移坐标轴，建立以P(x0，y0) (x0≠0)为原点的新平面直角坐标系x′Py′.

②在直角坐标系x′Py′下，求得圆锥曲线C的方程为f(x′+x0，y′+y0)=0，并将直线AB方程设为mx′ +ny′=1.

三是解题过程中应注意到圆锥曲线：C:f(x′+x0，y′+y0)=0的常数项为0，以及直线平移前后斜率不变的一般规律.

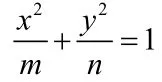
三、结束语

以上是本人对平移齐次化方法在定点定值问题中的一些见解，通过文中的几则实例，我们可以感受到该方法摒弃常规、独辟蹊径、解法高效.这也启发我们学习数学应该要有敢于创新、勇于突破的精神，而非墨守成规、千篇一律.