大型轴流转桨式水轮机桨叶操作机构有限元联合分析

任尚洁，刘思靓

(浙江富春江水电设备有限公司，杭州 311121)

0 引言

轴流转桨式水轮机的转轮叶片和导叶能随着工况变化形成最优的协联关系，从而提高水轮机平均效率，扩大运行范围，获得稳定特性[1]。

转轮桨叶操作机构连接着水轮机叶片，传递活塞的操作力，是实现桨叶角度变化的重要装置，包含活塞、操作架、耳柄螺栓、连板以及枢轴和拐臂等一系列部件[2]。

为保证机组的安全运行，要对操作机构设计方案进行计算分析，通常做法是单独对操作机构的某零件进行计算，但该做法忽略了机构零件间的协调变形，得到的应力会大于实际应力。在该结果的指导下，设计安全裕量会过大，对大型机组而言，会极大提高材料成本。

本文采用通用有限元分析软件ANSYS对某轴流转桨式水轮机组的桨叶操作机构进行整体联合计算。该机组装机容量高于200 MW，转轮直径大于10 m，是目前国内装机容量最大的轴流转桨式水轮机组。对桨叶操作机构进行整体分析，能更准确地得到各部件的应力分布和位移情况，在确保结构安全的前提下，更好地指导设计，控制成本。

1 联合分析的计算原理

使用有限单元法进行结构应力计算的基本思路是：对结构进行单元离散后，选择适当的位移函数来表达各离散单元节点的位移。

{f}=[N]{δ}e，

式中：{f}为单元内任一点的位移列阵；{δ}e为单元的节点位移列阵；[N]为形函数矩阵，表征位置坐标。

接着利用几何方程得到单元内任一点应变{ε}

{ε}=[B]{δ}e，

式中：[B]为单元应变矩阵。

然后，利用本构方程得到单元内任一点的应力列阵{σ}

{σ}=[D][B]{δ}e，

式中：[D]为应力-应变矩阵。

再利用变分原理建立单元节点力和节点位移的关系式，即可得到每个离散单元的平衡方程

{F}e=[k]e{δ}e，

式中：{F}e为单元的等效节点力列阵；[k]e为单元刚度矩阵。

最后，集合所有离散单元，建立整个结构的平衡方程

{F}=[k]{δ} 。

代入结构的刚度、载荷及边界，求解以上方程可得结构的节点位移列阵{δ}，再利用本构方程即可求得每个节点应力。

因此，利用有限元法求解应力分布的关键，是准确地得到结构各位置的位移[3-4]。

2 结构简介

桨叶操作机构靠活塞驱动，活塞杆带动操作架上下移动，操作架上的耳柄螺栓通过连杆带动拐臂转动，进而通过与拐臂把合的枢轴实现叶片角度的调节。转轮轮毂及其中的桨叶操作机构基本结构如图1所示。

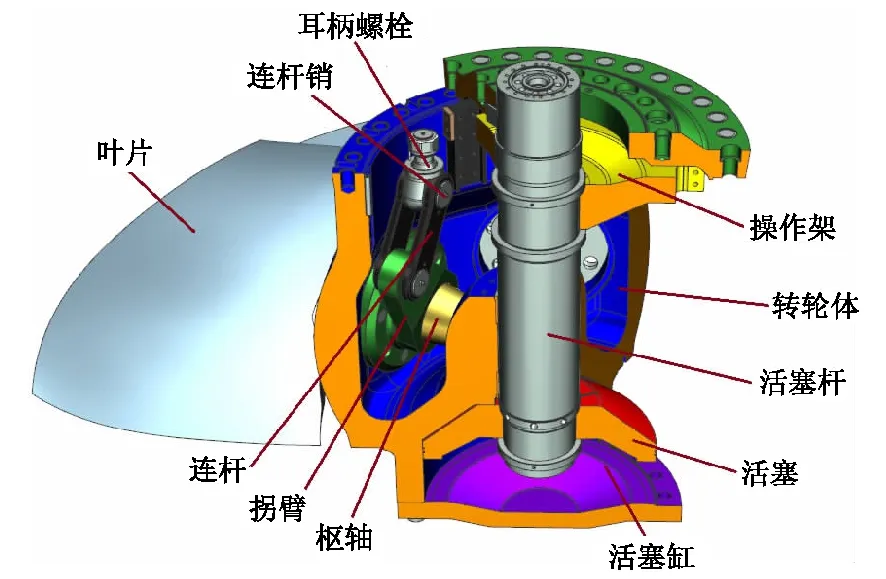
图1 桨叶操作机构基本结构Fig.1 Basic structure of the blade operating mechanism

3 整体联合分析

3.1 有限元模型

建立操作机构联合模型，并对其进行合理简化，忽略小销孔等细节。选用带中节点的实体单元建立操作机构的整体三维有限元网格模型[5]。根据结构的对称性，建立1/5模型，共计2 553 080个单元， 5 143 366个节点。模型包含操作架、耳柄螺栓、连杆、连杆销、拐臂和枢轴，转轮轮毂作为边界条件的一部分也包含在内。操作机构计算模型如图2所示。

图2 桨叶操作机构计算模型Fig.2 Calculation model of blade operating mechanism

计算桨叶全关且还具有关闭趋势时，即活塞杆运动趋势向上时各部件的刚强度。

各部件之间设置摩擦接触，剖切面设置循环对称。约束相应位置的平动或转动，施加叶片离心力和活塞杆传递操作力。耳柄螺栓预紧应力为250 MPa，操作机构加载如图3所示。

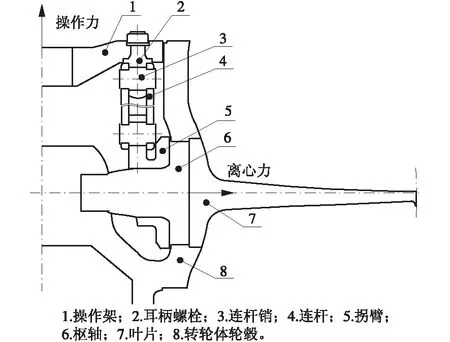
图3 桨叶操作机构加载示意Fig.3 Loading schematic of blade operating mechanism

3.2 联合计算结果

对该大型轴流转桨式水轮机组的桨叶操作机构进行联合分析，其整体应力分布如图4所示。

特别关注连杆和拐臂，其计算结果如图5～图8所示：连杆最大位移在耳柄端，为3.94 mm，最大拉伸变形为2.82 mm；连杆销孔内应力集中处的最大应力为526.0 MPa，连杆中间应力为45.7 MPa；拐臂最大位移在拐臂端部，为1.60 mm，不仅有转动位移约1.29 mm，还有转轮径向方向的位移；除叶片把合销孔内的应力奇异外，拐臂过渡倒圆应力集中处的最大应力为165.0 MPa，拐臂的连杆销孔应力集中处的最大应力为191.3 MPa。

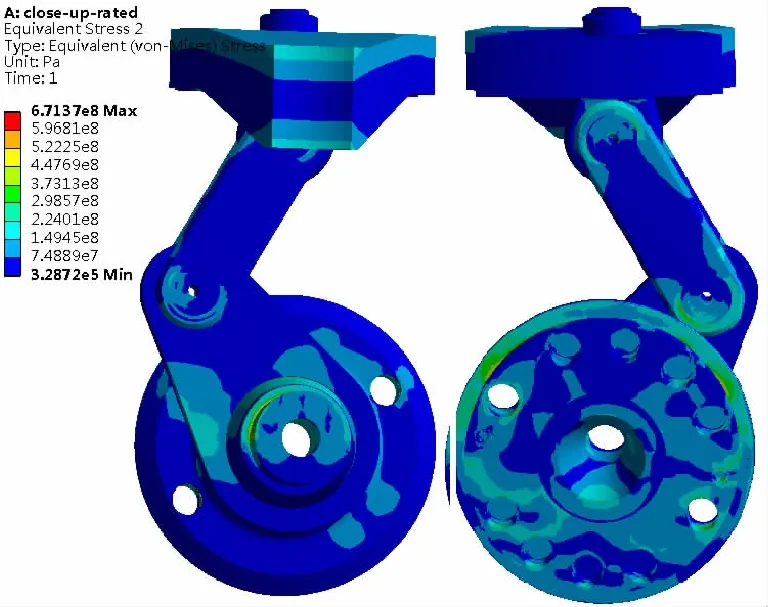
图4 桨叶操作机构联合计算应力结果Fig.4 Conjoint analysis results of blade operating mechanism

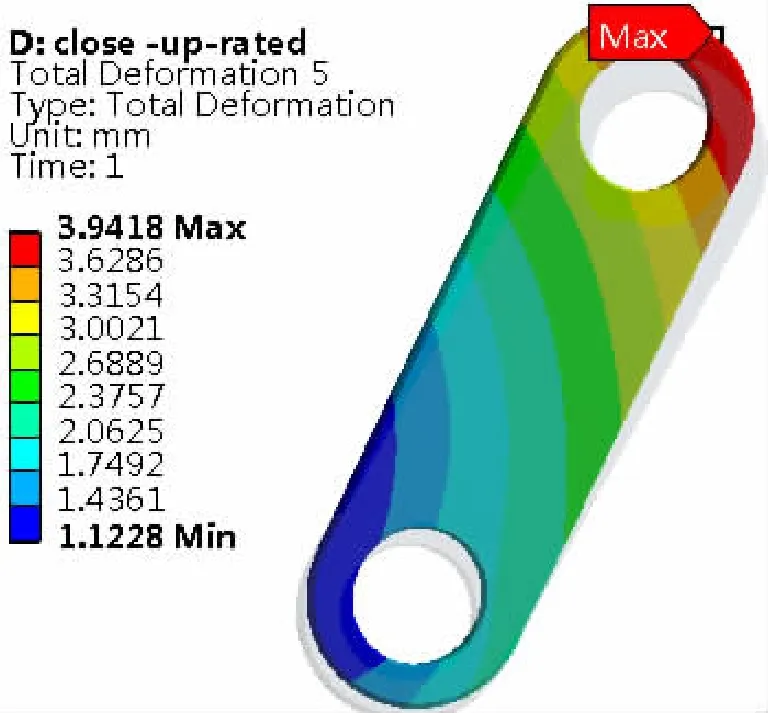
图5 联合分析时连杆合位移Fig.5 Connecting rod resultant displacement in conjoint analysis

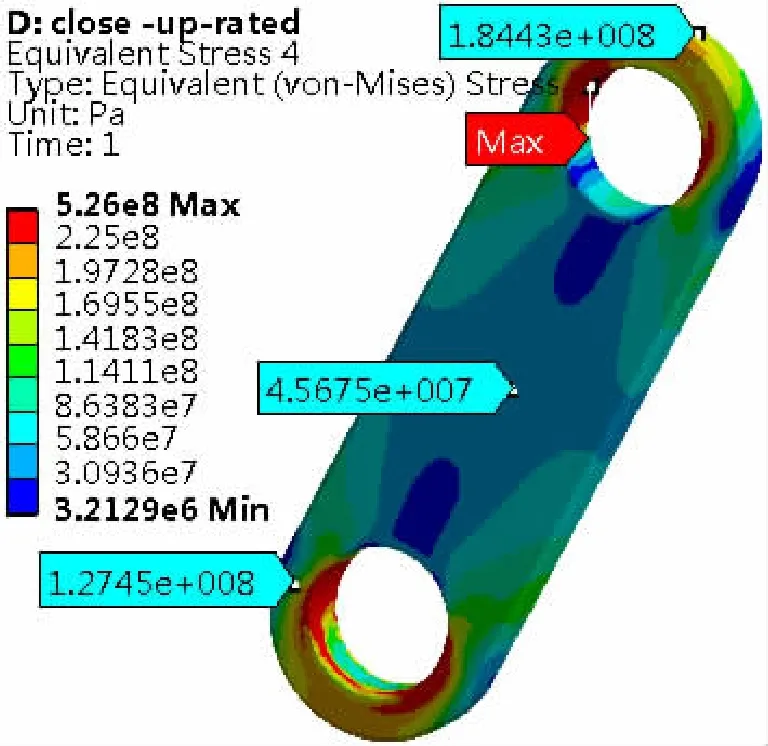
图6 联合分析时连杆等效应力Fig.6 Equivalent stress of connecting rod in conjoint analysis

4 部件单独分析

4.1 有限元模型

以连杆和拐臂为例，单独提取部件有限元模型，如图9、图10所示。

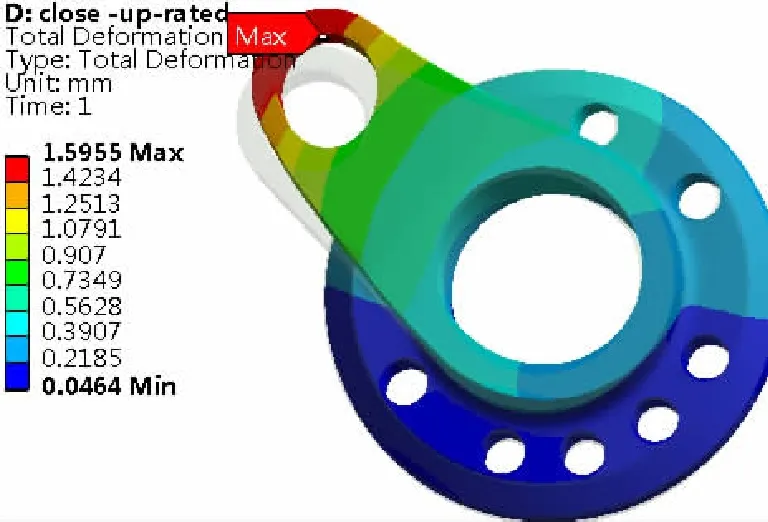
图7 联合分析时拐臂合位移Fig.7 Connecting lever resultant displacement in conjoint analysis

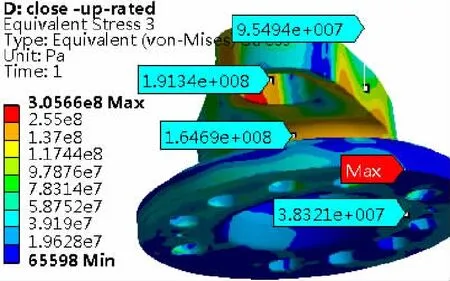
图8 联合分析时拐臂等效应力Fig.8 Equivalent stress of the connecting lever in conjoint analysis

图9 连杆有限元网格 图10 拐臂有限元网格Fig.9 Finite element grid of connecting rodFig.10 Finite element grid of connecting lever

根据连杆的二力杆受力特征，约束连杆的一端销孔，另一端销孔施加拉力；拐臂与枢轴把合处约束转动位移，限制拐臂与轮毂贴合面的径向位移，限制枢轴孔的变形，在拐臂销孔处施加连杆传递的力。根据角度换算连杆和拐臂上的力，保证与联合计算时受力大小一致。

4.2 部件单独计算结果

部件单独计算时：连杆耳柄端最大位移为2.95 mm，为拉伸变形；连杆销孔内应力集中处的最大应力为555.0 MPa，连杆中间应力为47.4 MPa；拐臂最大位移在拐臂端部，为1.38 mm，仅为转动位移；除应力奇异外，拐臂过渡倒圆应力集中处的最大应力为180.0 MPa，拐臂的销孔应力集中处的最大应力为263.0 MPa。计算结果如图11～图14所示。

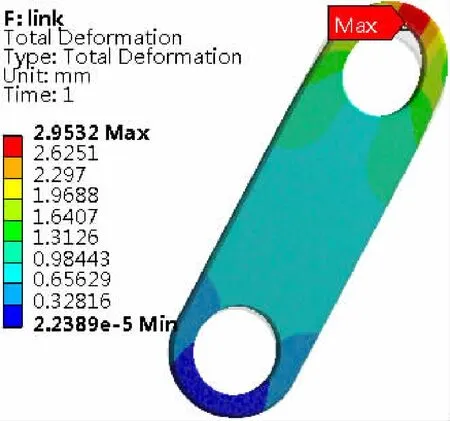
图11 单独分析时连杆合位移Fig.11 Connecting rod resultant displacement during independent analysis

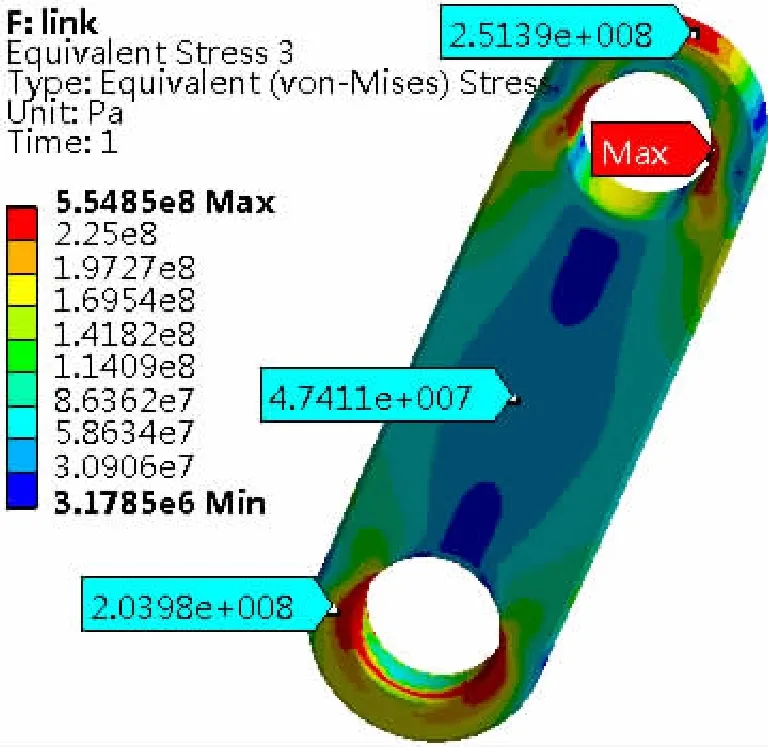
图12 单独分析时连杆等效应力Fig.12 Equivalent stress of connecting rod during independent analysis

图13 单独分析时拐臂合位移Fig.13 Connecting lever resultant displacement during independent analysis

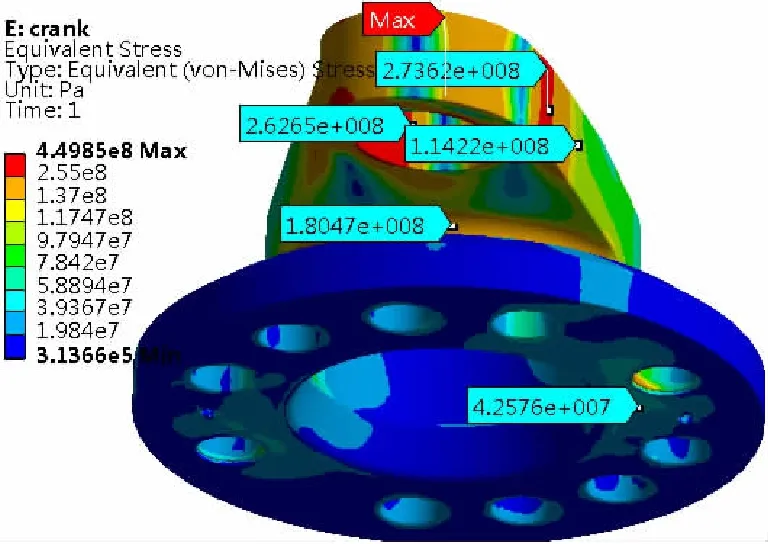
图14 单独分析时拐臂等效应力Fig.14 Equivalent stress of the connecting lever during independent analysis

5 两种分析方法对比

对桨叶操作机构进行联合分析和对部件进行单独分析，得到的各部件具体刚强度计算结果见表1。通过对比可知，较部件单独分析而言，联合分析充分考虑了刚性位移的影响，其位移虽然更大，但变形和应力更小，更符合实际情况。如连杆计算，联合分析能准确捕捉操作机构各部件间的联动，同时体现耳柄螺栓和拐臂的变形，计算结果更接近真实情况的拉伸变形，从而得到更为准确的应力结果。

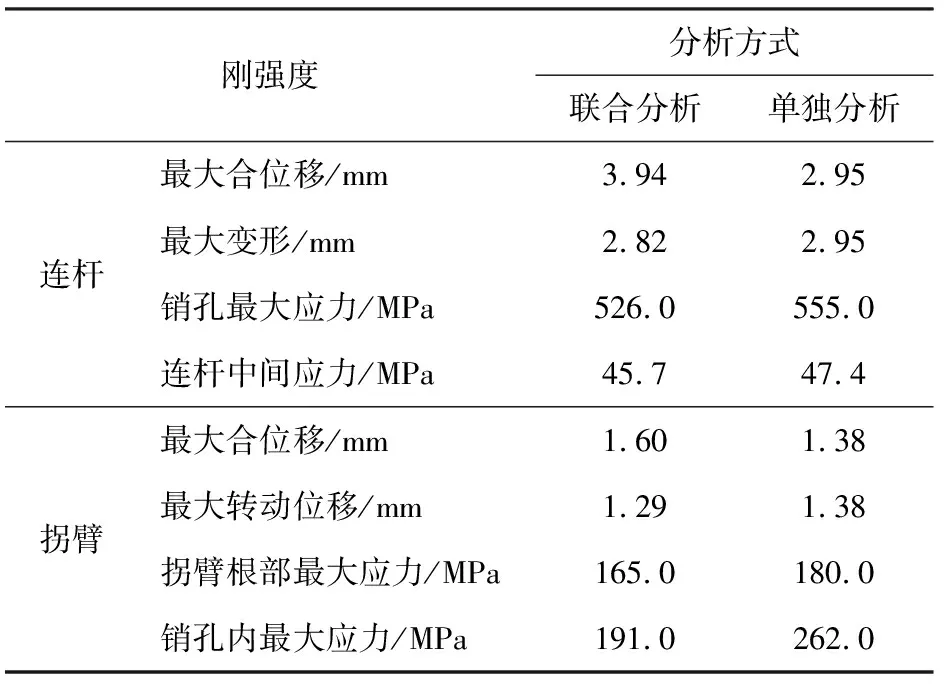
表1 某大型轴流转机组桨叶操作机构各部件刚强度计算结果Tab.1 Strength calculation results of various components of a large Kaplan turbine blade operating mechanism

6 结束语

对某大型轴流转机组的桨叶操作结构进行有限元联合分析，能充分考虑各部件间的协调变形，真实地体现刚性位移边界，符合实际情况，从而得到准确的应力计算结果。而精确的应力结果是确保设计方案安全经济的前提，是产品具备更高市场竞争力的有力保证。对操作结构各部件进行单独分析，虽然简单快速，但因边界限制，使应力值趋于保守，容易导致结构设计安全裕量过大，造成不必要的成本上升，特别是对容量较大的大型机组，会造成材料的极大浪费。

本文的研究，可为多零件构造的组件有限元分析提供参考，对分析工作精度的提高和设计方案的经济性具有积极意义。