一道动量守恒题中速度最大值的探讨

吴琼烟

(莆田第十中学，福建 莆田 351146)

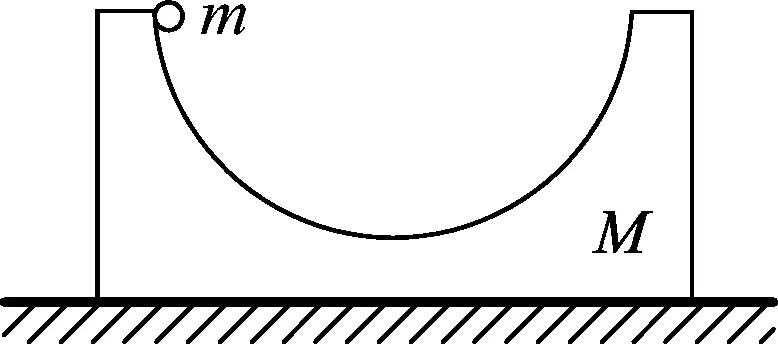
图1

一位学生拿来练习册上的题目,对标准答案中的解答表示质疑．如图1中光滑槽质量为M,静止在光滑水平面上,其内表面为一个半径为R的半球面,质量为m的小球,被细线吊住恰位于槽的边缘处,如将悬绳烧断,小球的最大速度是多少?槽所能发生的最大位移是多少?

学生表示疑惑:小球快到槽底时,虽然水平速度vx还在继续增加,但垂直速度vy却减小,所以合速度未必一直增加,因此小球不是在槽底取得最大速度．

教师觉得学生钻牛角尖了,明明在槽底时速度最大,何必分解为vx和vy来添乱．可是,学生的想法似乎也无法直接否定,于是拿到组内一起讨论．拿到此题时,感觉不难,因为小球速度表达式易求得,所以可以找出最大值,但没想到还是费了一番周折．

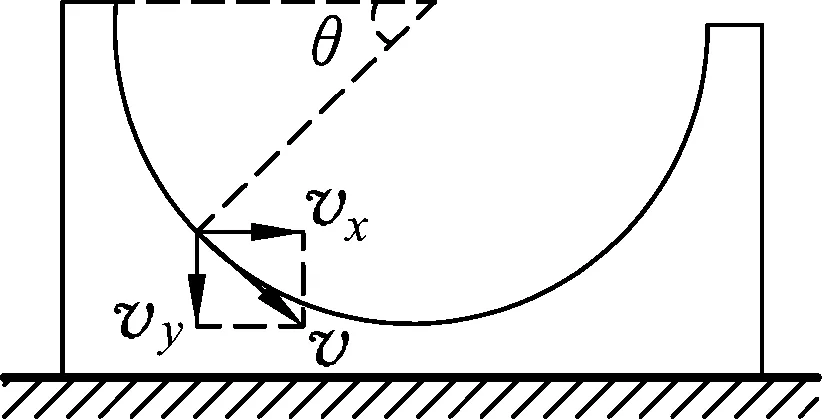
图2

小球下降过程中,槽相对地面速度vx1方向向左,小球相对地面水平速度vx2方向向右．因此小球相对槽的水平速度为vx=vx1+vx2.

小球相对槽的速度为v,如图2分解为水平与垂直方向得关系式

vy=vxcotθ=(vx1+vx2)cotθ.

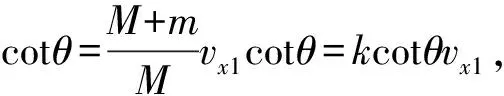
根据动能定理有

把vy和vx2代入后得到

那么小球合速度

v2=vx12+vy2=vx12(1+k2cot2θ)=

(1)

当m≪M时,槽体几乎不动,获得的动能可以忽略,此时m在槽底时速度最大．

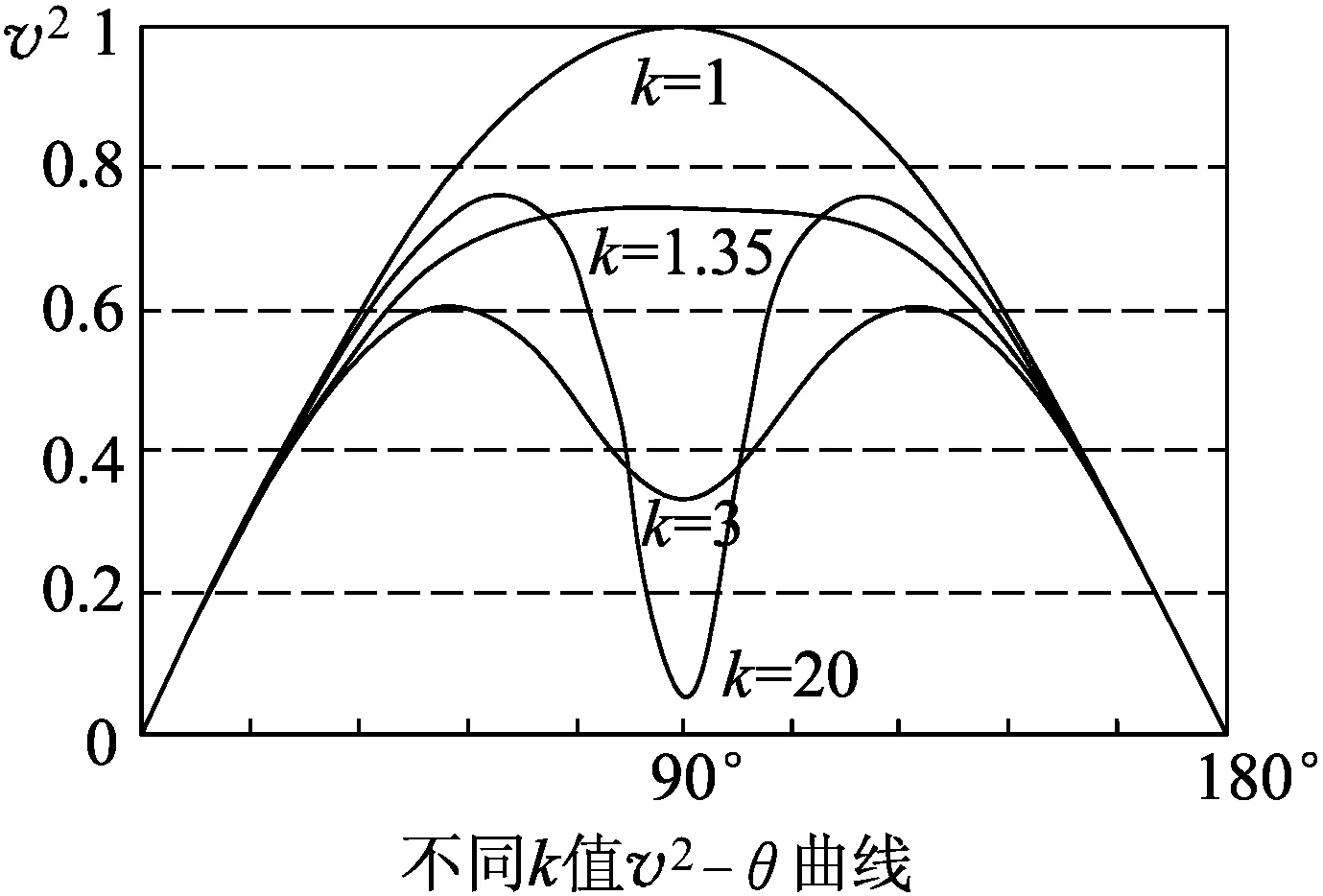
图3

据此我们推定,速度的最大值不在槽底．但后来的事证实这个推定不完全正确．我们借助Excel,采用(1)计算出不同角度的速度平方值,发现k值较小时(如k=1.3)小球下落过程中速度一直增加,极大值发生在槽底(θ=90°)．

化简后得到

(1-k2)(1-k)sin4θ+

k(1-k)(2k+3)sin2θ+k3=0,

(2)

或者cosθ=0.

解方程得

(3)

或者cosθ=0.

(4)

并不是所有的k值都能使得(3)式中的sinθ有解,当k值接近于1时,代入(3)式得到的值可能大于1,θ无解,极大值点应改用(4)式确定．那么k取何值时sinθ有解?我们可以把sin2θ=1代入原方程,得2k2-2k-1=0,解得

看似简单的最大值问题,解题过程却有些曲折．面对学生的质疑,无法直接否定时更应认真对待,想当然的认为标准答案是正确的,可能会错过验算机会．本文采用图像法、求导法、数值分析等方法多途径验算最大值,以确定可靠的结果．