基于科学思维水平层次,培养学生建模能力——以“圆锥摆模型”为例

居 津

(江苏省苏州实验中学，江苏 苏州 215011)

2018年1月,教育部正式发布了《普通高中物理课程标准(2017版)》(以下简称“高中课标2017版”)要求在教学中要让学生体会建构物理模型的思维方法,理解物理模型的适用条件,能通过建构物理模型来研究实际问题,并明确指出引导学生经历物理概念的建构过程和物理规律的形成过程,是发展科学思维的重要途径．同时,高中课标2017版尤其关注学生物理学科核心素养的提升,将科学思维按学业质量要求进行了详细的水平划分,每一水平对于物理模型有不同的、明确的能力要求,具体如图1表示.

图1

高中课标2017版的科学思维对于建构模型的要求划分明确,但由于篇幅限制,课标中并未举例说明如何进行教学实施.本文尝试以“圆锥摆模型”为例,按5个水平要求序化物理教学,谈谈如何逐步提高学生的建模能力和问题解决能力．

1 认识物理模型——萌生建立

科学思维水平1要求学生能说出一些简单的物理模型．著名科学家钱学森指出:模型即使通过对问题现象的分解,利用我们考虑得来的原理吸收一切主要的因素,略去一切次要的因素,所创造出来的一幅图画……高中物理涉及很多物理模型，如:匀变速直线运动,分子动理论等．要培养学生的科学思维能力,就建模、解决问题能力而言,最基本的就是需要了解物理模型的基本规律.我们姑且把此过程称为萌生,即在学生脑中有物理模型的基本原理,以便于在遇到实际问题时可以提取相关信息,解决物理问题,提高学科核心素养．

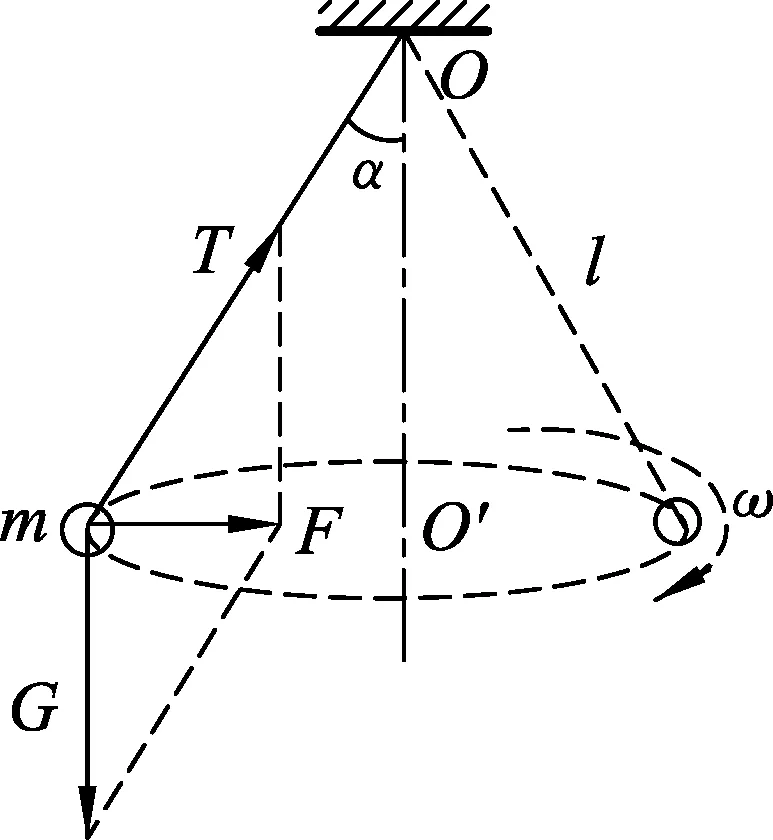
图2

“圆锥摆模型”指细线一端系一小球,另一端固定于天花板,使小球以一定的速度在水平面内做匀速圆周运动,细线在空中所围成的形状类似于圆锥,这就制作成了一个“圆锥摆”． “圆锥摆模型”是匀速圆周运动中一个基本模型,如图2．该模型中,小球受到重力G和绳中拉力T两个力作用,这两个力的合力F提供小球在水平面内做匀速圆周运动的向心力．设绳长为l,小球质量为m,悬线与竖直方向的夹角为α,则向心力F=mgtanα,对于匀速圆周运动的物体,其合外力提供向心力,可以得到

其中r=lsinα.可计算得到

以上是圆锥摆模型的基本规律,只有达到水平1,掌握最简单的原理,萌生建立模型思想,才能达到更高的层次水平,进一步解决较为复杂的问题．

2 应用熟悉的物理模型——运用熟悉

掌握了最基本、最简单的模型后,科学思维水平2要求学生能应用熟悉的物理模型．这就是第二层次即运用．对于这一层次的要求,学生应该能一眼辨识出实际问题与模型的共同点,并用基本物理模型和简单的物理量转化,解决相关问题．

图3

例1.儿童乐园里的游戏“空中飞椅”简化模型如图3所示,座椅通过钢丝绳与顶端转盘连接．已知正常工作时转盘的转速一定．设绳长为l,绳与竖直方向夹角为θ,座椅中人的质量为m．则下列说法正确的是

(A)l变长时,θ将变大.

(B)l变短时,θ将变大.

(C)m越大,θ越小.

(D)m越大,θ越大.

对于以上实际问题,与水平1的基本模型相比,有两处相关变形:(1) 本例题中提到的匀速圆周运动相关物理量是转速n;(2) 圆周运动的半径为r′=lsinθ+r,因此,很快可以得到

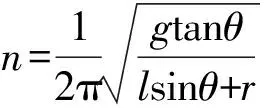
在这一水平层次中,学生的科学思维能力略有提高,不仅要识记基本物理模型,还要在实际问题中应用物理模型,但实际问题与物理模型非常接近,不需要过多的比较或转换．

3 选择恰当的物理模型——分析理解

科学思维水平3要求学生能在熟悉的问题情境中,根据需要选用恰当的模型解决简单的物理问题．这一水平要求明显高于前一层次,重点在于选择,这就需要将问题情境与学生头脑中的众多物理模型进行对比、比较,找出与实际问题最类似的模型,从而解决问题．

图4

例2.如图4所示,杆OO′是竖直放置的转轴,水平轻杆BC的长为L,B端通过铰链与轴相连(它们之间无摩擦),C端固定小球P,细线AC的一端固定在轴上的A点、另一端连在小球P上．已知小球的质量为m,细线AC与轴的夹角θ,重力加速度为g．求:(1)当系统处于静止状态时,杆BC对小球的弹力F1的大小;(2)当轻杆BC对小球的弹力为0时,系统转动角速度ω的大小和细线上的弹力F2的大小;并据此判断当ω变化时细线上的弹力大小是否变化．

在上述物理问题中,有轻杆、有细线,并不是典型的“圆锥摆模型”,第(1)问中,利用静力学知识解决相关实际问题．第(2)问中,考察学生物理学科核心素养科学思维的模型对比能力．当杆中力为0时,小球在细线的作用下随杆OO′发生转动,由小球重力和细线中拉力的合力提供向心力,与“圆锥摆模型”的基本原理完全一致.这需要学生将此问题略作转化,与头脑中的众多模型进行比较,并作出正确的选择,最后将该模型运用到解决本问题中去．在这一层次中,学生需要分析所遇到的场景,对模型加以理解,才能更好地应用解决问题,达到这一层次的学生能力较上一层次有了进一步的提高．

4 将实际问题转换成物理模型——转换提高

图5

例3.蔡氏飞车走壁技艺由著名杂技艺术家蔡少武于20世纪50年代在辽宁省沈阳市创立,是一种在木桶或在环球进行飞车(一般为摩托车或自行车)走壁的高难度表演技艺,集体育与杂技融为一体．为沈阳市第一批市级非物质文化遗产,现仍有蔡氏后人传承这一独特技艺．此表演深受青少年的喜爱,表演者沿表演台的侧壁做匀速圆周运动,如图5．若表演时杂技演员和摩托车的总质量不变,摩托车与侧壁间沿侧壁倾斜方向的摩擦力恰好为零,轨道平面离地面的高度为H,侧壁倾斜角度α不变,则下列说法中正确的是

(A) 摩托车做圆周运动的H越高,向心力越大.

(B) 摩托车做圆周运动的H越高,线速度越大.

(C) 摩托车做圆周运动的H越高,向心力做功越多.

(D) 摩托车对侧壁的压力随高度H变大而减小.

解决物理原始问题,情境教学是培养学生物理学科核心素养的重要渠道．而提高学生科学思维水平的重要表现就是能解决实际问题．物理是最贴近生活的一门学科,建立物理模型的最终目的也就是为了通过解决实际问题,提高学生的问题解决能力,培养关键能力．科学思维水平4要求学生能将实际问题转化成相关物理模型．转换过程一般可以分为以下几个步骤.

4.1 排除干扰因素

上述实际问题中,“蔡氏飞车走壁技艺由著名杂技艺术家蔡少武于20世纪50年代在辽宁省沈阳市创立,是一种在木桶或在环球进行飞车(一般为摩托车或自行车)走壁的高难度表演技艺,集体育与杂技融为一体．为沈阳市第一批市级非物质文化遗产,现仍有蔡氏后人传承这一独特技艺”都属于转换干扰因素,在利用物理模型解决问题时,可以暂且不予理会．

4.2 提取重要信息

本题中的重要信息有4条:(1) 表演者做的是匀速圆周运动;(2) 轨道平面离地面高度不变,即圆周运动的半径不变;(3) 倾角不变,表演者的受力不变．(4) 不受摩擦力作用．

4.3 加工类比

提取重要信息之后,就要对信息进行加工类比,演员受到重力G与斜面支持力F两个力的作用.这两个力的合力提供他做匀速圆周运动所需要的向心力,虽然表面上该问题与圆锥摆不同,但受力的本质是相同的,分析方法也相同．因此,解决这个实际问题,可以应用圆锥摆模型．

4.4 转换应用

通过上述步骤,相信学生对于处理一般的实际问题有了大概的了解,科学思维水平也得到了再次的提高,建模能力和问题解决能力都得到了大大的锻炼．

5 较复杂的实际问题转换成物理模型——抽象领悟

科学思维的最高水平是能将较复杂的实际问题中的对象和过程转换成物理模型．这一层次较上一层次而言,更接近于实际生活,学生遇到的情境更为复杂,学生所具备的能力不仅是转化分析能力,还需要一定的抽象和领悟能力．

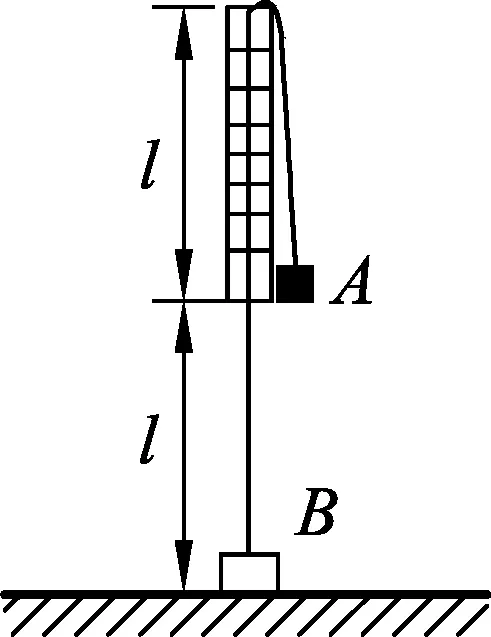
图6

相对于水平4而言,水平5的问题情境更为复杂,但将实际问题转化成物理模型的一般步骤仍然适用．排除无关干扰因素,提取重要信息后,不难发现,小球A最后在水平面内做匀速圆周运动,而向心力是由重力和绳中拉力提供的,由于物块B处于静止状态,所以物块物块B的重力大小与绳中拉力大小相同．只要搞清楚此关键点,那么本问题也就迎刃而解了．此处不再赘述．

对于水平5的能力层次,要求学生具有一定的抽象概括能力,并加以领悟,这显然是所有层次中要求最高的,要达到这个层次要求,必须有意识的在教学中从水平1开始逐步引导,让学生熟悉各种物理模型的不同特点,并不断加深巩固,在简单的实际问题中慢慢加深,从而达到解决复杂实际问题的能力,最终实现科学思维能力的培养,学科核心素养的提高!

以上是笔者基于科学思维水平划分的物理建模能力要求所提出的的一点看法,希望起到抛砖引玉的作用,与广大同仁一起探讨如何提高学生学科核心素养,培养学生建模能力和问题解决能力.