可变形履带式机器人的设计

钱俊泽，杜超平，何振鹏，何 锐，廖 涛，徐唐进

（中国民航大学 a.工程技术训练中心；b.航空工程学院，天津 300300）

随着机器人的应用领域不断扩大，传统机器人由于自身条件的局限性已不能完成某些特殊作业任务。履带式结构具有传动效率高、支撑面积大、越野性能好、牵引附着能力强等诸多优点，适合在危险恶劣环境下工作。近年来国内外开始重视对履带式机器人的结构设计研究，但由于履带式机器人设计及控制算法复杂，其应用仍具有局限性。因此，深入开展履带式机器人的研究，对提高其结构性能和执行任务的可靠性具有重要意义。

结构设计方面，中国研制的“灵蜥-B”机器人，设置3段履带作为行走装置，可越过40 cm高度障碍[1]。为充分发挥轮式结构的快速性，突出履带式结构良好的地面适应性，Michaud等[2]和中科院沈阳自动化研究所分别研制了Andros系列机器人和轮-腿-履带复合移动排爆机器人[3]。为使履带式机器人具有灵活的物理结构及良好的环境适应能力和生存能力，国内外学者对机器人的体系结构和变形策略开展了研究，设计了Single-Tracked机器人[4]、VGTV机器人[5]和CEBOT机器人[6]，提出了建立在连接规划和路径规划之上的运动规划方法。总体看来，国内外学者对履带式机器人的结构设计和控制算法开展了深入研究，但还存在一些不足，主要如下：①体积和重量太大；②越障能力差，越障高度有限；③与外部通信的研究不够深入；④机动性和灵活性需进一步提高。

针对上述不足，通过理论计算设计出可变形履带式机器人机构模型，基于SolidWorks三维建模平台建立可变形履带式机器人的三维模型。为深入研究该机器人的结构可靠性，以其前调节杆为研究对象，建立有限元模型，进行结构优化设计，达到轻量化目的，设计了传动系统和控制系统，开发了机器人控制界面，最后进行了实物制作。

1 履带式机器人机构设计及传动系统布置

设计的可变形履带式机器人由1个控制模块（包括控制电路和驱动电机）和2个相同的可变形履带移动单元模块组成。

1.1 机构设计

机器人的机构设计简图如图1所示。履带轮部件由四连杆机构（前调节杆、后调节杆、调节短杆、机架）构成，履带由带轮 A1、A2、A3、A4共同支撑，其中 A1为驱动轮。该结构可保证在遇到较大障碍物时，机器人可通过驱动前调节杆旋转来调整履带的几何形状，实现越障功能。

图1 履带机器人结构示意简图Fig.1 Schematic diagram of crawler robot structure

1.2 传动系统布置

机器人移动单元模块的传动系统简图如图2所示。电机输出的动力经过齿轮G1带动G2传递到G3，G3带动G4传递到同步带轮C1，接着通过同步带CL1传递到同步带轮C2，驱动带轮A1运动。

传动系统齿轮G3和G4的运转方向如图3所示。弹簧连接在车体与前调节杆之间，在平坦路面运动时，由于受到弹簧的约束，前调节杆在弹簧力与齿轮G3反作用力之间维持平衡，保持既定姿态不变。当行进中遇到障碍时，弹簧力与齿轮G3反作用力的平衡关系被打破，前调节杆向上抬起使得履带变形越过障碍，在越过障碍到达平坦路面时移动单元模块的机构在弹力作用下恢复到平地运动姿态。

图2 传动系统布置图Fig.2 Transmission system layout

图3 传动系统齿轮受力图Fig.3 Force diagram of transmission gear

该驱动系统使得复合单元模块的移动机构能在1个驱动力的作用下根据不同的约束环境来实现履带的变形越障。

2 可变形履带移动单元模块的机构参数

在越障过程中，可变形履带移动单元各模块构件间会发生相对运动，为满足移动单元模块在越障过程中姿态的调整以及履带不脱带，要保证履带在形状变化过程中长度形变量尽可能小，对影响履带长度变化的履带支撑机构参数进行分析，如图4所示。

图4 履带机器人机构参数Fig.4 Crawler robot mechanism parameter

在主轴轴心O处建立Oxy平面坐标系，其中x轴与 OD 重合，y 轴与 O2O3垂直。图 4 中点 O1、O2、O3、O4分别为轮 A1、A2、A3、A4的轮心，其他各参数释义如表 1所示。

表1 轮履复合移动单元的机构参数Tab.1 Mechanism parameters of wheeled compound mobile units

3 履带轮的机构参数分析

轮心 O1、O2、O3、O4和点 B、C、D 的向量的表达式可写为

调节短杆CD与车体OD的夹角γ随前调节杆OB与车体OD的夹角α的变化而变化。将式（6）和式（7）合并整理可得γ与α的关系为

由式（8）可知调节短杆CD与车体OD的夹角γ随 α 的变化而变化，可设与带轮 A1、A2、A3、A4相切的线段A1A2、A2A3、A3A4、A4A1分别为l10（α）、l20（α）、l30（α）、l40（α），与履带支撑轮相接触的履带长度为lc（α），则履带总长度l（α）表达式为

其中，l10（α）、l20（α）、l30（α）、l40（α）、lc（α）与机构参数的关系可表示为

对影响履带长度的主要参数r、r0、m、h进行分析：当轮A3的半径r分别取25 mm、35 mm、45 mm时，履带长度（lα）随夹角α的变化关系，如图5所示；当轮A2的半径r0分别取10 mm、15 mm、20 mm时，履带长度（lα）随夹角 α 的变化关系，如图6所示；轮A2、A3的中心距m分别取80mm、100mm、120mm时，履带长度l（α）随夹角α的变化关系，如图7所示；主轴中心与机架垂直距离h分别取25 mm、35 mm、45 mm时，履带长度（lα）随夹角α的变化关系，如图8所示。

在设计过程中参数取的实际值为：r=25 mm、r0=20 mm、m=80 mm、h=25 mm，这可以保证机器人正常运动时不受履带变形量影响。考虑到机器人的装配精度和履带自身形变对机构运动性能的影响，取履带的实际长度l=720 mm。

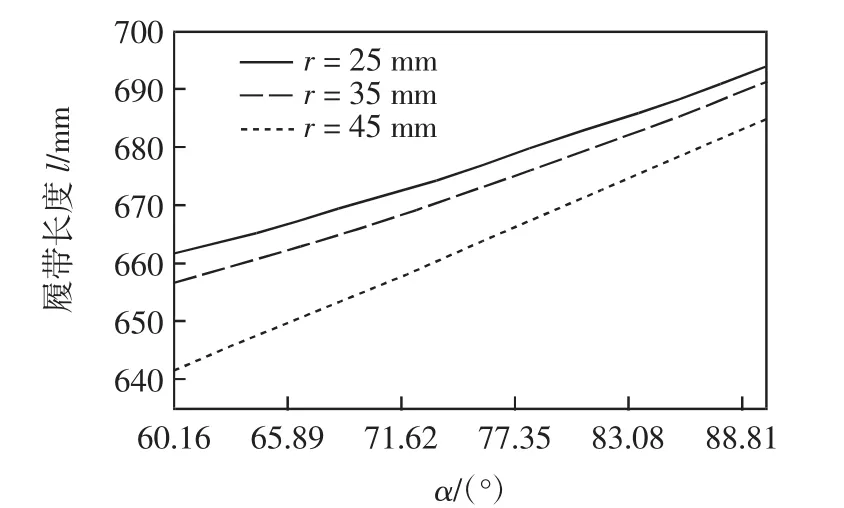
图5 不同r下履带长度l随夹角α的变化Fig.5 Track length changes with angle α under different r

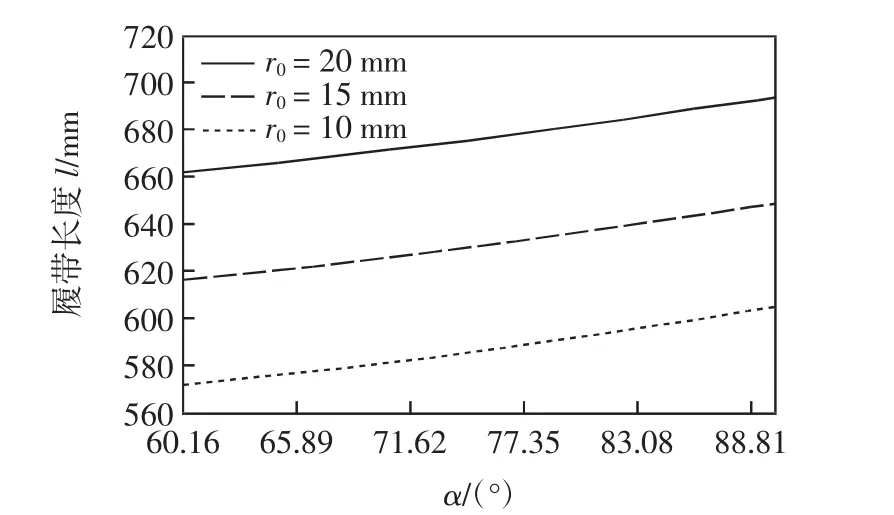
图6 不同r0下履带长度l随夹角α的变化Fig.6 Track length changes with angle α when r0is different

图7 不同m下履带长度l随夹角α的变化Fig.7 Track length changes with angle α under different m

图8 不同h下履带长度l随夹角α的变化Fig.8 Track length changes with angle α under different h

4 履带式机器人结构优化设计

4.1 拓扑优化数学模型

拓扑优化设计三要素包括：设计变量、约束条件和优化目标，则优化设计的数学模型可描述为

约束条件为

其中：E（x）为期望优化目标；xi为离散设计变量单元密度或厚度；Ki为单元刚度；u、f为节点位移和节点力向量；λc和c为结构的性能约束（应力或应变）；Vi和V分别为单元体积和总体积；xmin和xmax分别为约束变量xc上下限[7]。对前调节杆的优化三要素设定如表2所示。

表2 调节杆的优化三要素设定Tab.2 Three parameters for adjusting bar optimization

4.2 前调节杆拓扑优化

前调节杆是机器人四连杆机构的重要组成部分，在前进中承受的载荷和冲击最大，对其进行结构拓扑优化，在满足强度要求的前提下达到轻量化的设计目标，对机器人后续制作具有实际意义。

分析前调节杆之前，先在三维建模软件Solidworks中建立前调节杆的实体模型，再导入到Hypermesh中对模型进行相关参数设置，逐步对前调节杆进行六面体网格划分,前调节杆有限元模型如图9所示。

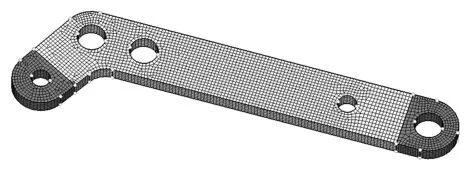
图9 前调节杆有限元模型Fig.9 Finite element model of front adjusting bar

分析前调节杆受力，约束孔1和孔2的5个自由度，并在孔3～5的内壁施加压力，如图10所示，其值分别为 20 MPa、40 MPa、10 MPa。

图10 前调节杆载荷分布示意图Fig.10 Load distribution on front adjusting bar

经18次迭代后得到的拓扑优化密度云图如图11所示。密度云图显示此模型中密度值为1的部分，其余部分从视图中删除。

图11 前调节杆拓扑优化结果Fig.11 Optimized topology of front adjusting bar

从优化后的材料分布结果图可得到结构调整后的前调节杆几何模型，如图12所示。

图12 优化后前调节杆几何模型Fig.12 Geometry model of optimized front adjusting bar

在上述约束和载荷条件下，对前调节杆进行静力分析，其应力云图如图13～图15所示。

图13 前调节杆在Press 1下的应力分布Fig.13 Stress distribution on front adjusting bar under Press One

图14 前调节杆在Press 2下的应力分布Fig.14 Stress distribution on front adjusting bar under Press Two

图15 前调节杆在Press 3下的应力分布Fig.15 Stress distribution on front adjusting bar under Press Three

由以上可知，在承受载荷Press 1、Press 2、Press 3的情况下，前调节杆均在压力所施加的轴承孔内达到应力最大值，其值为41.11 MPa。亚克力板拉伸强度在55～77 MPa水平，弯曲强度在 90～130 MPa水平，满足强度设计要求。

将拓扑优化理论应用于机器人机构部件的设计，在保证其结构性能的基础上大大减轻了部件的质量。利用拓扑优化后的密度云图，可以确定前调节杆轻量化后的基本形状，为后续实物制作提供参考，使其更加满足设计要求。

5 履带式机器人控制系统设计及样机搭建

控制部分包含控制界面、wifi数传模块、单片机、外设以及电源电路5大部分。控制界面由Microsoft Visual Studio基于开源代码编写而成，其主要功能是向下位机发送指令集并产生实时响应[8]；控制指令由包头FF、数据位、包尾FF构成，单片机识别包头包尾后进入Fuction函数进行比对数据位，进而进入相应的外设控制函数，无包头包尾的指令视为空指令，单片机识别后不产生任何有效控制；控制页面编写过程中嵌入wifi视频的网络地址，从而实现视频从网页到页面显示的过渡[9]。主控制界面如图16所示。

图16 主控制界面Fig.16 Main control interface

采用MTK7620N为wifi模块主芯片，支持IEEE 802.11.b/g/n协议传输数据，基于MIPS24Kc内核，产生580 kHz主频，支持2.4 G频段MIMO，实现最高300 Mbps的传输速度。供电后wifi模块发出信号供上位机连接，当控制页面连接上wifi信号后即可发送指令。接收到上位机的指令后wifi模块通过串口通信（模块的RX与TX和单片机的串口1RX、TX对接）从而传输到单片机进行指令识别并产生有效控制。wifi模块接收到上位机的指令后通过串口通信（模块的RX与TX和单片机的串口1RX、TX对接）传输到单片机进行指令识别并产生有效控制[10]。

单片机采用STM32F1ZET6大容量芯片作为主控芯片，ZET6有丰富的片上资源：8个定时器以及多路ADC和DAC、多个高速I/O。当单片机识别指令后进入Fuction函数进行匹配数据位，数据由6位构成：前2位为外设选择位；中间2位为外设号选择位；后2位为参量设置位。单片机识别上位机发出的有效指令后，产生一次相关外设函数的调用，如需连续控制，上位机则需要连续发送指令。

外设包含wifi视频，2个9 G云台舵机，4个MG996大扭矩舵机、2个10 KG/CM扭矩的减速电机。wifi视频用于实时路况与环境监测，其中：2个云台舵机提供两自由度采集角度；4个MG996舵机组合成四自由度的机械手，模拟人类手夹持物体的动作；2个大扭矩减速电机提供履带车的源动力。

电源电路包含5节串联的18650大容量锂电池、2块LM2596降压稳压电路、L298N电机驱动模块以及限流保护电路。1块LM2596用于L298N及电机供电，另1块用于单片机及剩余外设供电。

考虑外设同时工作时电路的峰值电流可能超过单个芯片的承受上限，故在并联支路上串联电流检测模块，当电流超过3 A（降压芯片所能承受的最大电流）时给单片机1个反馈信号切断相应支路，以达到保护电路的目的。可变形履带式机器人的实物样机如图17所示。

图17 可变形履带式机器人样机Fig.17 Prototype of deformable tracked robot

6 结语

1）提出了一种可变形履带机器人的结构并介绍其设计思路，运用理论推导、参数优化分析等方法确定了轮-履复合移动单元模块的机构参数。通过数值计算分析了越障性能与结构参数的关系，对影响履带长度变化的履带支撑机构参数进行了可行性分析。

2）以机器人重要部件的四连杆机构进行优化设计，建立有限元优化模型，以应力和重量为优化目标，运用有限元法对主要结构进行拓扑优化。结果表明，在满足其强度要求的前提下达到了轻量化的设计目标，为机器人实物制作提供技术参考。

3）对履带式机器人进行结构设计并结合软件控制界面、wifi数传模块、单片机、外设以及电源电路进行样机制作，结果表明该履带式机器人可利用远程无线网络进行传输控制，后续将结合北斗定位进一步提升其信号传输功能。