城市道路未来车速预测模型研究
2019-01-24杨马英李一飞
杨马英,楼 挺,李一飞
1 (浙江工业大学 信息工程学院,杭州 310023)2 (浙江工业大学 计算机科学与技术学院,杭州 310023)
1 引 言
交通拥堵是一种常见的现象,在许多城市中这已经成为一种城市病.交通拥堵直接造成了城市的整体运转效率降低,间接的导致了经济损失.根据中国交通部发表的数据显示,交通拥堵带来的经济损失占城市人口可支配收入的20%,相当于每年国内生产总值损失5-8%,每年达2500亿元人民币.如果可以准确预测道路未来的车速,那么在拥堵发生之前就可以采取预防措施来帮助解决拥堵问题.
预测道路未来的车速是一个具有挑战性的问题,道路未来的车速受到以下三个因素影响:1.空间依赖.一段道路的车速受到其上游的车速和下游的车速的影响.2.时间依赖.一段道路的车速受到上个时间段道路车速的影响.特定的时间点也会影响道路车速,例如工作日的早高峰和晚高峰车速会下降.3.其他因素.例如在下雨、大雾等天气情况下,道路车速会较慢.节假日也会影响道路车速.
目前国内外对于交通拥堵预测的诸多研究,主要有基于时间序列相关的预测分析[1,2]、向量自回归方法[3]、神经网络预测[4,15,16]、贝叶斯网络预测等方法[5,6].这类方法的研究多见于理论研究,且由于其立足的基础理论在处理大数据上缺少鲁棒性,所以导致模型普遍缺乏长效性和扩展能力[7].
深度学习可以让那些拥有多个处理层的计算模型来学习具有多层次抽象的数据的表示.这些方法在许多方面都带来了显著的改善,包括最先进的语音识别、视觉对象识别、对象检测和许多其它领域,例如药物发现和基因组学等[8].LSTM(Long Short-Term Memory)是深度学习中的一种方法,它适合解决时间序列输入输出问题[9],因此十分适用于解决道路车速预测问题.本文应用LSTM网络来处理具有时空特性的道路车速信息,结合神经网络中的全连接层来融合外部因素,构建了一个端对端的基于LSTM的道路未来车速预测模型研究(FSPOL).
2 道路车速估计
预测道路车速首先需要能准确估计道路的平均车速,浮动车技术是目前常用的获取道路交通信息技术手段之一,而出租车GPS 数据是该技术重要数据来源.许多城市的出租车都安装了GPS 设备,这些设备往往以较小的时间间隔持续的向出租车管理部门上传车辆序号、车牌号码、GPS时间、车辆行驶状态(载客,空载)、精度、纬度等数据.由于出租车长时间、大范围的城市出行特点,安装有 GPS 设备的出租车通常被视为流动的检测器,能够很好的反应城市全局路网的交通动态,一定程度上克服了定点设备检测范围有限、成本昂贵、建设困难等缺点[10].本文以出租车轨迹数据来估算道路的平均车速.
2.1 GPS数据轨迹化
车辆行驶轨迹Traj可以定义以下一个多元组:
Traj=
(1)
公式(1)中pi,i∈[1,n]为车辆行驶轨迹上的任意一个定位点,包含空间位置信息,时间信息等,并按照编号由小到大依时间先后顺序排列.生成轨迹的过程如下:
1.根据车辆ID将GPS数据按时间先后排序,按先后顺序去取GPS数据;
2.新建轨迹Traj(Traj是一个包含按时间排序的车辆GPS数据的集合),并将当前GPS数据加入Traj中;
3.取下一条GPS数据,如果此GPS数据与当前Traj中车辆的ID不同则执行步骤2;否则执行步骤4;
4.将当前GPS数据加入到Traj中,执行步骤3;
5.最后我们可以得到根据车辆ID区分的轨迹数据集.
2.2 出租车GPS数据的时空划分
城市道路车辆的速度具有明显的时间特性和空间特性.在时间上,同一天中未来某时段的运行速度受到上一个时段及上几个时段等多个历史时段运行速度的影响,在同一周内,工作日某一时段的运行速度受到前几个工作日该时段运行速度的影响,具体表现为速度的周相似性,已有研究表明运行速度的周相似性程度较高,具有很强的规律性;在空间上,由于路网的连通性,上游道路的运行速度会直接影响到下游道路的运行速度,下游道路交通阻塞等情况也会影响上游道路车辆的运行速度.因此,路段下一时段的运行速度不仅与该路段当前时段的速度数据及历史速度数据有关,同时也与其上下游路段当前时段的速度数据及历史速度数据有关.因此需要对GPS轨迹数据进行时间和空间上的划分,得到预测所需的时间、空间信息.
在每一条GPS数据中都有时间信息,因此很容易可以对轨迹进行时间划分.GPS数据的空间划分是将GPS数据和具体的路段联系起来,目前针对GPS 数据的地图匹配算法有:基于道路几何信息的匹配算法、基于概率统计的匹配算法以及基于卡尔曼滤波的匹配算法,基于人工神经网络的匹配算法等.除了基于道路几何信息的匹配算法,其他算法复杂性相对较高,因而对于实时性要求高、数据量较大、行驶道路环境复杂多变的出租车,这些种算法很难符合要求.一般一小段道路在地图中可以认为是一个平行四边形,因此本文采用平行四边形框来选取经过道路的GPS轨迹[11].
2.3 道路平均车速估计
对于每个路段在每个时间段中的轨迹数据,我们可以用来估算平均车速.要计算一个路段的平均速度首先需要计算每一条轨迹的速度,每一条轨迹Traj的车速计算方法如公式(2):
(2)
可以采用欧氏距离计算小范围内两点之间的距离,计算方法如公式(3)所示:
(3)
公式(3)中,xi和yi表示pi中的空间位置信息.由于采集数据中难免会有误差,因此需要将异常的速度数据予以删除,保证轨迹速度数据有效,本文采用四分位法去除异常.每个路段的平均速度的计算如公式(4)所示:
(4)
公式(4)中,vi表示轨迹i的速度.但是上述方法较容易受到高速,低速样本对终结果带来的影响.考虑行程距离的因素可以使结果更加精确[12],计算方法如公式(5)所示:
(5)
公式(5)中Li表示轨迹走过的总路程.
3 预测特征的选择
同一天中未来某时段的运行速度受到上一个时段及上几个时段运行速度的影响.在一周内,工作日某一时段的运行速度受到前几个工作日该时段运行速度的影响.空间上,由于路网的连通性,上游道路的运行速度会影响到下游道路的速度.反过来,下游道路交通阻塞也会影响上游道路车辆的运行速度.因此,某一路段下一个时段的运行速度不仅与该路段当前时段的速度及历史速度有关,同时也与其上下游路段当前时段的速度及历史速度有关.基于上述考虑,在对速度进行短时预测时,不仅仅考虑当前路段当前时段及前几个时段的运行速度,还考虑了该路段上下游、和上周同一天的当前时段和前几个时段的运行速度.某路段在t+T时段的运行速度如公式(6)所示:
(6)
公式(6)中,F表示一种非线性函数关系;t表示当前时刻;T表示时间隔;vs,vx分别为上下游路段的平均运行速度值;vW为预测路段上周同一天相同时段的平均运行速度;n可以称为时段参数,表示选择前n个时段的道路车速特征来预测未来车速.
道路的车速会受到许多其他因素的影响,例如天气事件.图1(a)展示了在下雨天和晴天的道路平均车速.从图中可以看出雨天时大部分时间段道路的平均车速低于晴天.
道路的车速还会受节假日的影响,上图展示了工作日和周末的道路平均车速.从图中可以看出工作日的道路车速高峰在早上9点左右,晚高峰在晚上6点左右,而工作日则没有明显的早高峰和晚高峰.本文选取天气和星期几作为额外特征fext来提升道路预测精度.
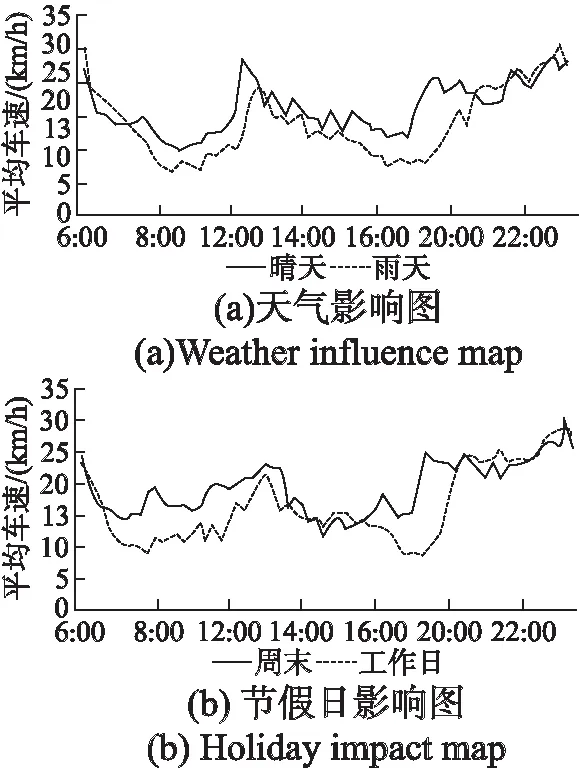
图1 不同天气和日期情况下的道路车速状况图Fig.1 Road speed chart under different weather and date conditions
4 预测模型的设计
RNN网络的结构如图2所示.RNN 可以被看作是同一神经网络的多次复制,每个神经网络模块会把消息传递给下一个,RNN的这种结构适用于处理时序数据.
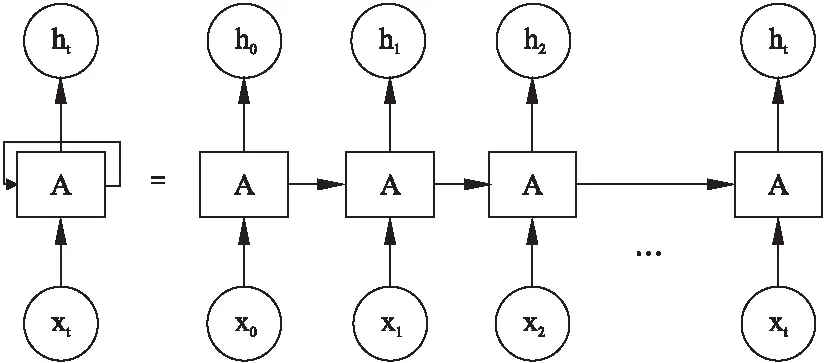
图2 RNN网络结构图Fig.2 RNN network structure diagram
LSTM是一种特殊类型的RNN,它继承了大部分RNN模型的特性,同时解决了梯度反传过程由于逐步缩减而产生的梯度消散问题[9].LSTM的基本单元是一个细胞和三个门,分别是输入门(input gate),遗忘门(forget gate)和输出门(output gate),如图3所示.输入门是将新的信息选择性的记录到细胞状态中.遗忘门是将细胞状态中的信息选择性的遗忘.输出门是用来控制细胞的输出值.通过这三个门的协作,可以使细胞中包含的信息不断的更新和遗忘,因此十分适用于处理时序数据.

图3 LSTM网络结构图Fig.3 LSTM network structure diagram
道路未来的车辆行使速度和之前时段的车辆行使速度有很大的关系,预测选取的预测特征具有时序信息,因此可以用LSTM来进行道路车速预测.
本文预测道路所选取特征包括当前路段当前时段及前几个时段的行使速度,还考虑了该路段上下游、上周同一天的当前时段和前几个时段的运行速度,这些特征都是时序数据,因此考虑使用LSTM来处理每一种时序数据提取特征.
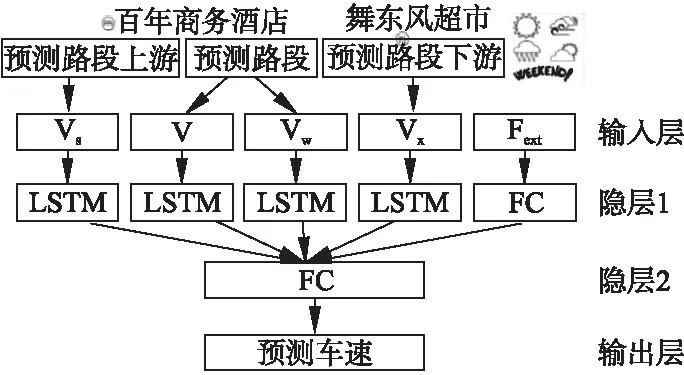
图4 模型结构图Fig.4 Model structure diagram
本文设计模型如图4所示,图4中,Vs代表上游路段的时空特征,V代表需预测路段的时空特征,VW代表需预测路段上周同一天的时空特征,Vx表示下游路段的时空特征.FC单元表示神经网络中的全连接层.天气类型共有阴、晴、小雨、多云等15种.天气信息映射成一个15维的特征向量,星期信息映射成一个7维向量,因此Fext是一个22维的特征向量.模型各层的特征维度信息如表1所示.
表1 模型各层的特征维度信息
Table 1 Feature dimension information of each layer of the model

输入层Vs(1,n)V(1,n)VW(1,n)Vx(1,n)Fext(1,22)隐层1输出(1,n)(1,n)(1,n)(1,n)(1,10)隐层2输入(1,4∗n+10)隐层2输出(1,5)
表1中n为时段参数,表示选择前n个时段的道路车速特征来预测未来车速.
模型采用均方根误差(RMSE)作为预测误差,如公式(7)所示:
(7)
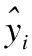
训练中batch的最小值设置为64,训练的终止条件设置为迭代训练10000次.
表2 模型训练方法表
Table 2 Table of model training method

模型训练算法:输入:按照时空划分的道路平均速度:{V0,v1,…,V179}其他特征:{fext}时间段参数:n输出:训练好的模型//准备训练样本初始化T—>0Fori(n 原始数据包括成都市1.4万辆出租车的超过14亿条GPS记录.这些GPS记录的时间范围从2014年8月3日开始,到2014年8月30日为止,中间缺失了8月7日,8月13日,8月17日.这些数据已经经过了初步处理,清洗掉了其中重复和异常的记录,并忽略了00:00:00~05:59:59这一时间段的记录.已掌握的数据包括三个部分:1)出租车GPS数据;2)道路轨迹数据;3)用于辅助识别轨迹对应的前一小时的GPS记录数据,其中乘客状态1表示载客,0表示无客,如表3所示. 表3 出租车GPS数据示例表 出租车ID纬度经度载客状态时间点112230.4996330.4936530.6319730.63188103.97717104.00362104.03840104.03667110106:01:2206:02:2206:01:1306:02:53 本文选取了成都市一环路、二环高架路、人民路、蜀都大道等10多条道路上的100个路段为研究对象.实验中定义路段长为500米,时间段设置为10分钟.实验中样本的总数量受到如下因素的影响:是否有前一周当时的道路车速数据(共16天可提供完整数据)时段参数n的影响(n太小则缺少之前时段的信息,会导致预测不准确,n太大则会有太多和下一时段不相关的信息影响下一时段车速的预测,因此考虑n∈[3,10],共约270000的样本数量).本文在实验中随机挑选70%的样本作为训练数据,剩下的30%作为测试数据,如表4所示,误差通过公式(13)计算. 表4 不同时段参数下模型的精度表 n训练集误差测试集误差3456789103.693.613.213.573.183.503.234.145.464.924.524.904.564.994.745.09 首先验证了当n∈[3,10]时模型在整个数据集上的精度.从表3可以看出当n=7时,训练集误差最小为3.18.当n=5时测试集误差最小为4.52.从总体上来看,当n∈[3,10]时,训练集误差和测试集误差非常接近,因此本文提出的模型鲁棒性较强,受参数的影响较小. 图5 模型预测展示图Fig.5 Diagram of model predictive display 图5展示了n=5时本文方法的预测结果,横坐标为时间,纵坐标为汽车行驶速度,从图上的结果可以看出预测结果和实际结果较为接近,表明本文方法取得了较良好的预测结果. 为验证本文方法(FSPOL)的性能,选择目前比较优秀的四个模型进行对比: 1.ARIMA(Auto-Regressive Integrated Moving Average):一种用来处理时序数据的常用模型[1,2]. 2.VAR(Vector Auto-Regressive):一种可以处理时空数据的模型,它可以发现输入特征之间的关联,但是这个方法的参数较多,计算量较大[3]. 3.RBF(Radial Basis Function Network):径向基神经网络是一种前馈反向传播网络,是一种可以在高维空间内插值并可以进行局部逼近的神经网络,这种网络训练速度快,适合一些实时性较强的场合[14]. 4.DBN(Deep Belief Network):深度信念网络(DBN)是深度学习中一个非常成功的模型.DBN采用无监督的预训练方法,对于噪声具有很好的稳定性,可以达到很小的均方误差和很高的识别率[15]. 本文方法(FSPOL,n=5)和上述四种传统的方法比较实验结果如表5所示,误差通过公式(13)计算得到. 表5 不同方法的预测精度表 方法训练集误差测试集误差ARIMAVARRBFDBNFSPOL 7.743.610.13.183.218.284.9517.224.894.52 实验结果表明 ARIMA和RBF方法在总误差的表现上差于其他三种方法.RBF方法训练集的误差只有0.1,但是在测试集上的误差确达到了17.22,模型出现了过拟合现象.本文方法在测试集误差上均取得了最佳的结果.可以认为本文方法取得了优于其他4种方法的预测结果.另外本文方法的训练集误差和测试集误差的差值是最小的,这说明本文方法的泛化性能较强. 预测道路未来车速受限需要解决道路车速估计的问题,本文采用浮动车技术来估计道路车速.在时间上,道路未来的车速受前几个时段的车速的影响;在空间上,道路未来的车速受当前道路上游、下游道路的影响,因此本文选取了时空特征来预测未来车速,并用LSTM来处理这些时空特征.道路未来的车速还受到天气,节假日等因素的影响,采用神经网络中的全连接层来融合这些特征.本文基于成都市的数据进行了验证,结果表明本文提出的模型鲁棒性较强,模型的泛化性能较强,模型的预测精度较高.5 仿真和验证
5.1 数据
Table 3 Sample table of taxi GPS data
Table 4 Accuracy table of the model under different time interval parameter
5.2 实验结果
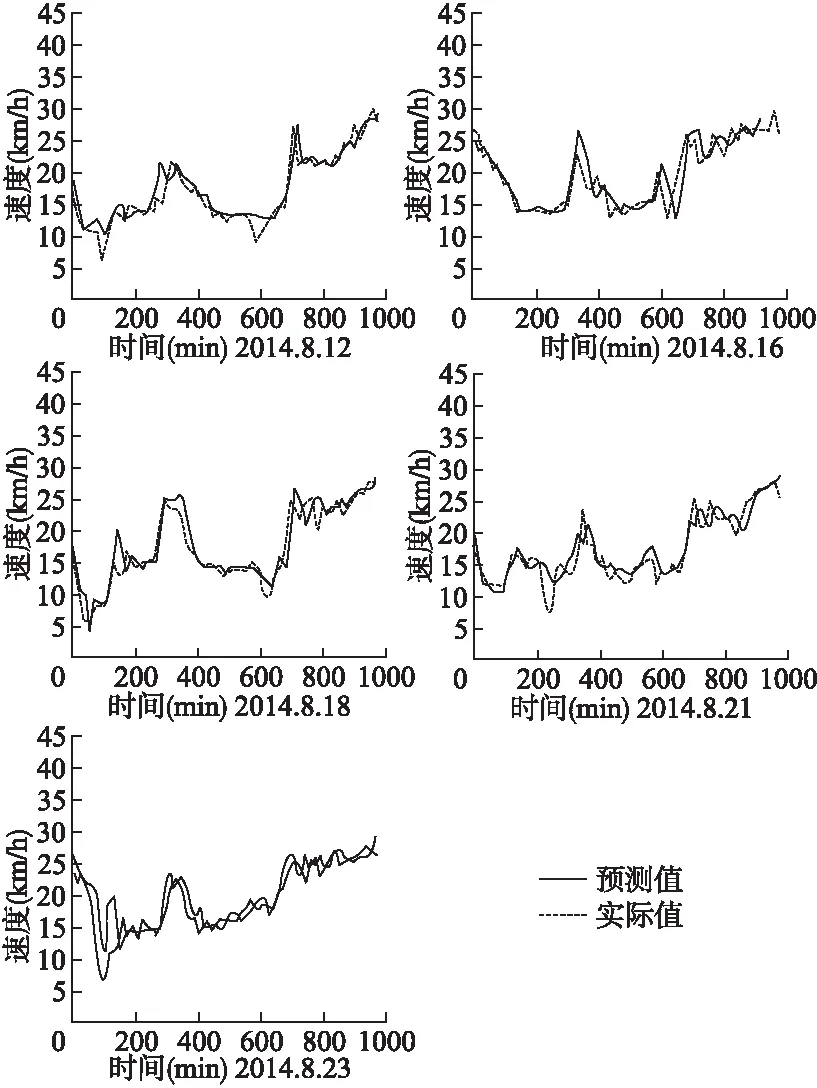
5.3 对比实验
Table 5 Prediction accuracy table for different methods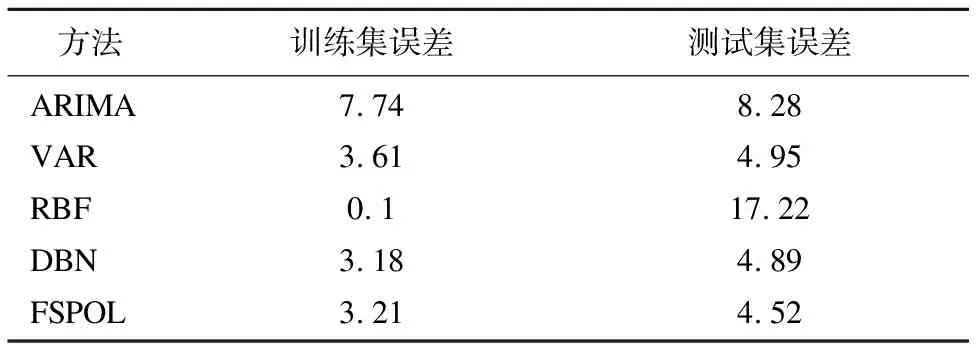
6 总 结
