基于Drucker-Prager模型的FRP约束混凝土力学性能分析

蔡小玲 杨俊杰

(1.无锡环境科学与工程研究中心,无锡 214153; 2.无锡城市职业技术学院建筑工程学院,无锡 214000;3.浙江工业大学建筑工程学院,杭州 310014)

0 引 言

纤维增强复合材料(Fiber Reinforced Polymer,FRP)具有强度高、质量轻和耐腐蚀等优点,并已经广泛应用于加固和新建结构中[1-4]。如果混凝土受到FRP布的约束,其抗压强度和延性将得到极大的提高。FRP约束实心混凝土目前已得到广泛的研究,我国规范[5]也对此类构件的设计作出了规定。关于FRP-混凝土-钢双壁柱(即FRP约束空心混凝土)的研究却相对缺乏。除强度高、延性好以外,该结构形式还具有自重轻和抗弯刚度大的优点,可以被用于桥梁和高层结构中。

文献[6-8]对FRP-混凝土-钢双壁短柱的轴压性能进行了实验研究并提出了应力-应变关系模型。研究表明:混凝土可以有效抑制内钢管的屈曲而内钢管可以为混凝土提供有效的约束。实验研究虽然可以准确的模拟实际情况,但是它不能够了解混凝土截面的应力分布也很难进行大量的参数分析。此外,已有的应力-应变模型基本都只适用于FRP约束实心混凝土,不能够考虑不均匀约束应力的影响。但是有限元模拟可以克服上述确定,尤其是能够得到混凝土截面的应力分布情况。有限元模拟采用的约束混凝土本构关系一般都来自Drucker-Prager模型或塑性损伤模型。研究人员对这些模型进行了适当的改进使之能够较好地模拟FRP约束混凝土的力学性能[9-10],但是此类研究仍较为缺乏或缺少足够的实验验证。

本文旨在通过基于Drucker-Prager材料模型的有限元方法对FRP约束混凝土,尤其是FRP-混凝土-钢双壁柱(FRP约束空心混凝土)的轴压力学性能进行研究。基于主动约束混凝土和FRP约束实心混凝土的实验研究,作者对有限元软件ABAQUS提供的线性Drucker-Prager材料模型进行了适当的改进,并通过实验数据验证了改进后材料模型的正确性。在此基础上,本文进行了广泛的参数分析,主要包括混凝土截面应力分布的比较、空心率和FRP约束刚度对FRP约束空心混凝土力学性能的影响。作者最后对此类FRP约束混凝土的极限强度和极限应变进行了预测并和已有的实验结果进行了比较。

1 Drucker-Prager材料模型及其改进

1.1 屈服准则

Drucker-Prager准则可以理解为von Mises准则的简单修正,它主要考虑了静水压力对屈服的影响。ABAQUS提供了三种扩展的Drucker-Prager模型,本文只讨论其中的线性模型。线性Drucker-Prager 模型屈服准则的数学表达式为

F=t-ptanβ-d=0

(1)

p=-I1/3

(2)

式中:t与偏应力张量的第二不变量(J2)和流动应力比值(K)相关;I1是主应力张量的第一不变量;β是材料的摩擦角;d是强化/软化函数。

系数K为等双轴抗压强度和三轴抗压强度的比值,其主要控制屈服面在偏平面上的形状。当K=1时,在偏平面上的屈服面为von Mises圆。根据文献[10]的研究,FRP约束混凝土的K值在0.7左右。为了确保屈服面外凸,ABAQUS将K的取值限定在0.778和1之间。若无特别说明,本文将K取为0.78。

本文基于FRP约束圆形混凝土的经验强度公式来推导材料摩擦角β的取值。混凝土在均匀环向压力(fl)下的轴压强度可由式(3)确定[11]:

(3)

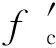
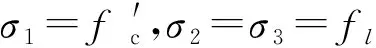
(4)

因为假定β只与材料本身有关而与σl无关,故可求得摩擦角β为53.7°。

1.2 强化准则

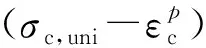
(5)

式中,β是1.1节中确定的摩擦角。

本节将通过文献的实验数据来推导适用于FRP约束混凝土的强化准则模型。

文献[13]对主动约束混凝土(均匀围压)和FRP约束混凝土的轴压性能进行了研究。混凝土试件为直径63 mm、高126 mm的圆柱体,其单轴抗压强度为51.6 MPa。主动约束混凝土承受的恒定围压分别为5 MPa、7.5 MPa、10 MPa、15 MPa、20 MPa和25 MPa。根据实验测定的轴向应力-应变曲线和所受的围压可以确定混凝土在整个加载过程中的应力状态和应变状态(主要是轴向塑性应变)。混凝土的轴向塑性应变可以由下式确定:

(6)

图1 硬化准则模型Fig.1 Strain hardening rule

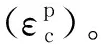
基于上述讨论,FRP约束混凝土的强化准则模型(即ABAQUS中输入的应力-塑性应变数据)为:达到峰值应力前与单轴受压混凝土的应力-塑性应变数据一致,此后应力保持恒定。若无单轴应力-应变的实验数据可根据我国混凝土规范[14]确定,并将总应变根据式(6)转换为塑性应变(σl=0)。

1.3 流动法则

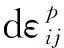
(7)

式中:dλ为非负标量函数;∂G/∂σij规定了塑性应变增量矢量的方向;G为塑性势能函数。

如果塑性势能函数和屈服函数F相同,则流动法则和屈服条件是关联的,反之则为非关联的。由于混凝土的复杂性,需采用非关联的流动法则。ABAQUS将塑性势能函数定义为[12]

G=t-ptanψ

(8)

式中:t,p的定义同式(1);ψ是膨胀角,材料膨胀时为正,收缩时为负。

研究表明[10],FRP约束混凝土的膨胀角在加载过程中不是恒定不变的而是和塑性应变有关。

(9)

λ1=11.61ρ+980

(10)

λ2=5 700ρ+225 000

(11)

ψu=101.66exp(-0.06ρ)-37.5

(12)

(13)

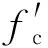
由式(9)可知,流动法则主要与FRP的约束刚度有关。

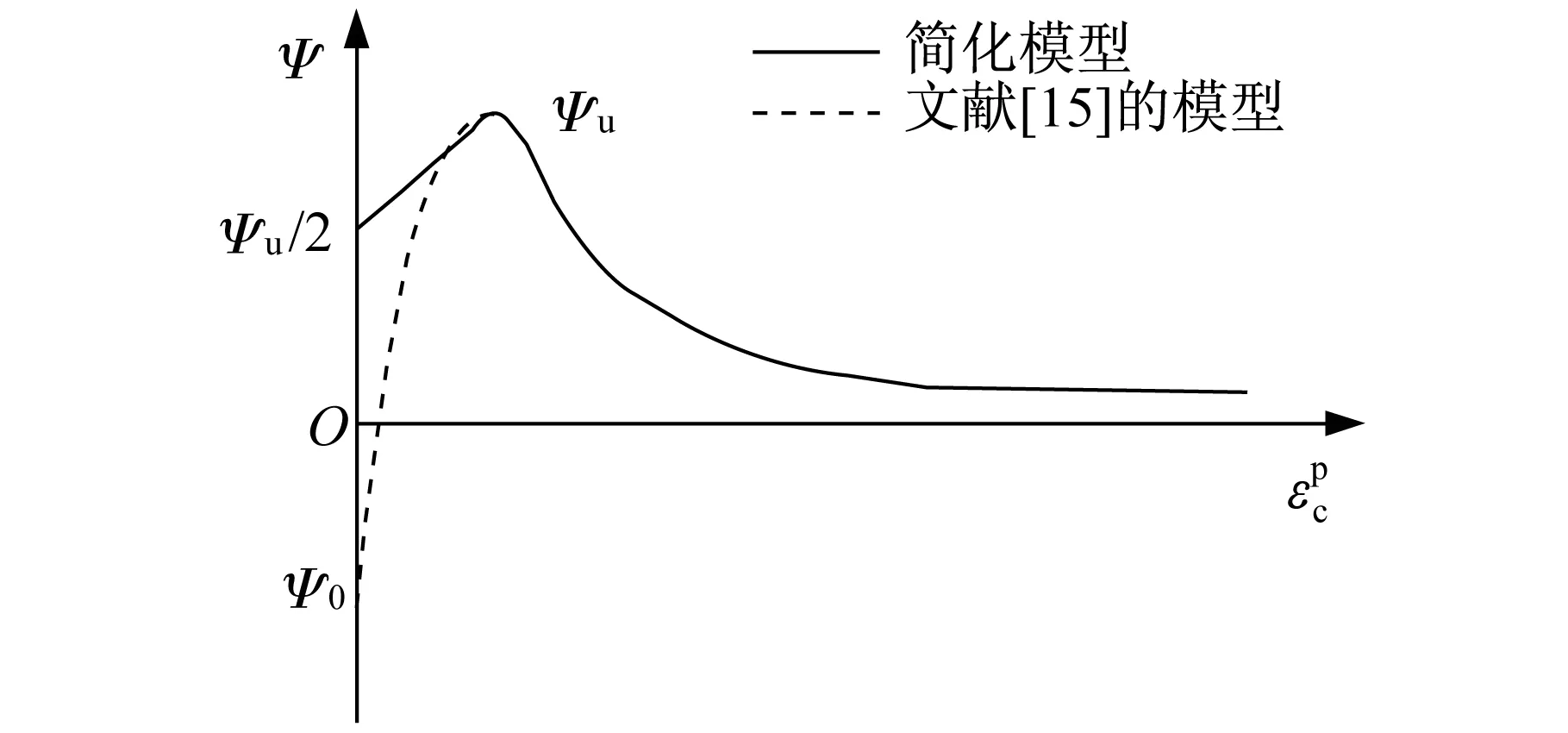
图2 流动法则Fig.2 Flow rule

1.4 Drucker-Prager模型在ABAQUS中的实现

有限元软件ABAQUS提供了线性Drucker-Prager材料模型来模拟约束混凝土的力学性能。摩擦角(friction angle,β=53.7°)、流动应力比(flow stress ratio,K=0.78)由第1.1节确定。强化模型数据(Drucker-Prager hardening data)由第1.2节提出的强化准则模型确定。以上的参数都与应变无关,在计算过程中保持不变。

根据第1.3节对流动法则的讨论,膨胀角(dilation angle =ψ)与混凝土的塑性应变相关,在计算过程中随着塑性应变的发展而变化。ABAQUS中的SDFV选项可以实现用户自定义与域变量(如塑性应变)相关的材料性质。该域变量又可以通过用户子程序(subroutine)来定义。通过此方法可以考虑膨胀角在计算过程中随着塑性应变发展的变化。

2 模型验证

2.1 FRP约束实心混凝土

文献[13]共对6类18个FRP约束混凝土圆柱体进行了轴向压缩试验。试件共包括三类FRP(表1)和两种厚度(一层或两层),其中,t是每层FRP布厚度,fuh是FRP抗拉强度,Ef是FRP弹性模量。混凝土圆柱体的尺寸仍为半径63 mm、高126 mm。素混凝土单轴抗压强度为51.6 MPa。

表1FRP材性

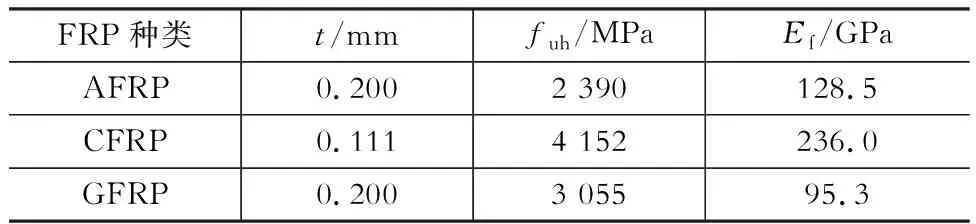
Table 1Material properties of FRP

基于ABAQUS的有限元模型如图3所示。由于对称性,本文只对实际试件的1/8建模。FRP布采用膜单元(M3D4R),混凝土采用实体单元(C3D8R)。模型底面(即实际构件的中间截面)的Z方向平动,侧面1的Y方向平动和侧面2的X方向平动被约束。模型采用位移加载,在其顶面添加一个竖直向下(-z方向)的位移。模型的网格划分如图3所示,单元尺寸大致为2 mm×2 mm。FRP布和混凝土界面部分的节点自由度彼此耦合(ABAQUS中的“Tie”命令),即FRP布和混凝土无相对滑动。FRP布设为各项异性材料,只考虑其环向模量,纵向模量、剪切模量设为无限小,泊松比为零。混凝土采用线性的Drucker-Prager材料模型,其参数设置(即屈服准则,强化准则和流动法则)根据本文第1节中的相关推导确定。因为模型上下端面的Ux和Uy自由度均未约束,构件不存在端部约束效应。截面应力分布沿z向无变化,文中选取模型的底面(即实际构件的中部截面)进行截面应力分析。

由图4所示的应力-应变曲线可知:基于Drucker-Prager材料模型的有限元模型可以较准确地预测FRP约束实心混凝土在轴向压缩时的应力、应变发展过程,混凝土的极限状态应力也可以得到准确地预测。

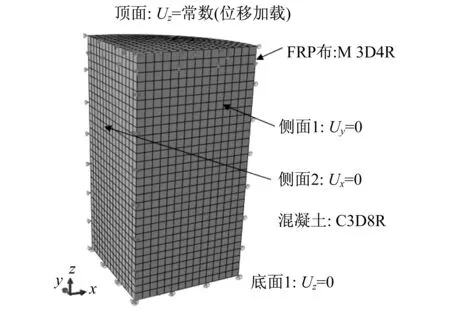
图3 FRP约束混凝土有限元模型Fig.3 FEM model of FRP confined concrete

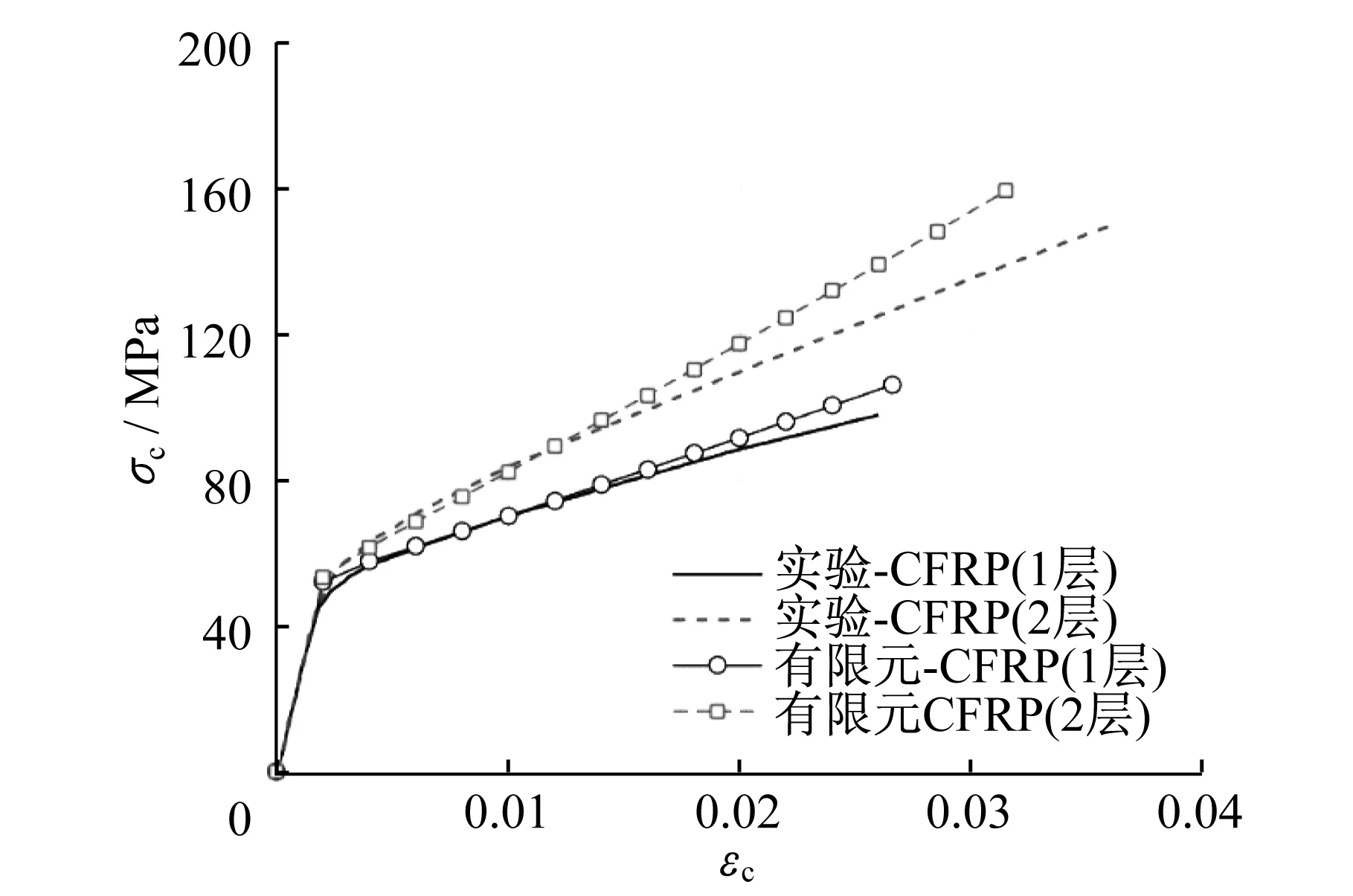
图4 FRP约束混凝土的应力-应变曲线Fig.4 Stress-strain curves of FRP confined concrete

2.2 FRP约束空心混凝土

较之FRP约束实心混凝土(图5(a)),FRP约束空心混凝土具有自重轻、抗弯刚度大等优点。此外,空心混凝土收到不均匀的约束应力,其横截面的轴向应力分布也是不均匀(详见第2.1节的讨论),只有通过有限元分析才能准确地确定其横截面的应力分布。本文选取了文献[8]的实验结果来验证有限元模型。实验试件的截面形式如图5(b)、图5(c)所示,二者的唯一区别是有无内钢管。

用于验证的试件分别是DSTC(D37-C2-I,II)和CFHT(H37-A2-I,II)。FRP布的弹性模量是80.1GPa,拉伸强度为1 060.6 MPa(已考虑强度折减系数0.581,详见文献[16]),厚度为0.34 mm。素混凝土单轴抗压强度为37 MPa。混凝土外径为152.5 mm,DSTC试件的内径为88 mm (钢管壁厚2.1 mm,屈服强度352.7 MPa),CFHT试件的内径为42 mm。基于ABAQUS的有限元模型和第2.2节中的类似,内钢管采用理想弹塑性模型,其单元类型为壳单元S4R。内钢管和混凝土内壁的界面节点的自由度仍全部耦合。

实验得到的和有限元分析得到的应力-应变曲线的比较如图6所示。本文提出的有限元模型可以较准确地预测FRP约束空心混凝土的应力-应变曲线。极限应力预测误差在10%以内,能够满足精度要求。通过本节的验证可以表明,基于Drucker-Prager材料模型的有限元模型可以合理地预测FRP约束混凝土的力学性能,该模型能够用于后续的参数分析。

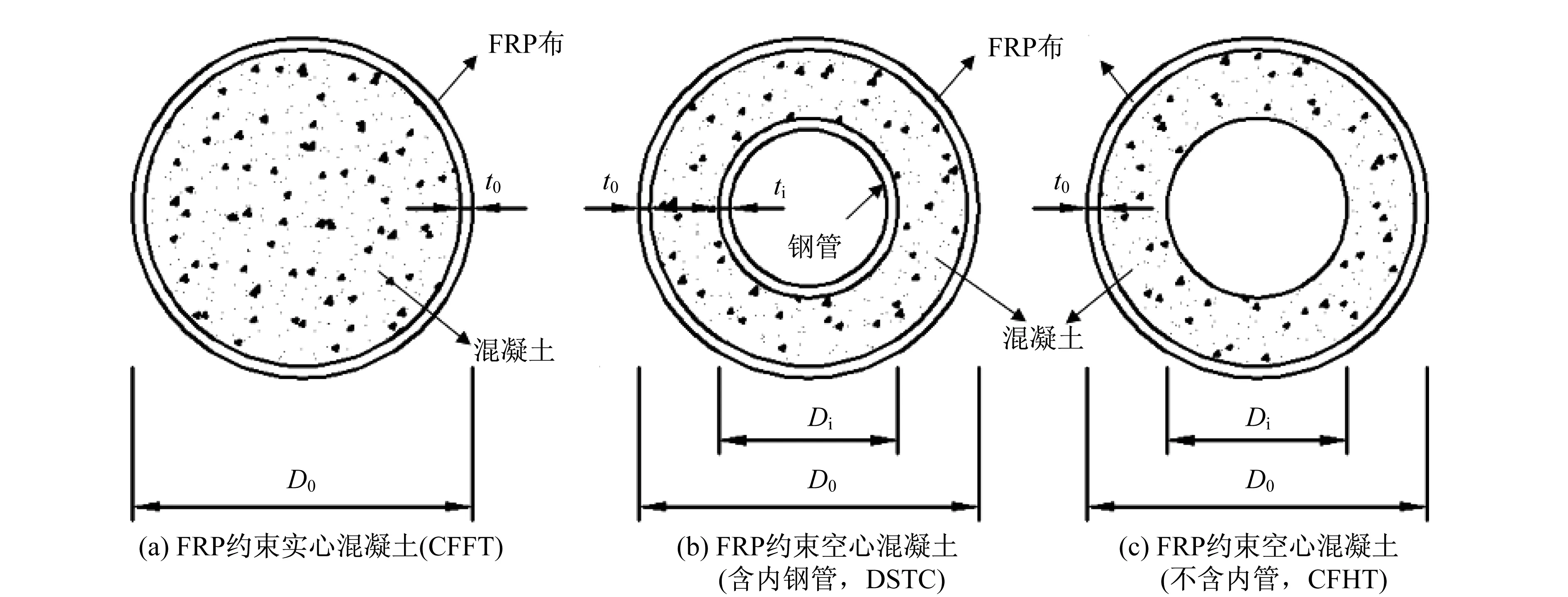
图5 截面形式Fig.5 Cross-section type

图6 FRP约束空心混凝土的应力-应变曲线Fig.6 Stress-strain curves of concrete-filled double-skin tubes

3 参数分析

3.1 混凝土截面应力分布

本小节主要研究了FRP约束实心混凝土(CFFT,图5(a))和FRP约束空心混凝土(含内钢管,DSTC图5(b);不含内钢管,CFHT图5(c))的截面应力分布。试件的几何尺寸为:外径150 mm,

内径80 mm,FRP布厚度0.3 mm,内钢管厚度2.0 mm。混凝土单轴抗压强度为51.6 MPa,钢管的屈服强度为300 MPa。FRP布弹性模型为200 GPa,抗拉强度为1 630 MPa。有限元模型的建立和分析过程同本文第2节的介绍。达到极限状态时的混凝土截面应力云图如图7所示,其中受压为负,s11表示径向应力,s22表示环向应力,s33表示轴向应力。

对于FRP约束实心混凝土(图7(a)),由于混凝土受到均匀的约束,其环向和径向应力的大小相等(均等于约束应力fl),轴向应力也在截面上均匀分布。轴向应力和环向、径向应力的关系完全满足式(3)。然而,对于FRP约束空心混凝土(图7(b)、图7(c)),其截面上的应力分布是不均匀的。环向应力和轴向应力的大小均沿着径向(由内到外)降低,而径向应力的大小沿着径向增加。这些应力沿着环向均是均匀分布的。图7也表明由于应力分布的不均匀,式(3)不能直接使用以确定轴向应力和约束应力的关系。

图7 FRP约束混凝土截面应力分布Fig.7 Cross-sectional stress distribution of FRP confined concrete

为了进一步分析FRP约束空心混凝土的截面应力,图8绘出了径向应力(σr=s11)和环向应力(σθ=s22)沿径向的变化,其中,p0为约束应力。图8表明径向应力沿着径向增加(均小于约束应力),环向应力沿着径向降低(均大于约束应力),且在任意位置的环向应力均大于径向应力。对于FRP约束实心混凝土,其径向和环向应力均等于约束应力。图8绘出了含内钢管(DSTC)和不含内管(CFHT)两种情况下的混凝土截面应力分布。若增加内钢管,径向应力值会提高而环向应力值会降低,混凝土圆环内侧和外侧的应力梯度会降低(即截面的径向和环向应力分布趋于均匀)。由图8的轴向应力云图可知,内钢管可以使截面轴向应力的分布更加均匀,但是其外侧的轴向应力会略低于不含内钢管的FRP约束混凝土。图8中的虚线为根据弹性力学计算所得的应力分布(无内钢管),可以发现有限元计算结果和理论分析结果基本一致。

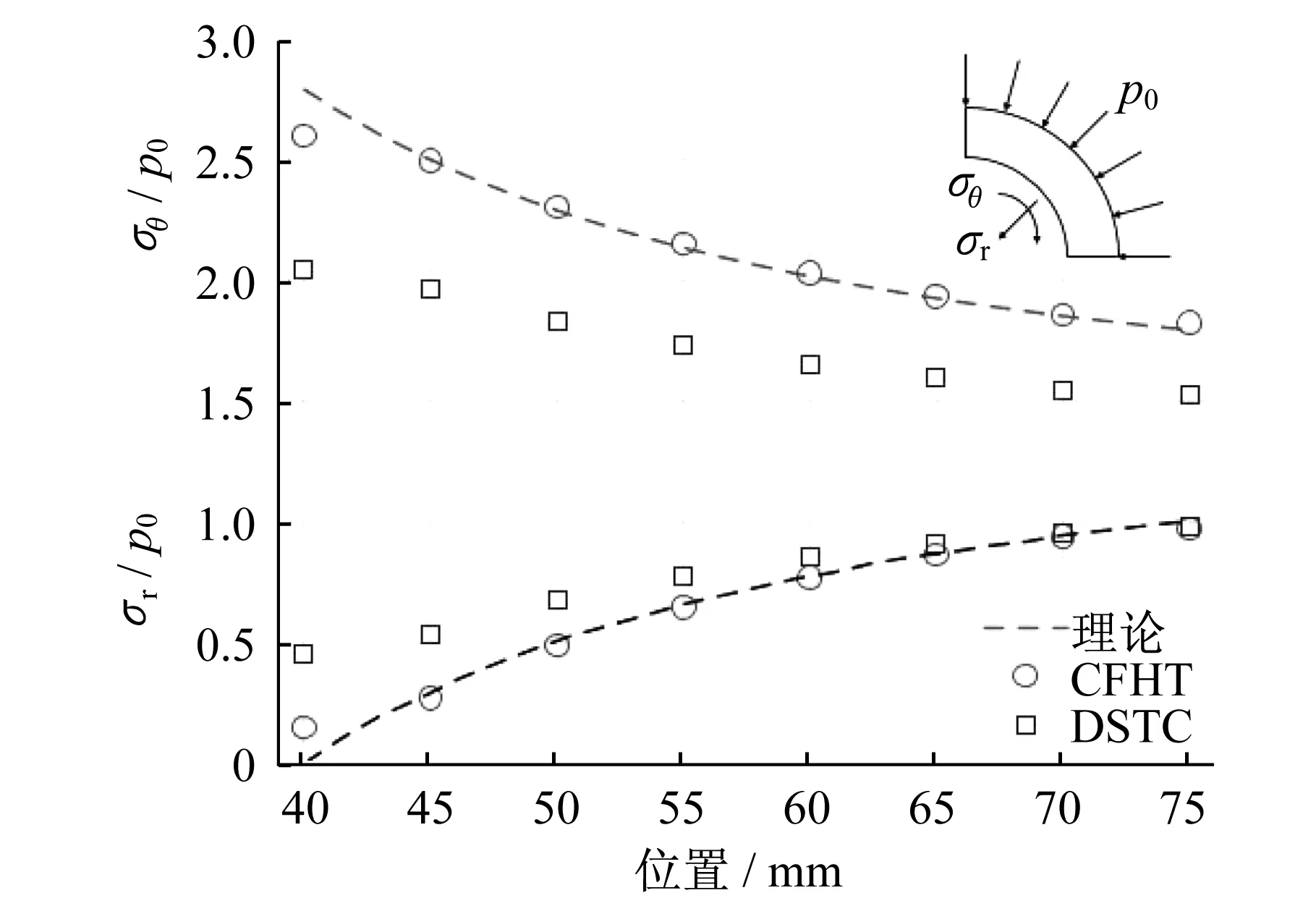
图8 径向和环向应力沿径向的分布Fig.8 Radial and circumferential stress distribution along radial direction

3.2 空心率的影响

由第3.1节的讨论可知,内钢管可以显著降低混凝土截面应力分布的不均匀性。实验研究[8]也表明,若无内钢管,内侧混凝土更易被压坏且混凝土向内的膨胀不能被有效的约束,进而降低了FRP的约束效应。因此无内钢管的FRP约束混凝土(CFHT)在工程实际中的应用价值不大,本文接下来将只对含内钢管的FRP约束空心混凝土(DSTC,即FRP-混凝土-钢双壁短柱)的力学性能进行讨论。

空心率(φ)是影响FRP约束空心混凝土力学性能的重要因素。空心率的定义为混凝土圆环内径和外径之比。本文选取了四个空心率进行分析(即φ=0,0.27,0.53和0.80),分别对应实心混凝土,内径为40 mm、80 mm和120 mm的空心混凝土试件。除FRP布的抗拉强度设为1 500 MPa外,试件的其他参数同第3.1节。有限元分析所得的应力-轴向应变曲线和横向-轴向应变曲线如图9所示。随着空心率的增加,这些曲线的形状并没有明显的改变。如图9所示,混凝土的极限强度和极限轴向应变都随着空心率的增加而增加。FRP约束空心混凝土比实心混凝土具有更高的强度和更好的延性。

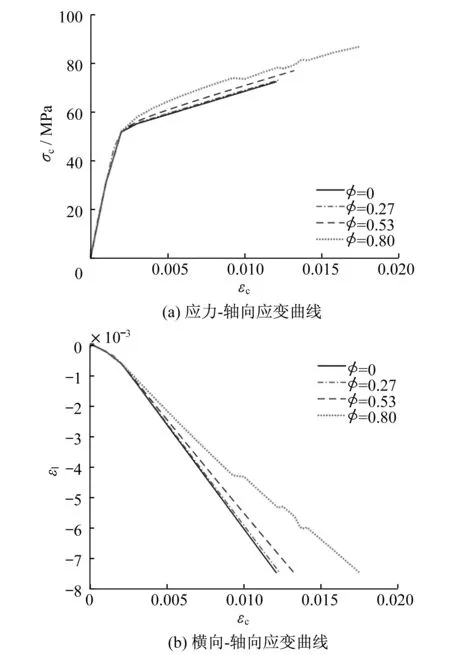
图9 空心率对FRP约束空心混凝土(DSTC)性能的影响Fig.9 Effects of void ratio on behaviour of concrete-filled FRP double-skin tubes (DSTC)

3.3 FRP约束刚度的影响

混凝土的三轴抗压强度与其所受的围压直接相关。对于FRP约束混凝土,FRP布的刚度决定了围压增长的快慢和围压的大小(若假定FRP布极限拉伸应变不变)。因此FRP约束刚度对混凝土的力学性能有较大的影响。本文采用约束刚度系数(ρK)来表征FRP布的约束刚度,其定义如下[17]:

(14)

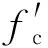
本小节分析了不同约束刚度系数下的混凝土应力-应变曲线和横向-轴向应变曲线。约束刚度系数分别为0.21、0.31、0.41、0.62和0.83,分别对应的FRP布厚度为0.2 mm、0.3 mm、0.4 mm、0.6 mm和0.8 mm。试件的其他参数同第2.2节。

图10给出了不同约束刚度下的FRP约束空心混凝土的应力-应变曲线和横向-轴向应变曲线。随着约束刚度的增加,应力-应变曲线的强化阶段曲线的斜率有明显的增加,这表明混凝土轴压应力增加的速率提高了。约束混凝土的极限强度和极限轴向应变也随着约束刚度的增加而增加,但是约束刚度对极限强度的影响更为明显。比较图9和图10可知,空心率对轴向应变的影响更为明显,而约束刚度对轴压强度的影响更为明显。

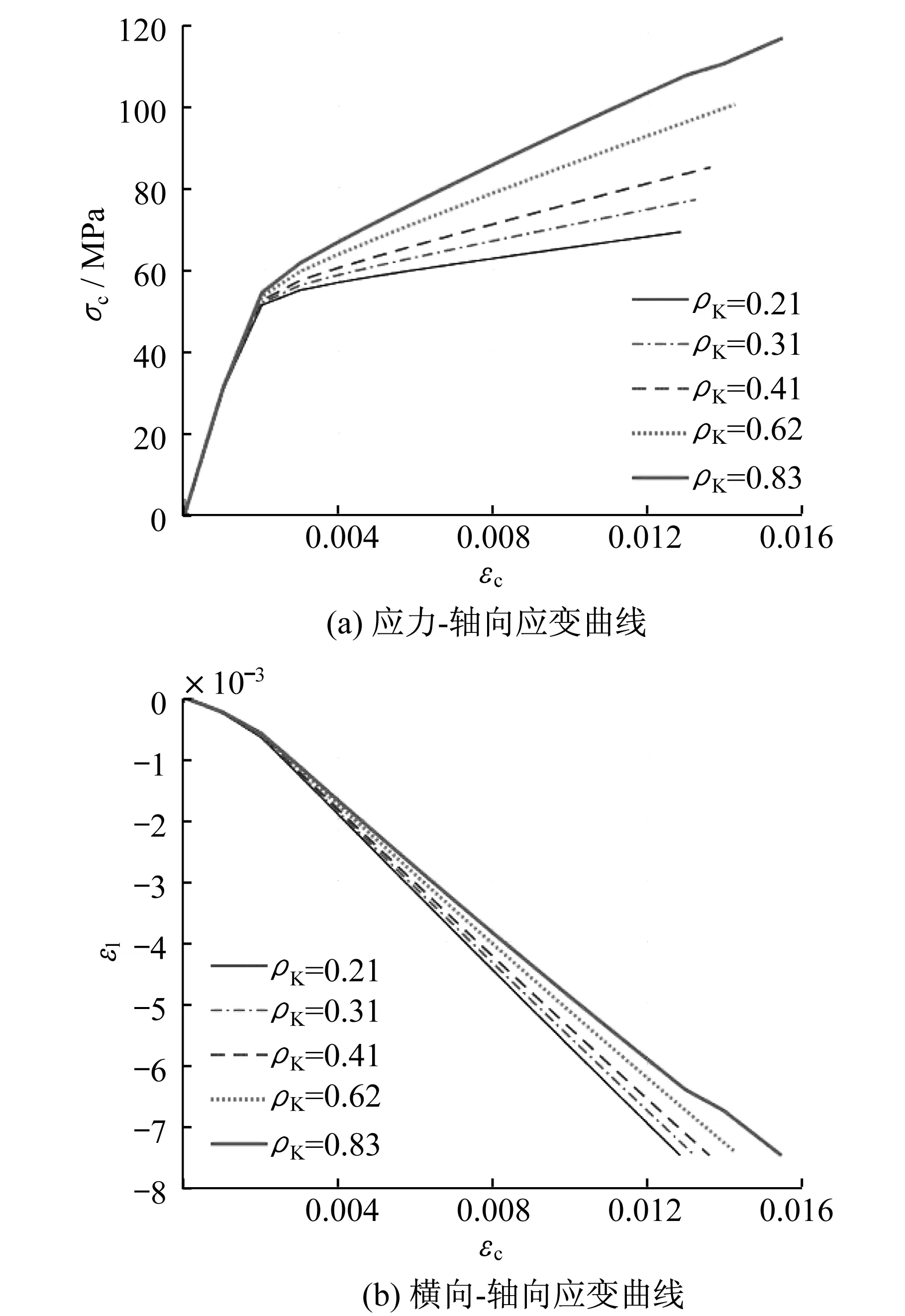
图10 约束刚度对FRP约束空心混凝土(DSTC)性能的影响Fig.10 Effects of confining stiffness ratio on behaviour of concrete-filled FRP double-skin tubes (DSTC)

4 极限强度预测

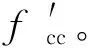
(15)

(16)

式中:fuh是FRP布抗拉强度;系数ke只与空心率相关,二者的关系通过拟合本文3.2节的有限元结果确定:

(17)

基于上述方法,FRP约束空心混凝土的极限状态预测如图11所示,其中包括了文献[7-8]的实验结果。由图11可知,式(15)-式(17)可以较准确地预测混凝土的极限强度,预测结果和有限元(或实验)结果之比的平均值为1.01,变异系数为0.10。

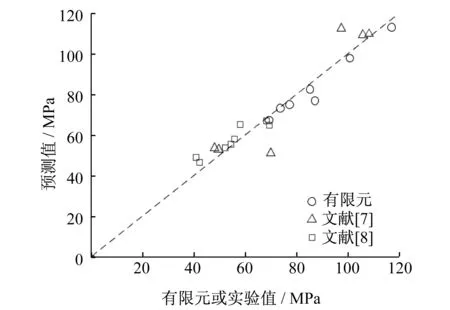
图11 FRP约束空心混凝土(DSTC)的极限强度预测Fig.11 Prediction for ultimate strength of concrete-filled FRP double-skin tubes (DSTCs)

5 结 论

本文基于Drucker-Prager模型运用有限元软件ABAQUS对FRP约束混凝土的力学性能进行了研究,可以得到以下主要结论:

(1) 对于ABAQUS自带的线性Drucker-Prager模型,FRP约束混凝土的摩擦角为53.7°。用于强化准则模型的应力-塑性应变数据为:达到峰值应力前与单轴受压混凝土的一致,此后应力保持恒定。流动法则可以根据式(9)确定。通过实验验证,本文确定的Drucker-Prager模型的参数能够满足精度要求。

(2) 与FRP约束实心混凝土相比,约束空心混凝土的截面应力(径向、环向和轴向应力)分布并不均匀。通过设置内钢管可以降低应力分布的不均匀性,改善FRP约束空心混凝土的力学性能。

(3) 本文讨论了空心率和FRP约束刚度对FRP约束空心混凝土(含内钢管,DSTC)力学性能的影响。空心率增加和FRP约束刚度的增加均可导致混凝土极限强度和极限应变的增加。研究发现,空心率对极限应变、约束刚度对极限强度的影响更为明显。

(4) 本文提出了对FRP约束空心混凝土极限强度的预测公式,该公式考虑了空心率的影响,并和有限元结果及实验结果的误差很小。