压弯Π形梁剪力滞的数值解法
2019-01-23周世军
周世军 宋 刚
(1.重庆大学土木工程学院,重庆 400045; 2.重庆大学山地城镇建设与新技术教育部重点实验室,重庆 400045;3.贵州省交通规划勘察设计研究院股份有限公司,贵阳 550081)
0 引 言
Π形梁具有自重轻、桥面宽等特点,广泛应用于新建桥梁,特别是斜拉桥。因为Π形梁的建造过程中常伴有轴向压力作用,同时桥面过宽剪力滞效应突出,故有必要研究在压弯作用下Π形梁的剪力滞计算方法。
在剪力滞的数值解法上,Luo[1]、张元海等[2-3]相继在能量变分法[4]的基础上,针对一维梁段有限元进行了大量的研究与改进,但主要集中在箱形截面,对Π形梁的讨论尚不充分。在剪力滞的解析理论方面,Chen等[5]近来针对矩形箱梁提出了一种无须假设剪力滞翘曲位移模式的剪力滞闭合解法,但并不适于压弯Π形梁。
针对截面纵向位移模式的研究,Zhang[6-7]、周茂定[8]基于面内剪切变形和截面应力轴向平衡条件,对截面纵向位移函数进行了轴向修正;Lin等[9]提出了一种具有轴向位移修正和高阶剪滞翘曲位移的截面纵向位移函数,但上述的轴向位移修正项均不独立,无法应用于具有轴向自由度的压弯构件。Zhu和Nie[10-11]基于Dezi等[12-13]提出的二次剪滞翘曲位移,对Π形组合梁也提出了一种考虑轴向位移的剪力滞解析模型,但却未能给出其闭合解。
在压弯作用下,程翔云等[14]通过引入梁柱效应与纵向位移差分别研究压弯和轴压作用下箱梁的剪力滞效应;Chang[15]、Zhou[16-17]和蔺鹏臻等[18]先后对预应力混凝土箱梁的剪力滞效应进行了研究;李乔、万臻[19-20]以及张永健等[21]对斜拉桥中Π形主梁的剪力滞进行了试验分析。现有研究多采用板壳、实体有限元的数值方法[22-23],或模型试验与现场实测[20,23],理论研究尚显不足。
Π形梁剪力滞效应的现有成果往往仅关注弯曲作用下的剪力滞,对有轴向力的主梁(如斜拉桥),分析多局限于对轴力工况的单独分析,未能将轴向位移作为独立自由度考虑,从而不能合理分析压弯作用下Π形梁的剪力滞效应。本文针对压弯Π形梁的剪力滞效应,引入独立的轴向位移以合理描述压弯Π形梁截面纵向位移状态,并提出一种每节点4个自由度的一维有限梁段法,能有效解决各种边界条件下压弯Π形梁剪力滞效应的分析。
1 基本假定
针对剪力滞翘曲位移函数,文献[6]论证了弯曲作用下面内剪切变形使顶板纵向位移沿其板宽方向按二次抛物线分布;文献[14]同样也采用二次抛物线作为轴力作用下剪力滞的翘曲位移模式。由于轴力和弯曲均会产生剪力滞效应,本文假设其翘曲位移模式均为二次抛物线,并将两者产生的剪力滞效应合并,用一个剪力滞位移表征压弯作用下的剪力滞。
图1所示的4个位移变量分别为z=0处腹板的轴向位移u(x)、截面竖向位移v(x)、截面转角θ(x)和剪切转角最大差值φ(x)(即压弯作用下的剪力滞位移)。
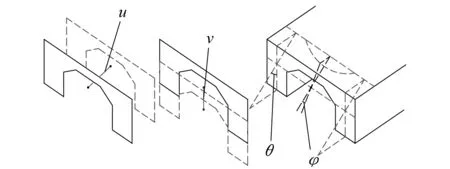
图1 Π形梁节点位移Fig.1Nodal displacementsof Π shaped girder
坐标系的建立如图2所示,位移方向的约定为:u(x)沿+x为正;v(x)沿+z为正;θ(x)和φ(x)绕+y旋转为正。
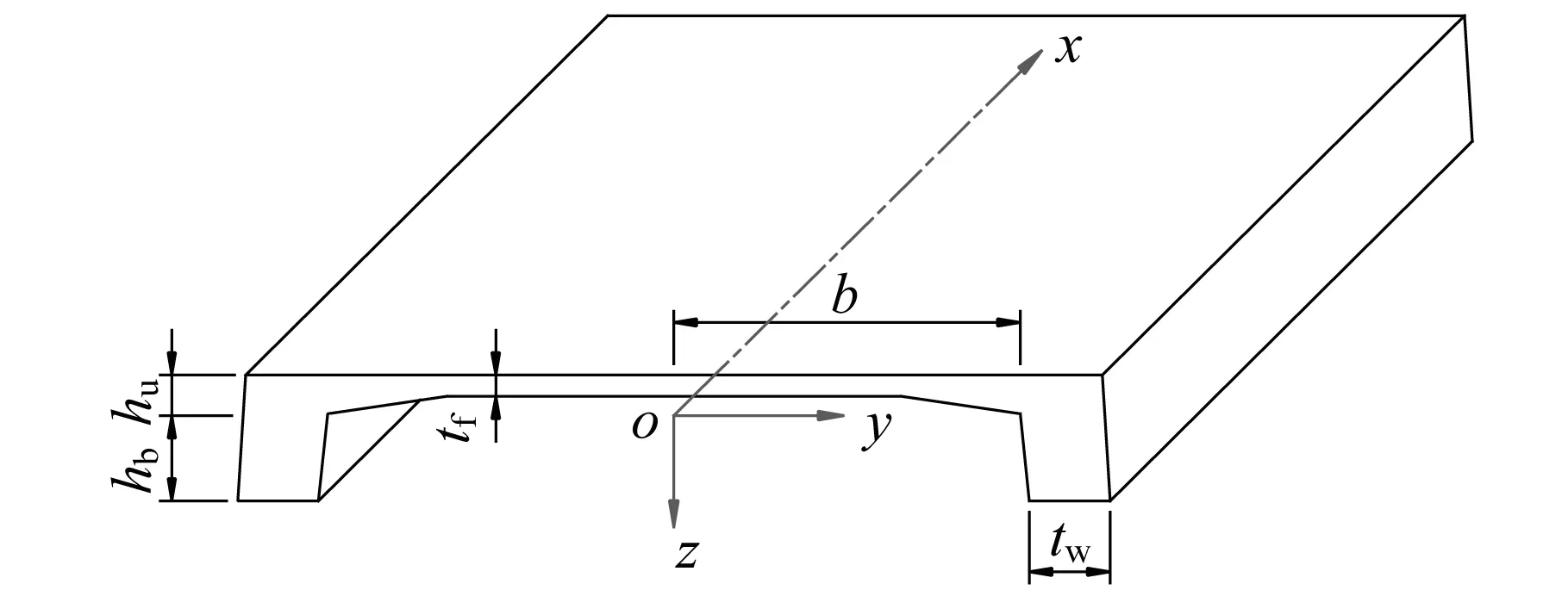
图2 Π形梁横截面与坐标系Fig.2 Cross section of Π shaped girder and coordinate system
引入轴向位移u(x)以合理描述压弯Π形梁截面纵向位移,具体为
(1)
式中:uf(x,y,z)为顶板纵向位移函数;uw(x,z)为腹板纵向位移函数;b为顶板宽度的1/2。
腹板仍满足平截面假定;对顶板而言,板内纵向纤维的竖向挤压变形、板平面外的剪切变形及横向弯曲、横向应变均属微量,忽略不计。
2 控制微分方程的建立
当主梁受到图3所示的外力荷载(图中荷载方向假定为正)时,主梁的总势能为:
(2)
式中:E为弹性模量;G为剪切模量;A为横截面面积;I为截面对y轴的惯性矩;If为顶板对y轴的惯性矩;Sf为顶板对y轴的面积矩;Iφ=8If/15;qv(x)为竖向分布荷载;qu(x)为轴向分布荷载;l为梁体长度;δe和fe为梁端位移及其相应的梁端荷载:
(3)
式中,N(x)为轴力;Q(x)为剪力;M(x)为弯矩;S(x)为与φ(x)对应的剪力滞矩。

图3 荷载图示Fig.3 Load diagram
对式(2)求变分,得
(4)
式(4)即为分析压弯Π形梁剪力滞效应的控制微分方程组。显然,位移u(x)、v(x)、φ(x)之间相互耦合。
令
(5)
当qv(x)=qv,qu(x)=qux+q0时,式(4)的通解为
(6)
式中,c1~c8为积分常数,式(6)对应的边界条件为
(7)
3 有限梁段法
如图1在每个节点引入4个节点位移,对式(6)进行离散化,并代入式(7)建立Π形梁单元节点位移与节点力间的对应关系,δe和fe重写为
(8)
式中:ui,j为节点轴向位移;vi,j为节点竖向位移;θi,j为节点转角;φi,j为节点剪力滞位移;Ni,j为节点轴力;Qi,j为节点剪力;Mi,j为节点弯矩;Si,j为节点剪力滞矩;节点上各物理量均以坐标轴正向为正,如图4所示。
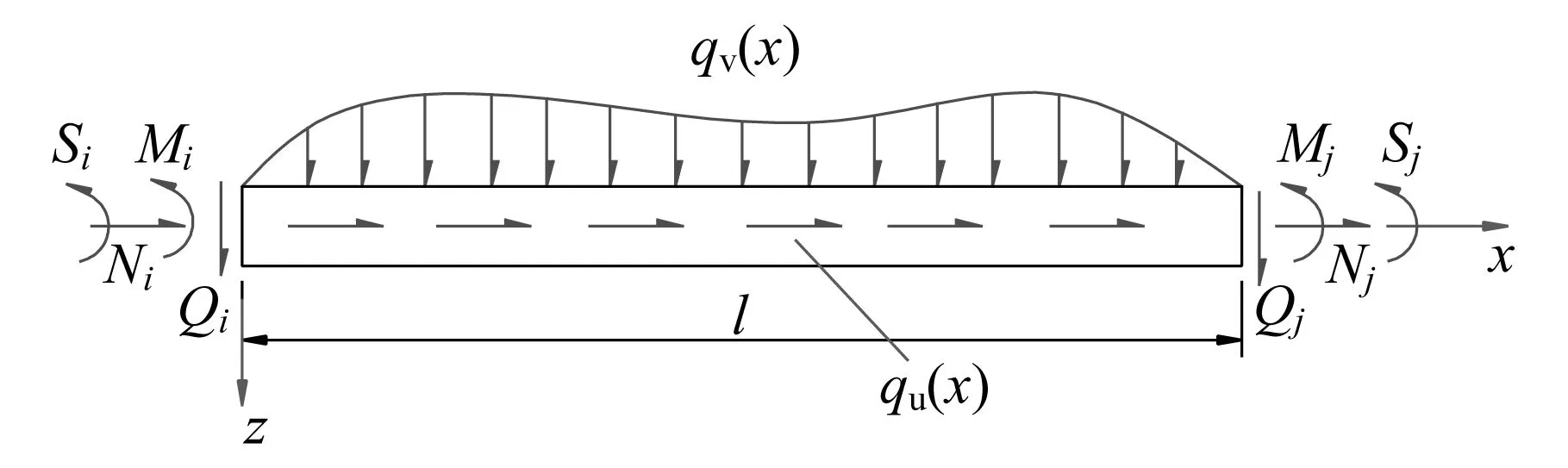
图4 节点力正方约定Fig.4 Nodal forces positive convention
根据式(6)~式(8),可得节点位移δe和节点力fe与积分常数c1~c8之间的关系式为
(9)
式中:C=(c1c2c3c4c5c6c7c8)T;Mδ,Mf分别为联系δe,fe与C的系数矩阵(8×8)。
令
(10)
将式(9)化为
(11)
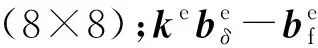
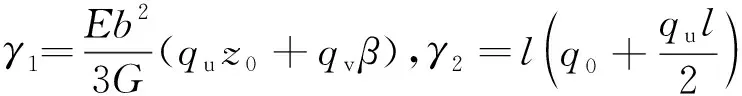
(12)
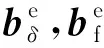
(13)
(14)
令
单元刚度矩阵ke中各上三角元素表示如下:
如图5所示为考虑剪力滞的压弯Π形梁单元刚度矩阵,节点剪力滞位移φi,j分别与节点轴向位移ui,j、节点竖向位移vi,j和节点转角位移θi,j相互耦合,与式(10)对应的坐标变换矩阵为:

(15)
式中,C=cosα,S=sinα,α为单元坐标系与结构坐标系间的夹角,规定由结构坐标系逆时针转到单元坐标系为正。

图5 单元刚度矩阵示意图Fig.5 Element stiffness matrixdiagram
4 算 例
结合图6所示的主梁断面尺寸,分别采用本文方法和ANSYS实体单元SOLID185分析简支梁、悬臂梁和连续梁在轴向压力Nx=500 kN和竖向均布荷载qv(x)=450 kN/m共同作用下的剪力滞效应。其中,材料的弹性模量E=3.55×107kN/m2,剪切模量G=0.4E。为实现实体单元与本文方法之间的比较,选择图6中的A点(腹板中面z=0处)作为实体单元响应输出位置,以保证两种计算方法之间的可比性。
如图7所示,在压弯作用下,本文方法与实体单元的位移分析结果吻合良好,能够正确反映轴向位移和竖向位移沿梁长的变化规律。对简支梁而言,轴向位移为负,沿轴力方向;对悬臂梁而言,轴向位移先正后负,固定端沿轴力反向,自由端沿轴力方向;对连续梁而言,轴向位移基本变化规律与简支梁相同,但在中间铰支座处轴向位移出现跳跃现象,跳跃方向沿轴力反向。由此表明,在压弯作用下,由于剪力滞效应的影响梁单元的轴向位移沿梁长的变化规律并非直线u(x)=Nxx/EA,而是随不同的受力状态和边界条件改变。

图6 横断面尺寸(单位:cm)Fig.6 Dimension of cross section (Unit:cm)
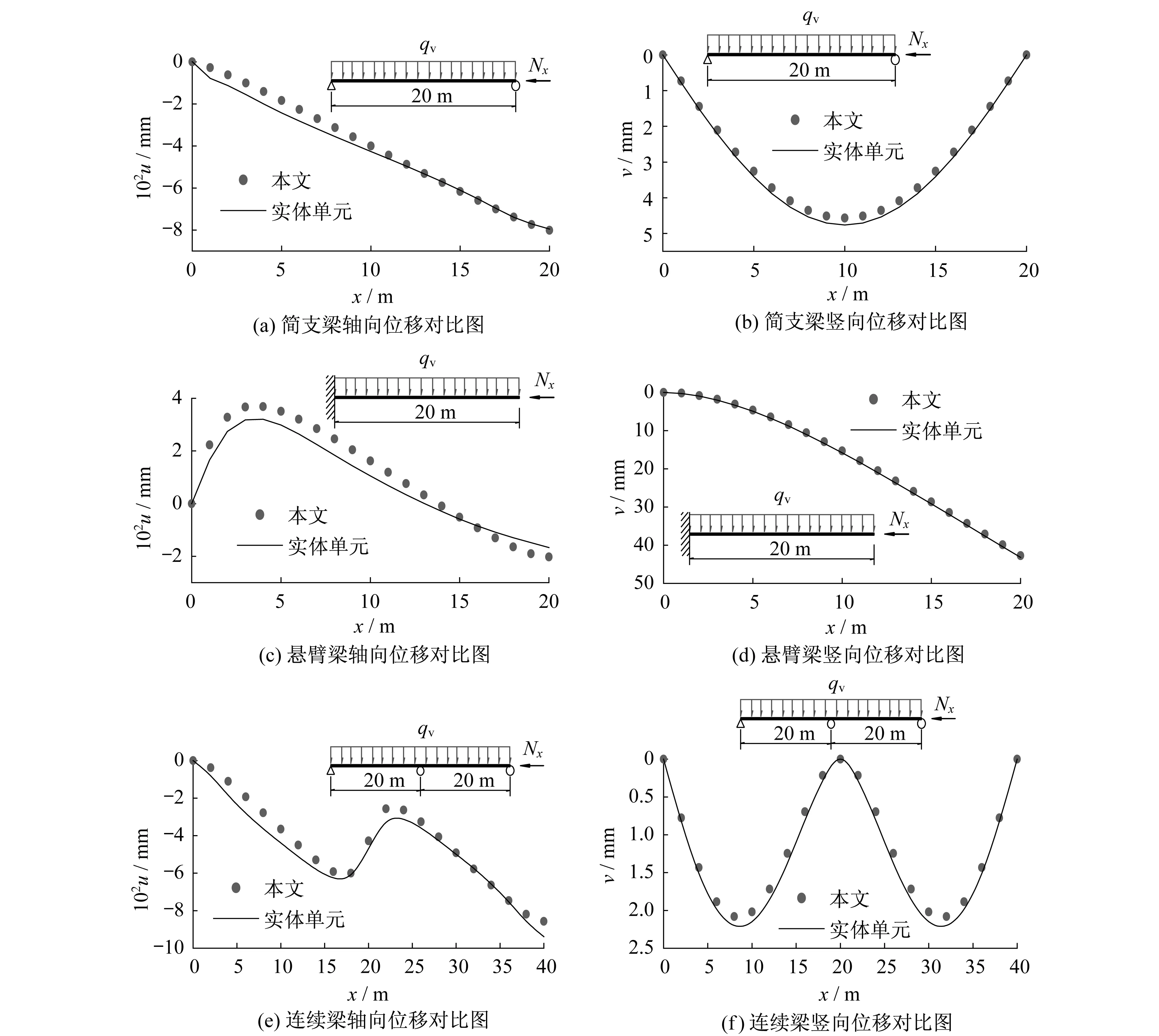
图7 压弯作用下实体单元和本文方法的位移对比图Fig.7 Displacement comparisons of solid elementandpresent methodunder axial compression and bending
结合式(1)和式(7),消去位移变量,得到顶板正应力σf与单元杆端力间的关系如式(16)所示。
(16)
如图8-图13所示,分别为Π形截面简支梁、悬臂梁和连续梁的广义力矩图,以及各主梁跨中截面顶板正应力分布图。经实体单元SOLID185验证,本文所提出的梁单元能够较准确地计算压弯Π形梁的截面正应力,合理反映了由剪力滞所引起的截面正应力分布不均匀的现象。同时,与文献[2]分析结果类似,在压弯作用下,Π形梁的剪力滞矩S和弯矩M同样也具有相似的分布规律,但相对于箱梁而言,Π形梁的剪力滞矩S的绝对值远小于弯矩M的绝对值,且轴向压力对广义力矩的影响极小,可忽略不计。

图8 简支梁的广义力矩图Fig.8 Generalized moment of simply supported girder
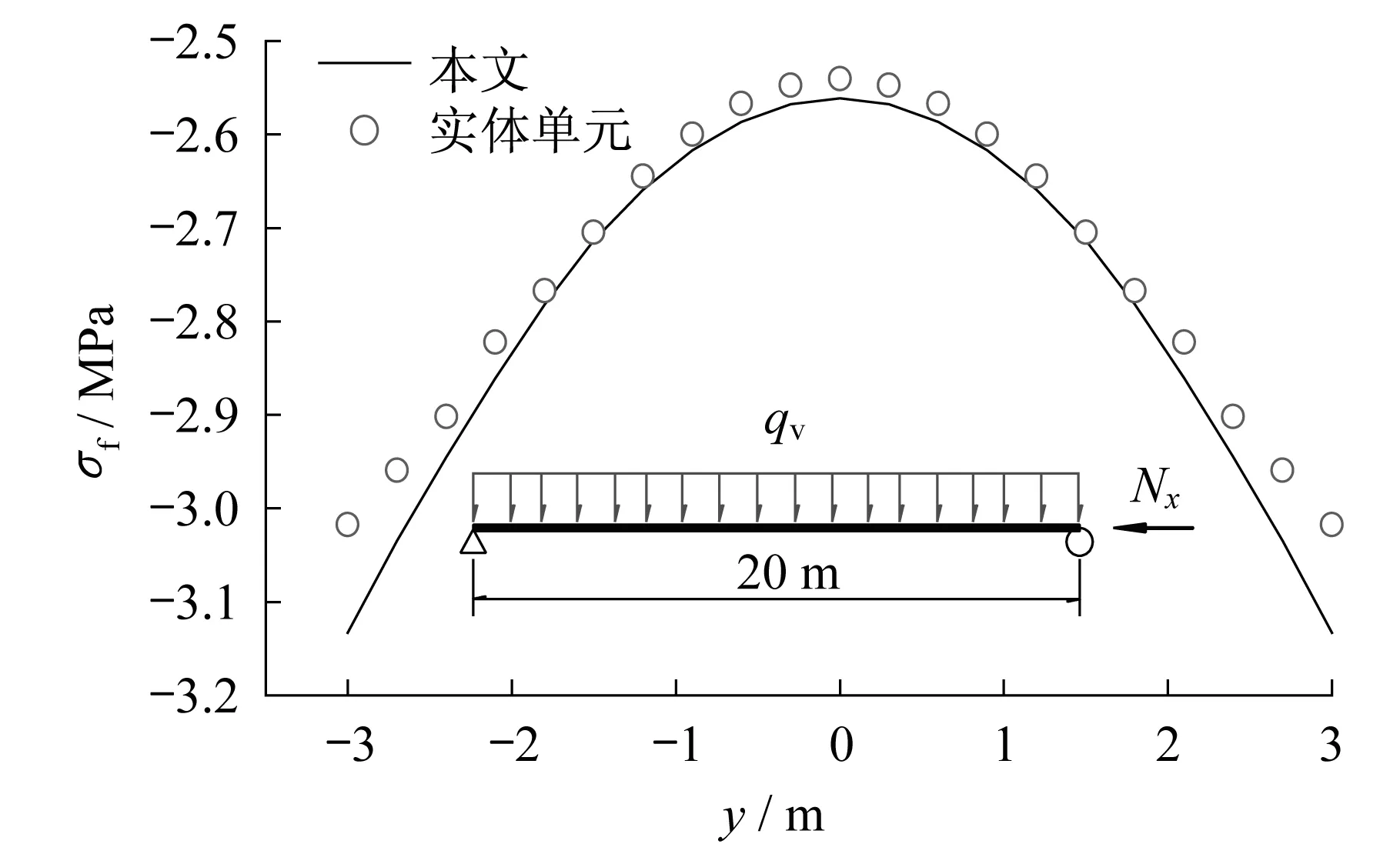
图9 简支梁跨中截面应力Fig.9 Stress on midspan section of simply supported girder
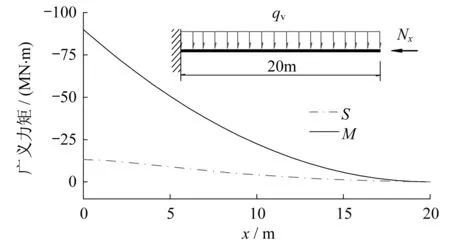
图10 悬臂梁的广义力矩图Fig.10 Generalized moment of cantilever girder
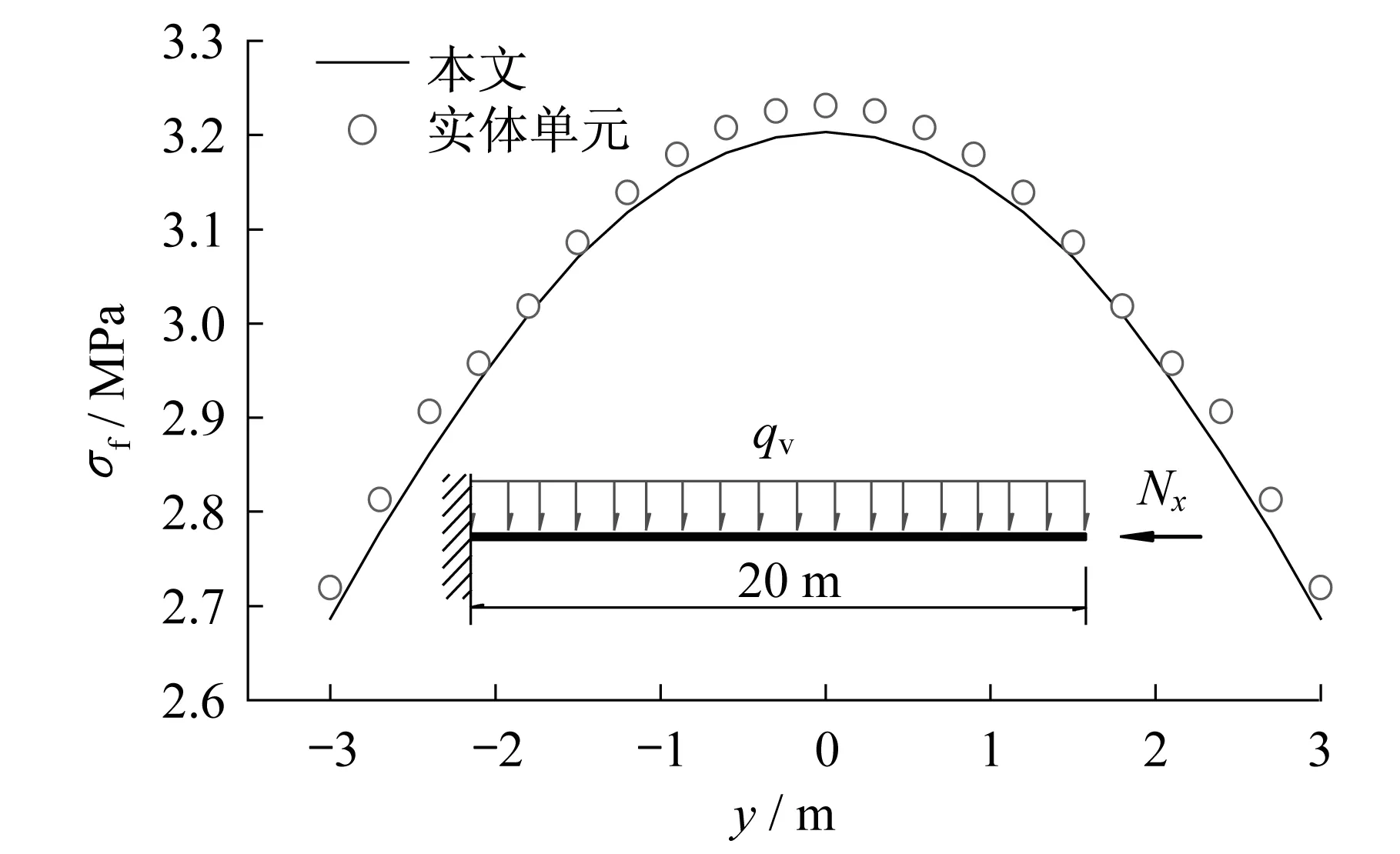
图11 悬臂梁跨中截面应力Fig.11 Stress on midspan section of cantilever girder
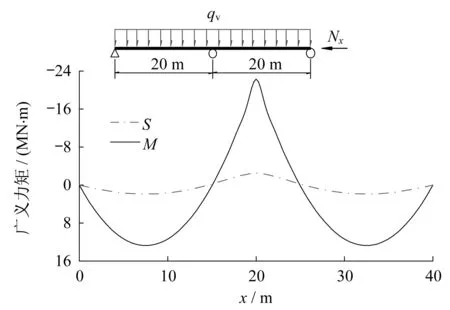
图12 连续梁的广义力矩图Fig.12 Generalized moment of continuous girder
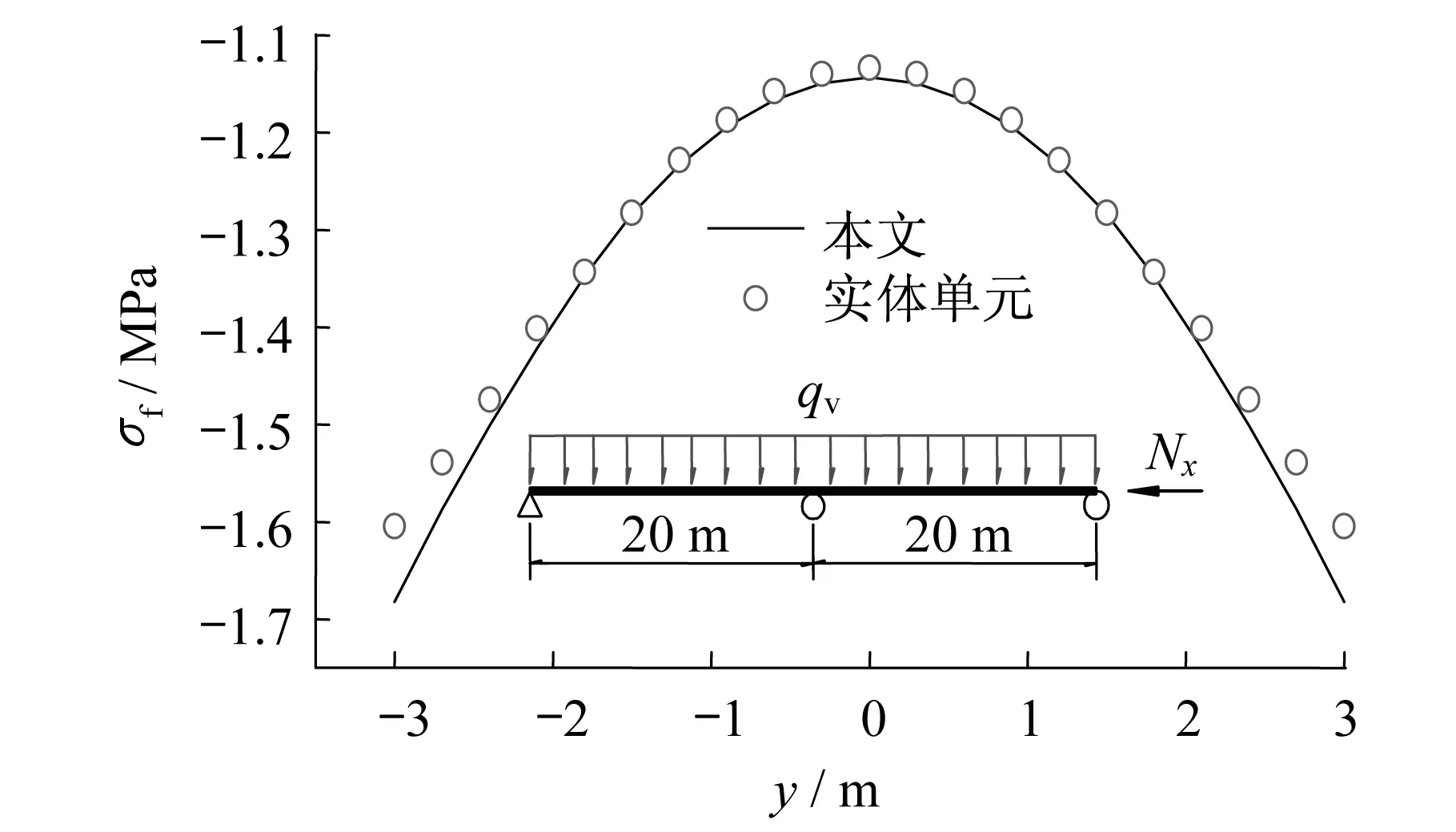
图13 连续梁跨中截面应力Fig.13 Stress on midspan section of continuous girder
5 结 论
本文通过引入轴向位移u(x),以合理描述压弯作用下截面的纵向位移状态,给出了轴向位移、竖向位移与剪力滞位移间相互耦合的微分关系,并利用解析解和边界条件建立了梁单元节点位移与节点力间的对应关系,从而导出了压弯作用下考虑剪力滞的Π形梁单元刚度矩阵。
通过对简支梁、悬臂梁和连续梁的位移与应力进行分析,本文方法能够较好地与实体单元分析结果相吻合,能够准确反映Π形梁的位移状态与受力状态,验证了本文方法的有效性和可靠性,并得出以下结论。
(1) 在压弯作用下,由于剪力滞的影响梁单元的轴向位移沿梁长不再按照直线变化,而随受力状态和边界条件的不同而改变。
(2) 连续梁中间支座处,轴向位移出现跳跃现象,跳跃方向沿轴力反向;
(3) Π形梁的剪力滞矩S和弯矩M具有相似的分布规律,但剪力滞矩S的绝对值远小于弯矩M的绝对值,轴向压力对广义力矩的影响可以忽略。
