基于Sym小波与BP神经网络的装配柱钢筋套筒灌浆连接缺陷检测方法

韩 笑 唐和生 周德源

(同济大学结构防灾减灾工程系,上海 200092)

0 引 言

随着近年来建筑工业化的大力推行,装配式建筑越来越多地出现在了我们的生活当中。装配式建筑具有施工速度快、环境污染小、节约人力等优点,具有显著的发展潜力。装配式结构与现浇结构的主要区别在于节点的连接性能,若能保证节点良好的连接性能,装配式结构完全可以代替现浇结构。有研究表明装配整体式管框架结构的地震损伤程度与普通框架结构相比,并没有明显的差别,但装配整体式框架结构的节点仍是其抗震中的薄弱环节[1]。装配式框架结构广泛用于商办项目,多数的装配式柱采用灌浆套筒与节点连接,其钢筋连接性能与结构的承载能力与抗震耗能能力密切相关。故有必要研究一种无损检测方法,以评估装配柱钢筋的连接性能。

结构构件的损伤会引起结构动力响应的变化,近年来,小波分析和BP神经网络成为了损伤检测的两大强有力的工具。小波分析具有低熵性、多分辨率、去相关性、选基灵活性;BP神经网络具有较强的容错性、冗余性以及自我更新能力,且理论上可以映射任何非线性关系。本文结合两种方法,对装配柱灌浆套筒连接的损伤识别方法进行探究。

1 装配式柱的数值模拟

1.1 计算模型

本文采用通用有限元软件ABAQUS建立数值模型,模型的尺寸与构造参考相关规范[2-3]。装配柱采用400 mm×400 mm矩形截面,柱高3 m,套筒连接长度为220 mm,轴压比取0.5。混凝土标号为C40,纵筋及箍筋均采用HRB400级钢筋。在激振方向上采用对称配筋,两端各配422,在非受力方向两侧各配腰筋220,箍筋选用8@100。在柱高中点处布置激振点,距柱底1/4高度处布置4个测点。具体尺寸配筋、纵向钢筋编号以及测点布置位置如图1所示。

在ABAQUS软件建模中,装配柱两端固接,钢材的密度取7 800 kg/m3,弹性模量取2.1×1011N/m2,泊松比取0.3;混凝土密度取2 500 kg/m3,弹性模量取3×1010N/m2,泊松比取0.2。混凝土采用三维实体缩减积分单元C3D8R,钢筋采用二节点直线桁架单元T3D2;刚性加载板与混凝土柱之间采用Tie约束;钢筋用Embedded方式植入混凝土中;模型采用振型模态法(取前50阶模态)计算冲击响应,采用模态阻尼,根据经验,前10阶模态阻尼取0.04,后40阶模态阻尼取0.05。模型的边界情况及网格划分如图2所示。

图1 装配柱截面详图(单位:mm)Fig.1 Detail of assembly column (Unit:mm)

图2 装配柱有限元模型Fig.2 Finite element model of assembly column

1.2 引入损伤

根据已有研究[4]可知,在装配工程中,套筒灌浆接头可能因气泡、堵塞、漏浆等造成各种灌浆缺陷,主要的套筒灌浆缺陷类型如表1所示。

可以看出,表中的缺陷类型对套筒连接性能的影响主要表现为削弱了钢筋与灌浆料的连接,将这些缺陷视为钢筋套筒连接段的弹性模量折减(当套筒与钢筋完全失去连接时,连接段弹性模量折减至0),将各编号钢筋连接长度范围内的弹性模量折减(由于套筒连接质量缺陷造成)作为数值模型中的损伤引入,按下式计算:

表1套筒灌浆缺陷类型

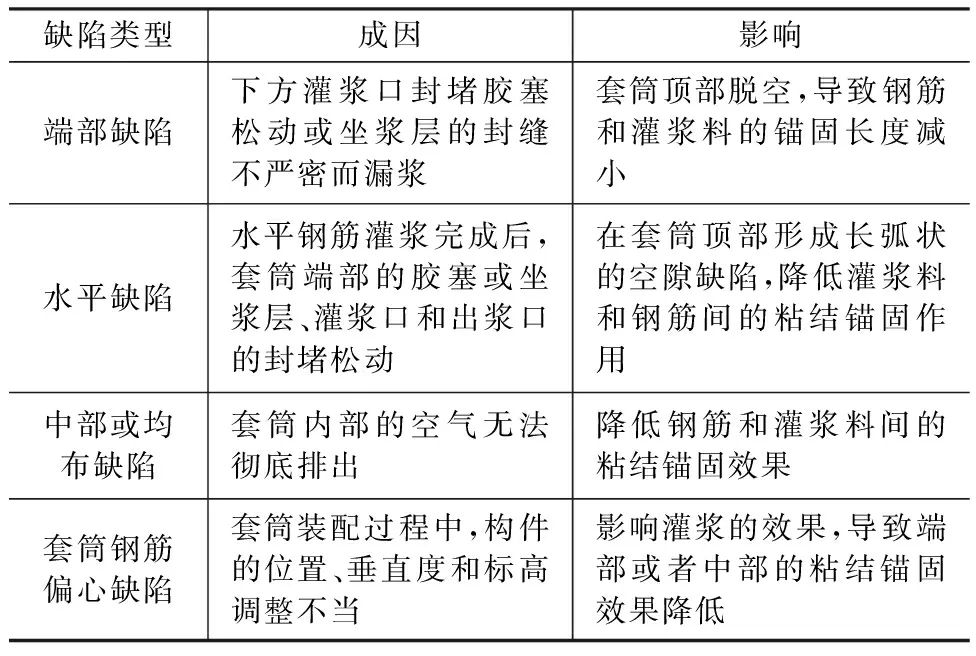
Table 1Type of sleeve grouting defect

(1)

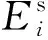
在后文中,以Di-di表示编号为i的钢筋损伤di,如D1-0.7表示编号为1的钢筋在连接段内弹性模量折减70%。

1.3 加载与数据采集

模拟检测时的锤击[5],在模型激振点处施加一个瞬态半波正弦冲击力:

(2)

式中:P(t)为作用在激振点的一个瞬态半波正弦冲击力;P0为冲击波的幅值,取10 kN;T取为装配柱的一阶自振周期,经有限元软件计算,约为6.5 ms。

在有限元模型中,每1 ms采集一次数据,总共采集时间为200 ms,以详细地记录模型的响应信息。

2 基于小波分解的能量特征值提取

2.1 小波变换

在计算机中,多采用二进制动态采样网格,每个节点对应的尺度为2i,平移为2ik。根据此得到离散化小波函数[6-7]:

(3)

式中,i,k∈Z,ψi,k(t)称为二进小波。

本文通过Matlab软件来实现小波变换。

2.2 Sym8小波基

小波变换的一个关键点在于小波基的选取,因Symlets系列小波是有限紧支撑正交小波,其时域和频域的局部化能力均较强,特别是在数字信号的处理中,可以提供有限长的更实际、更具体的数字滤波器[5],故本文采用Sym8小波作为小波变换的小波基。Sym8小波基的小波函数及尺度函数如图3所示。

图3 Sym8小波函数及尺度函数Fig.3 Sym8 wavelet function and scale function

2.3 能量特征值提取

将信号进行小波分解后,可以得到信号中若干频带成分的信息,当结构发生损伤时,因损伤对响应信号各频带成分的作用不同,可能抑制,也可能增强,从而导致各频带成分的相关参数重新分布[8],因此,带损伤的装配柱与未带损伤的装配柱相比,其响应信号中个频带所携带的能量占比也会发生改变,故提取能量占比变化显著的分解层次所对应的能量变化百分比作为结构的特征值。

利用小波分析,将各测点所得到的加速度响应一维原始信号进行分解层次为8层的小波分解,以P1测点为例,未损伤时的各成分如图4所示。图中,S表示原始信号,d1到d8分别表示由高到低的第1层到第8层高频分量,a8表示第8层低频分量。

图4 钢筋未损伤时的加速度响应小波分析Fig.4 Wavelet analysis of acceleration response with undamaged reinforcements

将8层高频分量与第8层低频分量做能量统计。经过j-1层小波分解(含j-1个高频分量,1个低频分量),原始信号S(t)可以写成[9]:

(4)

其中

(5)

(6)

信号S(t)的总能量为

(7)

由小波基的性质可得

(8)

(9)

各频带能量占比变化量为

(10)

以P1测点所采集信号的能量占比变化量为例,对比几种不同编号钢筋不同损伤程度的工况,以选出对损伤敏感的分解层次。对比情况如图5所示。

图5 各分解层次能量占比变化量Fig.5 Change in energy ratio of each decomposition level

可以看出,分解层次为高频成分d2,d3以及低频成分a8(在图5中分别对应1,2,9)的能量占比变化量对损伤最为敏感,对同一编号的钢筋,损伤程度越大,ΔP2越大,ΔP3,ΔP9越小。故将ΔP2,ΔP3,ΔP9作为能量特征值。

3 基于BP神经网络的缺陷识别

3.1 BP神经网络关键参数选取

BP神经网络具有强大的映射能力及自我更新特性[10],其基本原理是将误差从输出层向输入层传播,并沿途调整各层间的连接权值与阀值,使误差不断减小,直至达到合理的精度,以实现训练网络的目的。其误差目标函数为

(11)

每次训练所调整的第m-1层到第m层的权值增量Δw由下式计算:

(12)

式中,lr为学习速率,取0.01。

选择非线性激励函数tansig作为网络的激励函数,其表达式为

(13)

采用Levenberg-Marquardt(L-M)规则训练网络,可以很大程度减小网络训练时间[11];输出层以线性函数purelin作为神经元的激励函数,不仅减少平坦区现象,而且有利于消除非线性函数造成的畸变现象[12]。

神经网络的训练样本与网络拓扑之间并无确切的数量关系,常根据下式估计各参数值[13]:

(14)

式中:NP为训练样本数;h为隐含层节点数,本文采用54个样本用以训练网络,输入向量维数p为3,输出向量维数q为1,故取h为12。

3.2 确定输入与输出参数

如2.3中所述,选取第2层、3层高阶频带与第8层低阶频带的能量占比变化量,在数值模型中,布置了4个测点(P1,P2,P3,P4),每个测点获得的原始信号均能得到一组变化量,将四个测点的变化量取平均,作为神经网络的输入参数组{ΔP2,ΔP3,ΔP9}。

定义神经网络的输出参数分别为弹性损伤系数{ED}与塑性损伤系数{PD},两者对应的神经网络分别为Enet与Pnet。

当连接段钢筋受到损伤时,连接段截面的刚度损失δEI为

(15)

则定义弹性损伤系数ED为

(16)

式中:δEi为第i根钢筋的等效损伤弹性模量折减量;Ai为第i根钢筋的面积;li为第i根钢筋到弹性中和轴的距离。

对于塑性损伤系数,其与截面进入完全塑性状态时中和轴的位置相关,本文中取装配柱的轴压比为0.5,其塑性损伤时的中和轴近似认为在截面高度中间(即在完全塑性阶段往复荷载作用下,中和轴的位置不变),当连接段钢筋受到损伤时,截面进入全塑性状态时,连接段截面的抵抗矩损失δM为

(17)

则定义塑性损伤系数PD为

(18)

式中,ri为第i根钢筋到塑性中和轴的距离。

3.3 网络训练生成

采用数值模拟得到的输入输出参数来训练神经网络,可以获得大量的数量样本,相较于实际模型而言,可以有极大地降低成本,并且可以覆盖较大范围的损伤情况与损伤程度[14]。用于训练网络的损伤工况如表2所示。

表2训练样本损伤引入情况

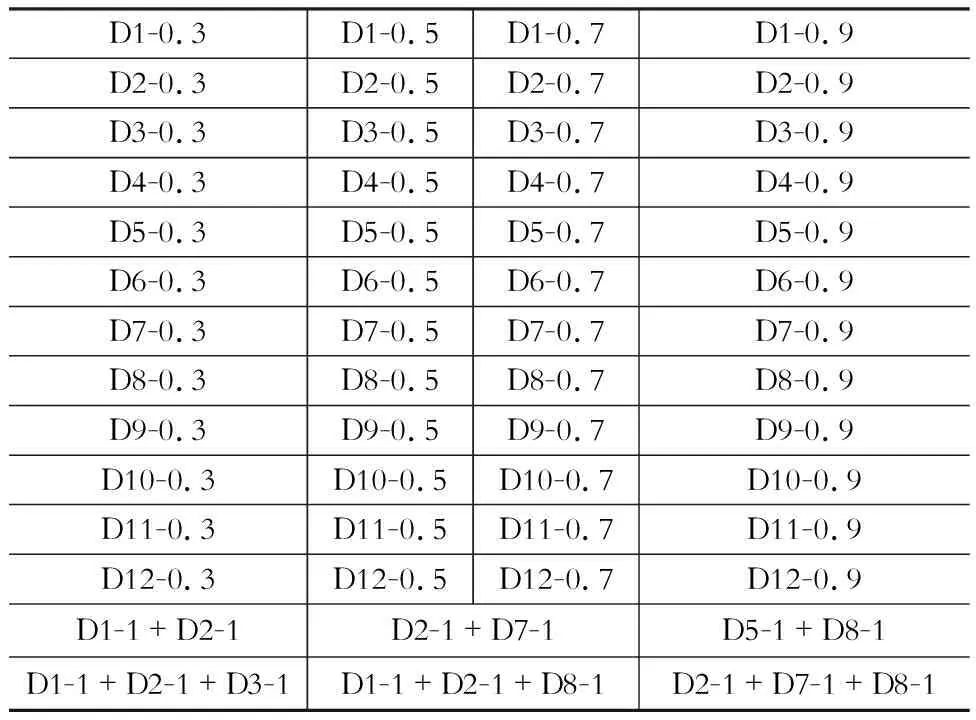
Table 2Damage introduction of training samples

对于识别弹性损伤的神经网络Enet,选取隐层层数为1,其余参数如3.1中所述,训练结果如图6所示。

图6 Enet训练结果Fig.6 Enet training results

网络训练完成后,迭代总次数为69次,最终的均方差为0.000 293,最小梯度为0.005 27。Training (训练)、Validation (验证)、Test (测试)、All (总体)的相关系数R均十分接近1,说明训练得到识别弹性损伤的神经网络是满足要求的。

对于识别塑性损伤的神经网络Pnet,选取隐层层数为3,其余参数如3.1中所述,训练结果如图7所示。

网络训练完成后,迭代总次数为91次,最终的均方差为7.27×10-5,最小梯度为0.001 63。Training (训练)、Validation (验证)、Test (测试)、All (总体)的相关系数R也都十分接近与1,说明训练得到的识别塑性损伤的神经网络同样是满足要求的。

3.4 网络识别能力测试

为了检验训练得到的Enet与Pnet对弹性损伤与塑性损伤的识别效果,利用有限元软件模拟多种损伤工况,用以检验网络。损伤工况及检验结果如表3、表4所示。

图7 Pnet训练结果Fig.7 Pnet training results

表3弹性损伤测试结果

Table 3Results of elastic damage test

由两表可以看出,对于弹性损伤,Enet的识别准确度较高,除工况D3-1+D5-1+D12-1外,其余工况的识别相对误差均在5%以下,说明对于套筒连接的等效弹性损伤,BP神经网络的识别是准确的;对于塑性损伤,Pnet的识别准确度不理想,一个重要的原因是训练的输入参数是由弹性响应得来的,弹性损伤系数ED直接和弹性响应相关,而塑性损伤系数PD与弹性响应不直接相关,导致其识别精度不如ED。

表4塑性损伤测试结果

Table 4Results of plastic damage test

大多数情况下,ED值大于PD值,故若ED值小于塑性损伤的最大允许值,那么实际的PD值也是满足要求的。

4 结 论

本文通过通用有限元软件ABAQUS建模,模拟实际检测中的瞬态冲击,提取结构响应数据,利用Sym8小波分析提取装配柱的弹性响应曲线的各个频带成分的能量占比,并选取能量占比变化量最大的三个频带的能量占比变化值构成能量特征值。将四个测点的能量特征值取平均,构造维数为3的特征向量作为BP神经网络的输入向量,定义了弹性损伤系数与塑性损伤系数,用以分别作为神经网络的输出值。通过数值模拟的方法获得多种损伤工况下的训练样本用以训练网络,并获得一系列测试样本用以检测网络的识别能力。结果表明,训练得到的神经网络可以进行装配柱套筒连接缺陷程度的识别,为实际工程中的检测给出了参考。