一种新的考虑接触角的弓网接触模型

周 宁，蔚 超，邹 欢，邹 栋，张卫华，赵 晨

(1. 西南交通大学 牵引动力国家重点实验室，成都 610031;2. 广州铁路(集团)公司，广州 510000)

随着高速电气化铁路的快速发展，弓网系统动力学研究作为车辆大系统动力学研究的主要分支之一，对高速列车稳定受流起着至关重要的作用。由于接触网系统距离长、跨数多，导致试验平台搭建困难，除少数单位拥有受电弓—接触网地面模拟试验台外[1-2]，研究人员主要通过仿真计算进行弓网系统动力学研究[3-6]。作为弓网耦合系统仿真计算的关键技术，弓网接触模型对动力学响应有着重要影响。传统接触模型通过罚函数法模拟弓网接触，通过调整罚刚度因子以真实反映弓网之间的接触行为[7]。在罚函数法的基础上，Collina等[8]在接触模型中加入了线性阻尼项，分析弓网接触中速度项的作用，以考虑弓网接触过程中的能量损失。Lankarani等[9]基于赫兹接触理论，提出了一种连续接触力模型以模拟多体系统碰撞过程中的相互作用，并推导了相关公式，此后诸多学者采用此接触模型进行弓网动力学方面的研究[10-11]。

无论是传统接触模型或赫兹接触模型，都仅考虑了受电弓与接触网之间在垂直方向上的接触行为。然而在列车实际运行过程中，受接触网波动以及接触线不平顺等因素的影响，受电弓与接触网的接触将偏离垂直方向[12]，由此也造成接触线在弓网接触点位置的切向与水平方向存在一定的夹角，这里将该夹角称之为弓网接触角。由此，本文通过考虑弓网滑动接触过程中实际存在的接触角的影响，对Lankarani等提出的赫兹接触模型进行修正，提出一种新的考虑接触角的弓网接触模型，然后与传统接触模型和赫兹接触模型进行对比，研究不同接触模型对弓网系统动力学性能的影响，对不同接触模型的合理性和适用范围进行分析。

1 受电弓—接触网模型

1.1 接触网模型

将接触线、承力索和弹性吊索等效为欧拉梁结构，吊弦简化为两端具有集中质量的弹簧结构，同时将定位器及支撑杆简化为质量-弹簧系统，选用质量单元和弹簧单元模拟简化系统。通过有限单元法提取接触网模态信息，进而采用模态叠加法建立总共包含十跨的接触网模型，单跨接触网模型结构及参数如图1所示。

图1 接触网单跨模型Fig.1 Single span model of catenary

接触网运动微分方程可表示为

(1)

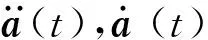
(2)

求解模态空间下广义坐标u(t)后，通过坐标反变换即可得到系统响应a(t)。

1.2 受电弓模型

诸多学者对受电弓建模方法已进行了大量研究，形成了比较完备的受电弓模型库[13]，如多刚体模型，归算质量模型以及刚柔混合模型等，其中以归算质量模型的应用最为广泛，图2和表1分别给出了这里采用的归算质量模型以及参数，其运动微分方程为

(3)

式中：Mp，Cp，Kp分别为受电弓质量归算模型的质量、阻尼及刚度矩阵;up为垂向位移，Fp为载荷向量。

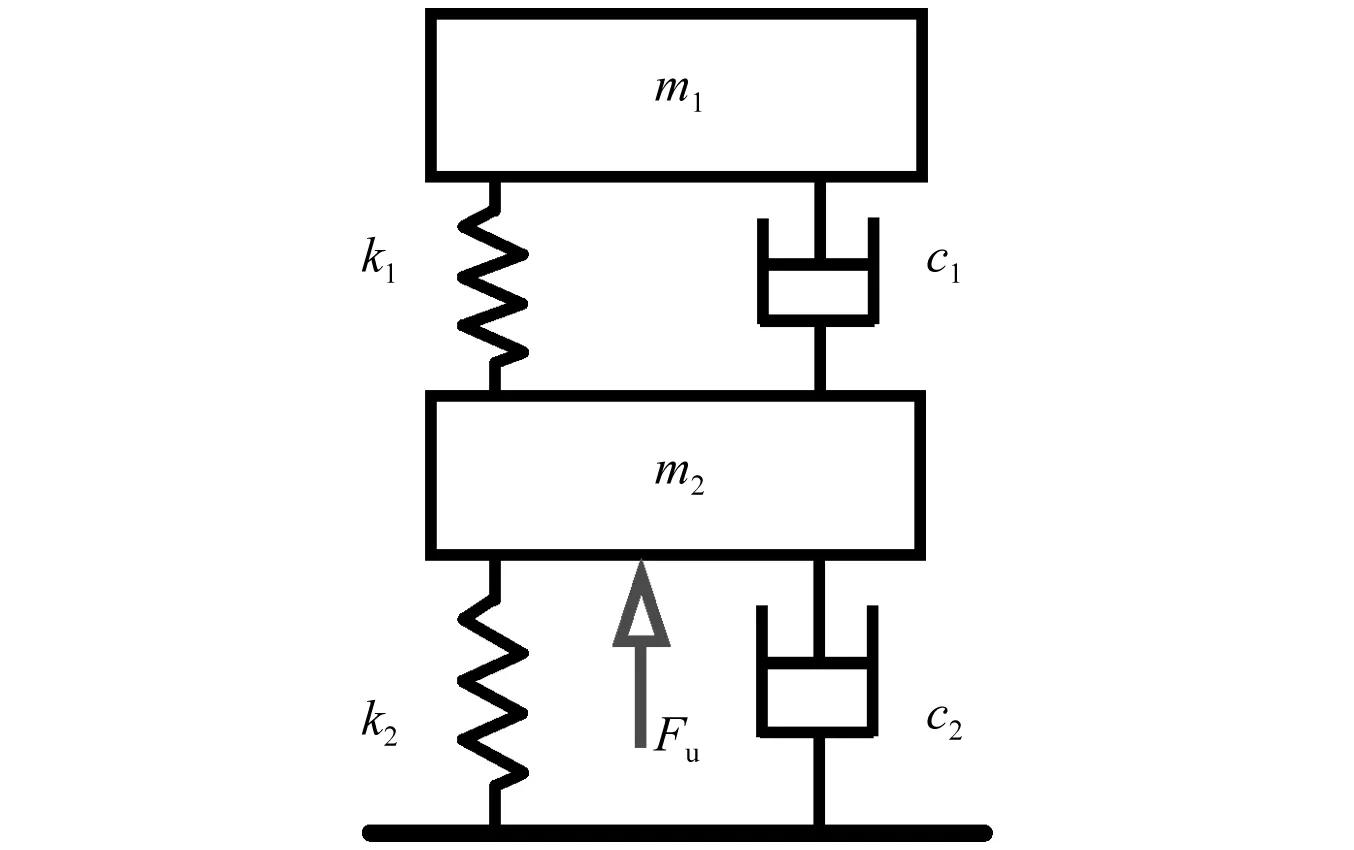
图2 受电弓归算质量模型Fig.2 Lumped mass model of pantograph表1 受电弓等效参数Tab.1 Pantograph equivalent parameters

参数数值弓头质量m1/kg7.2框架质量m2/kg15弓头刚度k1/(N·m-1)4 200框架刚度k2/(N·m-1)50弓头阻尼c1/(N·s·m-1)10框架阻尼c2/(N·s·m-1)90静态抬升力Fu/N120

1.3 弓网耦合模型

组合受电弓与接触网模型可得弓网耦合动力学模型，其运动微分方程为

(4)

其中，式(4)等号右端为受电弓—接触网系统的载荷向量，该向量是与弓网间接触力Fc相关的向量。对于弓网间接触力，采取如下三种方式进行描述。

1.3.1 经典接触模型

传统经典接触模型计算简单，效率较高，在弓网动力学仿真分析中应用也较为广泛。该模型是基于罚函数法引入接触刚度来模拟弓网间接触力，接触力表达式为

(5)

式中:Fc为接触力;Kc为接触刚度;up和uc分别为受电弓和接触线垂向位移。

1.3.2 赫兹接触模型

受电弓沿接触线滑动接触过程中，时常伴有冲击、碰撞过程的发生。从碰撞的角度分析，接触力不仅与受电弓和接触网的相对位移有关，也与其速度项相关。Lankarani等基于赫兹接触理论，通过考虑迟滞阻尼效应，提出了一种连续接触力模型，并推导了相关公式，用于描述多体系统碰撞过程中的接触力。葡萄牙学者Rauter首先将该接触模型引入弓网仿真分析中，其接触力表达式如式(6)所示

(6)

1.3.3 新接触模型

对于上述经典接触模型和赫兹接触模型，主要考察受电弓与接触网在垂直方向的接触行为。然而在列车实际运行过程中，受接触网波动以及接触线不平顺等因素的影响，受电弓与接触线的接触法向将偏离垂直方向，由此也造成弓网间接触角θc的存在，图3描述了实际的弓网接触关系。

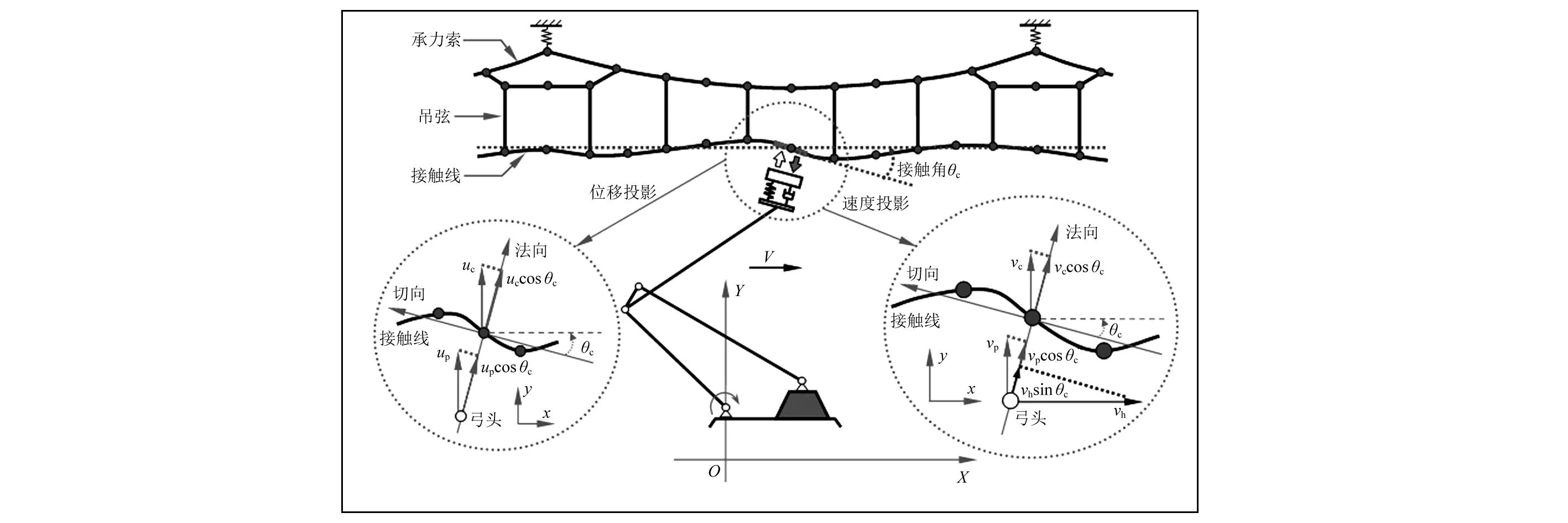
图3 弓网实际接触关系图Fig.3 Contact relationship between pantograph and catenary

当考虑弓网间接触角时，弓网间相对位移应为垂向相对位移(up-uc)在接触法向上的投影，由此与相对位移相关的接触力部分为

FK=Kc(up-uc)n(cosθc)n

(7)

式中:up和uc分别为受电弓和接触网的垂向位移;θc为弓网间接触角，接触线切线与水平方向夹角以逆时针方向为正。

类似的，在计算弓网间相对运动速度时，也需将弓头和接触线的垂向速度以及列车速度沿接触法向进行投影，如图3所示，由此弓网沿接触法向相对速度为

(8)

式中:vp和vc分别为受电弓和接触网的垂向速度;vh为列车速度。

进而，与相对速度相关的接触力部分可写为

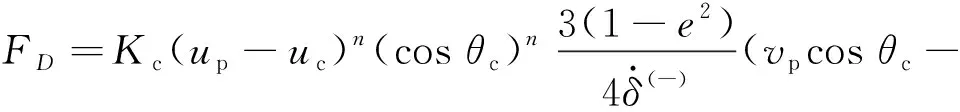
(9)

由此，对于考虑接触角时的新接触模型，接触力表达式为

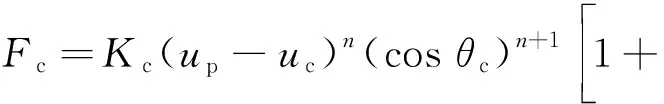
(10)

2 计算结果及分析

2.1 三种接触模型计算结果对比

针对上述弓网系统，通过自编程序，分别采用经典接触模型，Lankarani赫兹接触模型以及所提出的新接触模型进行弓网系统动力学仿真，计算速度等级包括100 km/h,200 km/h,300 km/h和400 km/h四个工况，图4和图5分别为提取的3～7跨内弓网接触力统计值和接触力变化曲线。

(a) (b)图4 三种接触模型接触力统计值对比Fig.4 The comparison of contact force statistics between three contact models

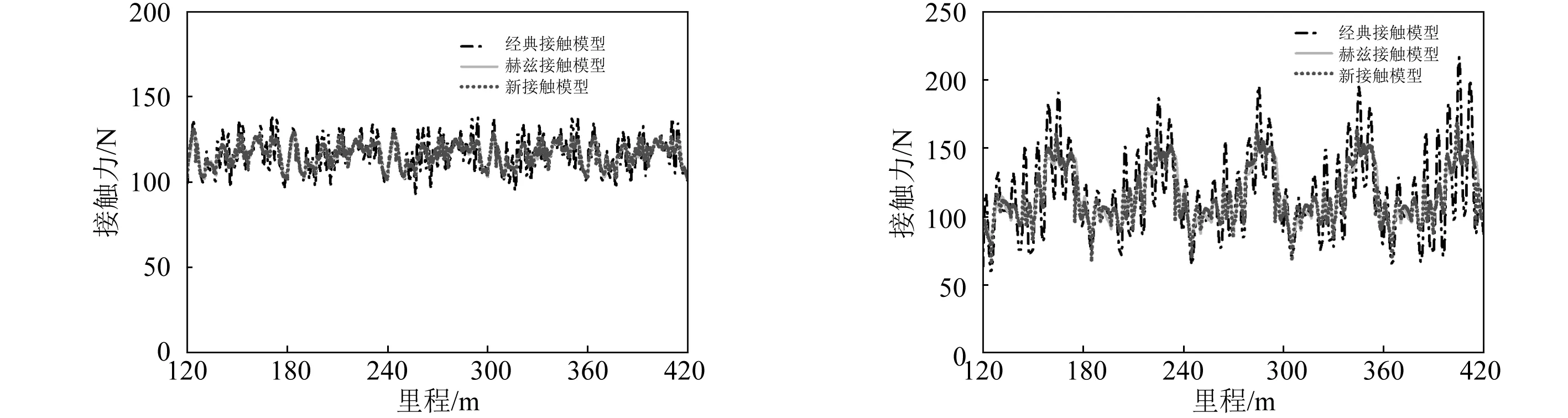
(a)v=100 km/h (b)v=200 km/h

(c)v=300 km/h (d)v=400 km/h图5 三种接触模型接触力随里程变化图Fig.5 The contact force variation with distance of three contact models

由图4可见，随着列车运行速度的提升，三种模型接触力均值变化较小，均在116 N附近。接触力标准差变化较大，其中经典接触模型和新赫兹接触模型接触力标准差随速度提升变化较大，而Lankarani赫兹接触模型变化相对较小。结合图5中的接触力随里程变化结果同时可见，当列车速度为100 km/h时，三种接触模型接触力曲线差异较小。随着速度等级的提升，相较于Lankaraini赫兹接触模型，基于经典接触模型和新接触模型得到的接触力表现出更大的振荡。但经典接触模型接触力的振荡在接触网各个位置均有体现，而新赫兹接触模型的振荡主要表现在定位点附近。

2.2 结果分析

与经典接触模型相比，Lankarani赫兹接触模型随速度等级的提升接触力标准差变化较小，在接触力里程图中接触力变化更为平缓，主要是由于Lankarani赫兹接触模型中引入了阻尼项，减缓了弓与网之间的冲击，从而使得接触力变化相对较小。

通过对比Lankarani赫兹接触模型以及新的接触模型表达式，可以看到两种模型的差异主要在于弓网间接触角θc的考虑。为考察弓网间接触角对接触力的影响，提取弓网间接触角随列车运行里程的变化关系，如图6所示。

(a)v=100 km/h (b)v=200 km/h

(c)v=300 km/h (d)v=400 km/h图6 弓网接触角随里程变化图Fig.6 Pantograph/catenary contact angle variation with distance

由图6可见，随着列车速度等级的提升，弓网接触角的变化幅度逐步增大，从一开始的0.2°提升到0.5°左右。同时可见，在定位点附近接触角的大小及其变化幅度较大，这与采用新接触模型计算的接触力在定位点附近的变化规律相符，而越靠近跨中接触角及其变化幅度越小。另一方面，通过计算发现cosθc=0.999 9≈1，sinθc=0.007≈0，接触角的影响理应较小，但考虑到列车运行速度要远大于弓网振动速度，因此不能单独以接触角的影响进行评判。为进一步对上述现象做出解释，以下对新接触模型中关键项vpcosθc,vccosθc和vhsinθc进行对比分析，如图7所示。

(a)v=100 km/h (b)v=200 km/h

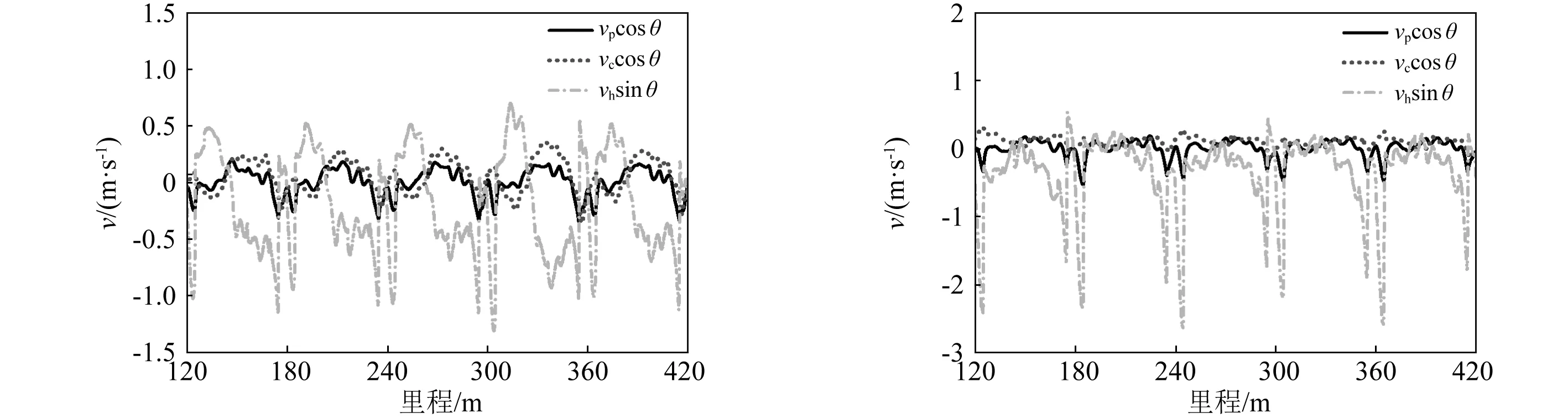
(c)v=300 km/h (d)v=400 km/h图7 接触力关键项vpcos θc,vccos θc和vhsin θc随里程变化图Fig.7 The contact force critical items vpcos θc, vccos θc and vhsin θc variation with distance

由图7可见，当列车速度较低时，接触模型关键项vpcosθc,vccosθc和vhsinθc基本处于同一量级水平；而随着速度提升，vhsinθc相较于vpcosθc和vccosθc逐步占据主导作用，而且随车速的增大越来越明显，特别是在定位点附近这种主导作用越强，越靠近跨中作用越弱。由此说明，在低速情况下，即vh较小时，vhsinθc与vpcosθc和vccosθc相当，因此低速情况下两种接触模型计算的接触力结果相差不大；但随着列车速度vh的提升，接触角θc迅速增大，尤其是在定位点附近，vh与θc共同作用使得vhsinθc远大于vpcosθc和vccosθc，因此在高速情况下新接触模型与Lankarani赫兹接触模型相比，计算的接触力会表现出更大的振荡，且这种振荡主要表现在定位点附近。

3 结 论

通过考虑弓网滑动接触过程中实际存在的接触角的影响，对Lankarani提出的赫兹接触模型进行修正，提出了一种新的弓网接触模型，并与传统接触模型和Lankarani赫兹接触模型进行对比，辨识了不同接触模型对弓网系统动力学性能的影响，通过分析得知：

(1)与弓网经典接触模型相比，Lankarani赫兹接触模型考虑了弓网接触中阻尼的影响，减缓了弓与网的冲击，使得接触力的变化更为平缓。

(2)与Lankarani赫兹接触模型相比，新接触模型考虑了列车速度和弓网间接触角对接触力的影响。当列车低速运行时这种影响较小，而高速运行时对接触力的影响较为明显，尤其在定位点附近影响较大，甚至会引发离线，而越靠近跨中影响越小。

(3)在低速运行时，弓网间阻尼以及接触角的影响较小，采用经典接触模型或Lankarani赫兹接触模型进行弓网动力学仿真即可满足要求。在高速运行条件下，阻尼以及接触角的影响不可忽略，采用新提出的接触模型进行弓网动力学仿真更为合理。