基于多层次修正的纤维增强复合薄壳动刚度预测

2019-01-23周正学薛鹏程韩清凯

振动与冲击 2019年2期

李晖，周正学，薛鹏程，韩清凯

(1.东北大学机械工程与自动化学院，沈阳 110819；2.东北大学航空动力装备振动及控制教育部重点实验室，沈阳 110819)

纤维增强复合薄壳(Fiber-Reinforced Composite thin Shell, FRCS)相对于金属薄壳，具有质量轻、承载压力大、抗冲击性能好、抗疲劳性能突出、绝缘性好等多种特点，目前正在被越来越多地应用于航空航天、船舶、海洋工程、石油化工、兵器制造以及核工业等重要领域[1]。工程实际中存在大量通过该类型材料制成的薄壳结构件，如航空发动机的复合材料机匣、海底深潜器用的复合材料耐压圆柱壳、液体火箭发动机燃烧室采用的耐高温复合材料壳体等，他们通常受到脉冲激励载荷的作用[2]。且随着它们的结构越来越复杂、工作环境越来越苛刻，其振动问题也越来越突出[3-6]。因此，研究脉冲激励下复合薄壳的动态特性具有重要的工程及学术意义[7-8]。

动刚度表征了结构系统抵抗动态载荷下的变形能力，由于该参数与外界激励频率密切相关，因而可以更加科学、客观地反应结构的动态性能[9]。目前，人们已经对常规金属、橡胶材料构成的各种宏观结构件的动刚度进行了研究，并取得了阶段性的研究成果。例如，Kaynia等[10]采用理论建模与试验相结合的方法，对支撑桩组的动刚度进行了分析。Marsh等[11]对精密轴承的动刚度进行了测试，以此来表征精密轴承的动态性能。Nakamura等[12]建立了土壤的有限元模型并通过对土壤动刚度的研究，提出了建筑物抗震的几种改进方法。Tileylioglu等[13]考虑动刚度的影响，并研究了大型地基测试结构在受到低频激励时的振动特性问题。Frangoudis等[14]对数控铣床夹具的动刚度进行了试验测试，并分析了不同切削速度对夹具动刚度的影响。石清鑫等[15]采用三维有限元法建立了高速动平衡机摆架的数学模型，并对其动刚度进行了计算分析，且与试验值进行了比较。袁占航[16]根据弹簧的滞回曲线，通过谐响应法计算了金属橡胶复合板弹簧结构的动刚度，并根据动刚度性能对结构进行了优化设计。李宇菲[17]对纤维增强复合材料板簧的动态特性进行了有限元分析，研究了端部受到正弦力作用下复合板簧的动刚度问题，并在此基础上进行了疲劳分析。欧鸣雄等[18]建立了立式循环转子部件支撑结构的有限元模型，并对支撑结构的动刚度进行了分析。邓四二等[19]在双列角接触球轴承动力学分析基础上，建立了双列角接触球轴承动刚度方阵分析模型，并研究了轴承结构参数和工况参数的变化对轴承动刚度的影响。

虽然人们已经对常规金属、橡胶材料构成的各种宏观结构件的动刚度进行了大量研究，但并未关注脉冲载荷作用下纤维增强复合薄壳的动刚度性能，也并未通过理论结合试验的方法，对其动刚度问题进行深入研究。为此，本文运用板壳振动理论、能量法、Simpson积分等方法、结合多层次修正技术对该类型复合薄壳的动刚度进行分析与预测，还总结概况出一套科学的预测方法和流程。最后，以T300碳纤维/树脂基复合薄壳为例，搭建了振动测试系统，并通过实际测试，验证了上述预测方法的正确性。

1 纤维增强复合薄壳动刚度求解

本文所研究的纤维增强复合薄壳是由N层具有正交各向异性特点的纤维和基体材料组合而成的，如图1所示。首先，圆柱壳中面作为参考平面，建立xθz坐标系。纤维方向与整体坐标系x轴方向的夹角为β，壳体长、厚度、中面半径分别为L，h和R，每一层位于z坐标轴较低表面hk-1和较高表面hk之间，每层的厚度均相同。图中的1代表纤维纵向，2代表纤维横向。假设纤维增强复合薄壳平行纤维方向的弹性模量为E1，垂直纤维方向的弹性模量为E2，1-2平面内的剪切弹性模量为G12，任意一激励点为Pa，任意一响应点为Pb，相对于1方向作用应力引起1方向、2方向应变的泊松比为μ1，2方向作用应力引起1方向、2方向应变的泊松比为μ2。

图1 纤维增强复合薄壳理论模型Fig.1 The theoretical model of FRCS

根据板壳振动理论，将复合薄壳任意一点的位移表达成如下形式[20]

(1)

式中：u，v，w为壳内任意一点的位移；A，B，C为振型幅值系数；n为复合薄壳的周向波数；ω为圆频率；φ(x)为不同边界条件下的函数。

对于正交各向异性材料，其平面应力状态主方向对应的应力-应变关系为

(2)

其中，

当材料主轴方向与整体坐标系之间有一定夹角β时，用应力-应变转轴公式计算得到第k层壳体在整体坐标系下的应力-应变关系为

(3)

其中，

式中:k为复合薄壳的第k层；βk为第k层薄壳的纤维方向与整体坐标系x轴的夹角。

薄壳的动能可用式(4)表示

(4)

式中：ρ为纤维增强复合薄壳的密度。

根据经典的板壳振动理论，薄壁圆柱壳的应变能U可表示为

(5)

式中：εT为应变向量，其表达式为

εT={εx,εθ,γxθ,kx,kθ,χxθ}

(6)

式中：各个向量元素具体表达式详见文献[21]。

对于纤维增强复合薄壳结构，其薄膜刚度矩阵S定义如下

(7)

其中，

式中：Aij,Bij和Dij分别为拉伸、耦合与弯曲矩阵。第k层的上表面与下表面到参考平面的距离分别为hk与hk+1。

将位移式(1)和应力式(2)代入式(4)和式(5)中，可以得到复合薄壳的最大动能和最大应变能分别为Tmax和Umax。

定义拉格朗日能量函数L的表达式为

L=Tmax-Umax

(8)

求解纤维增强复合薄壳的固有频率问题，即是求解使L有最小值的所有待定参数，即有

(9)

为了求解方便，将式(9)写为矩阵形式为

(K-ω2M)a=0

(10)

式中：K,M分别为结构刚度矩阵和结构质量矩阵，广义位移向量a=(A,B,C)T。

令式(10)的行列式为0，即可求得复合薄壳的固有频率，设求得的圆频率值为ωmn，将求得的圆频率值ωmn回代到式(10)中可得到各个阶次的模态振型A，B和C。

在求解获得复合薄壳固有频率和模态振型的基础上，采用振型叠加法求解复合薄壳在脉冲激励下的时域振动响应。假设脉冲激励载荷F(x,θ,t)作用于壳体的任一点Pa位置，如图1所示，其表达式为

F(x,θ,t)=f(t)δ(x-x1)δ(θ-θ1)

(11)

(12)

式中：x1和θ1为激励点Pa的坐标值;f0为激励幅值;t1为激励作用的时间;Ta为激励信号的周期，当其取值较小，且取t1为周期时间的二分之一长度时，可以用正弦半波信号来近似模拟脉冲激励信号，此时复合薄壳沿w方向的振动响应可表示为

X(t)=w(x1,θ1,t)Tmn(t)

(13)

式中：w(x1,θ1,t)为模态振型;Tmn(t)为各阶振型分量。

根据圆柱壳振动微分方程，在考虑等效黏性阻尼系数的情况下，通过化简，可以得到关于Tmn(t)的二阶常微分方程为

(14)

式中:ζ为模态阻尼比，其值通过试验测得；Gmn(t)为广义力，其表达式为

(15)

式中：Mmn为广义质量，其表达是为

(16)

将式(15)和式(16)代入式(14)中，并用杜哈梅积分可在零初始条件下，获得复合薄壳的强迫振动响应为

(17)

最后利用Simpson积分法对式(17)进行求解，并将其代回至式(13)，即可采用振型叠加法求得脉冲激励F(x,θ,t)作用下复合薄壳的任意一点的振动响应。

由式(13)可知，在激励点Pa处施加F(x,θ,t)的脉冲激励，可计算获得复合薄壳的任一响应点Pb的振动响应w(x,θ,t)。根据频响函数的定义，对于线性结构系统，可以将任一响应点Pb相对于激励点Pa的频响函数Xba(ωmn)表示为

(18)

式中：ωmn为激励频率，而w(ωmn)和F(ωmn)则分别为时域信号w(x,θ,t)和F(x,θ,t)经过傅里叶变换后获得的频域信号。

由于振动响应w(x,θ,t)已经被表示成位移形式，根据动刚度与频响函数的关系，可将复合薄壳任一响应点Pb相对于激励点Pa的动刚度表示为

(19)

2 基于多层次修正的复合薄壳动刚度的预测原理

模型修正技术中应用最为广泛的方法为灵敏度方法，但该方法的精度和收敛性容易受到设定的初始值和迭代过程中变量大小范围的影响，而多层次修正技术则可以通过选择较大的步长，使得初始状态的数值最大可能性的逼近理论值，来避免这一缺点。该修正技术主要源于多层次建模思想，于2004年被文献[22]首次提及，本文将其应用于复合薄壳动刚度的预测研究中，在层层修正的过程中通过反复迭代计算，来逐步提高动刚度预测的精度。

由于复合薄壳在制备过程中，其结构尺寸参数存在不均匀性问题，特别是其厚度容易产生较大偏差，而且即使同一批次生产的复合薄壳，其材料参数也存在一定的分散性。不仅如此，复合薄壳的模态阻尼比与动刚度预测密切相关，因此，准确确定模态阻尼比的取值是能否准确预测动刚度的关键。

首先，建立复合薄壳的理论模型，计算获得复合薄壳的固有频率和模态振型，并通过试验模态测试获取复合薄壳各阶固有频率和模态振型。然后，在第一层次修正环节，对理论模型中复合薄壳的长度、半径和厚度等参数进行修正，通过反复迭代方法，使理论计算与测试获得的固有频率误差efreq处于允许范围内(例如10%～15%)，即可完成第一层次的修正；在第二层次修正环节，则对复合薄壳纤维纵向、横向弹性模量、剪切模量、泊松比等参数进行修正，当计算获得的固有频率与测试获得的误差efreq处于更小范围内(例如5%～10%)，即视为完成第二层次修正；进一步，在第三层次修正环节，对复合材料各阶次模态阻尼比进行修正。通过试验获得各阶次模态阻尼比和脉冲激励下振动响应的频谱。然后，将测试获得响应频谱，与理论计算获得的响应频谱峰进行比较，直到响应频谱峰值的最大误差eres处于允许的范围内时(例如小于10%～15%)，即可认为完成第三层次修正。最后，根据频响函数的定义及其与动刚度的关系，则可较好地实现复合薄壳动刚度的预测，图2给出了基于多层次修正的复合薄壳动刚度预测的原理图。

图2 基于多层次修正的复合薄壳动刚度预测原理图Fig.2 Prediction principle diagram of dynamic stiffness of composite shell based on multilevel correction technique

3 纤维增强复合薄壳动刚度预测流程

本文在第一、二部分明确了基于多层次修正的复合薄壳振动响应的求解及预测原理。接下来，利用Matlab软件编写了相应的分析计算程序，并提出了纤维增强复合薄壳动刚度预测流程，可分为如下几个步骤：

步骤1 建立复合薄壳理论模型。

首先，需要给出纤维增强复合薄壳的长度、半径、厚度及每层纤维角度等几何参数。然后，输入纤维纵向和纤维横向的弹性模量、剪切模量、泊松比、模态阻尼比和密度等材料参数，建立复合薄壳几何模型。

步骤2 求解复合壳的动能和应变能最大值。

根据正交各向异性材料的特点，考虑纤维方向的影响，推导获得纤维增强复合薄壳的应力-应变关系式(3)，进而获得复合薄壳所受拉伸、耦合与弯曲矩阵表达式。随后将复合薄壳位移表达式(1)分别代入动能、应变能的表达式中，并略去谐波分量，即可得到复合薄壳的动能、应变能最大值的表达式Tmax和Umax。

步骤3 初步计算固有频率和振型。

将复合壳的动能、应变能和外激励做功最大值的表达式Tmax,Umax代入式(8)中，可以计算获得能量函数L的表达式。根据Ritz法，将能量函数L对所有待定参数求偏导，可以得到薄壳振动的特征方程表达式(10)，求解此特征值和特征向量问题即得到复合薄壳的某一阶固有频率以及对应的模态振型，重复以上步骤可依次获得各阶模态的固有频率值以及模态振型。

步骤4 基于第一层次修正复合薄壳的尺寸参数。

以实际测量所获得的复合薄壳尺寸参数为基准，考虑5%～10%的误差，选取合适的步长构造尺寸参数迭代向量L,R和h，接下来，对尺寸参数进行迭代，并以测试获得的复合薄壳固有频率和模态振型作为修正目标，当理论计算与测试获得的模态振型保持一致，且固有频率误差efreq处于允许范围内时(例如efreq≤10%～15%)，便可认为完成第一层次的修正。

步骤5 基于第二层次修正复合薄壳在纤维各个方向的弹性模量和泊松比。

步骤6 基于第三层次修正复合薄壳的模态阻尼比。

同样，选取合适的步长构造模态阻尼比迭代向量ζ1,ζ2, ,ζNT, 考虑10%～20%误差，其中NT为截取的阶次，通过对各阶次模态阻尼比进行不断迭代，并以锤击测试获得的复合薄壳某阶固有频率附近的振动响应作为修正目标，当理论计算获得的响应频谱峰值与测试获得的响应频谱峰的最大误差eres处于允许的范围内时(例如eres≤10%～15%)，即可认为完成第三层次修正，且认为此时各阶次模态阻尼比ζ1,ζ2, ，ζNT即为复合薄壳的各阶次对应的模态阻尼比。

步骤7 基于修正后的理论模型，准确预测复合薄壳任一响应点相对于激励点的动刚度。

由于振动响应w(x,θ,t)已经被表示成位移形式，根据动刚度与频响函数的关系，基于修正后的复合薄壳理论模型，并根据式(19)可求解获得复合薄壳上任一响应点相对于激励点的动刚度。

4 试验研究

本文以T300碳纤维/环氧树脂基复合薄壳为研究对象，对其固有特性进行了测试，其长度为150 mm，内半径为132.5 mm，厚度为3 mm，密度ρ=1 570 kg/m3，纤维纵向弹性模量E1=134 GPa，纤维横向弹性模量E2=8.5 GPa，剪切模量G12=3.36 GPa，泊松比v12=0.30。该类型复合薄壳为对称正交铺设，即[±45]12，共有24层，且每一铺层具有相同的厚度和纤维体积分数。

首先，搭建如图3所示的纤维增强复合薄壳振动测试系统，该系统有效利用了激光测振测试精度高、非接触测试的优点，通过自主设计开发的旋转扫描装置，来灵活、快速地获取复合薄壳任一测点振动响应。该旋转扫描装置可沿壳体中心线，实现360°的圆周扫描以及任意高度的调节，通过45°反光镜，可将Polytec PDV-100激光多普勒测振仪发出的竖直方向激光束转化到水平方向。接着，采用PCB-08C01力锤对该类型复合薄壳进行模态测试，其中，3个响应点1、点2以及点3坐标分别为(L,0,R)、(L/5,π,R)以及(L/2,π/3,R)，而锤击点4的坐标为(L/2,0,R)。同时，通过LMS 16通道数据采集分析仪和DELL移动工作站记录激励信号和响应信号并生成频响函数，进而辨识获得复合薄壳的各阶固有频率、振型和阻尼比。

图3 纤维增强复合薄壳振动测试现场图Fig.3 TheFigure of vibration testing system of FRCS

测试时设定的参数如下：①采样频率为6 400 Hz；②频率分辨率为0.067 Hz；③脉冲信号窗函数-力指数窗；④脉冲激励峰值为129.95 N；⑤响应信号窗函数-指数窗；⑥使Simpson积分处理操作来获得振动位移响应。图4(a)和图4(b)分别给出了锤击点4的脉冲激励时域信号和响应点1对应频域信号。

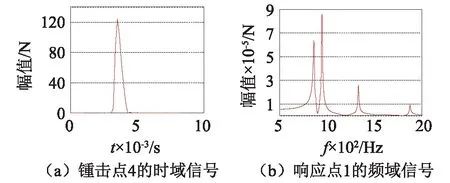
图4 脉冲激励时域信号和响应频域信号Fig.4 The impulse excitation signal and response signal in time domain and frequency domain

在测试获得固有频率和振型数据的基础上，按照第3部分提出的预测流程：一方面，计算获得复合薄壳的固有频率和振型；另一方面，在相同的测点位置和脉冲激励幅度下，计算获得多个测点的振动响应。然后，基于多层次修正技术对理论模型中的厚度、长度、半径、弹性模量、泊松比以及各阶次模态阻尼比进行修正，直到固有频率误差efreq<5%～10%，且响应频谱峰的最大误差eres<10%～15%。为了方便比较，将采用多层次修正技术后计算获得固有频率和振型结果一并列入表1中。

表1 采用多层次修正技术后计算和测试获得的纤维增强复合薄壳前6阶固有频率和模态振型Tab.1 The first 6 natural frequencies and modal shapes of FRCS obtained by experiment and calculation after using multilevel iterative correction technique

另外，为了说明多层次修正技术的优势，以响应点1为例，表2分别给出了测试、修正前和修正后获得的前3阶固有频率和振动响应。对表1和表2的结果分析可知，采用多层次修正技术后，计算获得的复合薄壳的固有频率和振动响应都更加逼近试验测试的结果，且计算获得的前6阶振型与测试振型一致，可以利用该模型来开展下一步的动刚度预测工作。

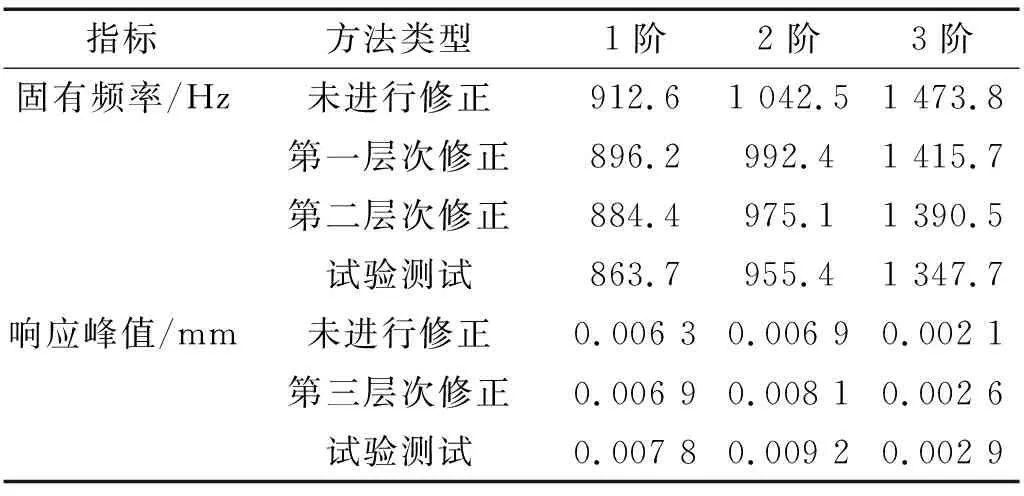
表2 测试和修正前、后计算获得的复合薄壳的前3阶固有频率和振动响应Tab.2 The first three frequencies and vibration responses of FRCS obtained by the measurement and calculation before and after taking multilevel correction technique

同时，图5(a)和图5(b)还分别给出了采用多层次修正技术前、后计算和试验测试获得的复合薄壳响应点1、点2、点3相对于锤击点4的第一阶动刚度曲线，通过图5分析可知，修正后的动刚度曲线与测试曲线相比更加接近。

(a)修正前

(b)修正后图5 采用多层次迭代修正技术前、后通过理论计算与试验测试获得的第一阶动刚度曲线Fig.5 The 1st dynamic stiffness obtained by calculation and experiment before and after using multilevel iterative correction technique

最后，图6还给出了测试获得的响应点1相对于锤击点4的前3阶动刚度曲线。同时，为了便于比较，在相同的锤击点和响应点的前提下，将基于多层次修正技术预测获得的前3阶动刚度曲线一并绘制到图6中。接着，提取图6中曲线对应的前3个波谷值，则可分别获得复合薄壳的第3阶动刚度值，如表3所示。通过与试验结果进行对比可知，基于多层次修正预测获得的纤维增强复合薄壳的动刚度与测试动刚度的误差最大不超过12.2%，处于误差允许的范围内，进而验证了理论预测方法的正确性，利用本文所提出的方法可以较好地实现纤维增强复合薄壳动刚度的预测。

图6 计算和测试获得的纤维增强复合薄壳前3阶动刚度Fig.6 The first three dynamic stiffness of FRCS obtained by calculation and experiment表3 计算和测试获得的纤维增强复合薄壳的前3阶动刚度Tab.3 The first three dynamic stiffness values of FRCS obtained by calculation and experiment